深度学习之优化方法

一.前言

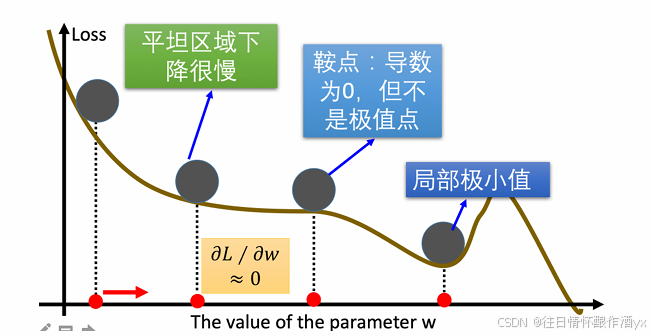
传统的梯度下降优化算法中，可能会碰到以下情况：

碰到平缓区域，梯度值较⼩，参数优化变慢 碰到 “鞍点” ，梯度为 0，参数⽆法优化 碰到局部最⼩值 对于这 些问题, 出现了⼀些对梯度下降算法的优化⽅法，例如：Momentum、AdaGrad、RMSprop、Adam 等.

二.指数加权平均

我们最常⻅的算数平均指的是将所有数加起来除以数的个数，每个数的权重是相同的。加权平均指的是给每 个数赋予不同的权重求得平均数。移动平均数，指的是计算最近邻的 N 个数来获得平均数。

指数移动加权平均则是参考各数值，并且各数值的权重都不同，距离越远的数字对平均数计算的贡献就越⼩ （权重较⼩），距离越近则对平均数的计算贡献就越⼤（权重越⼤）。

⽐如：明天⽓温怎么样，和昨天⽓温有很⼤关系，⽽和⼀个⽉前的⽓温关系就⼩⼀些。

计算公式可以⽤下⾯的式⼦来表示：

 

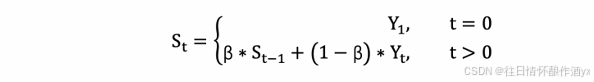
1. St 表示指数加权平均值;

2. Yt 表示 t 时刻的值;

3. β 调节权重系数，该值越⼤平均数越平缓。 

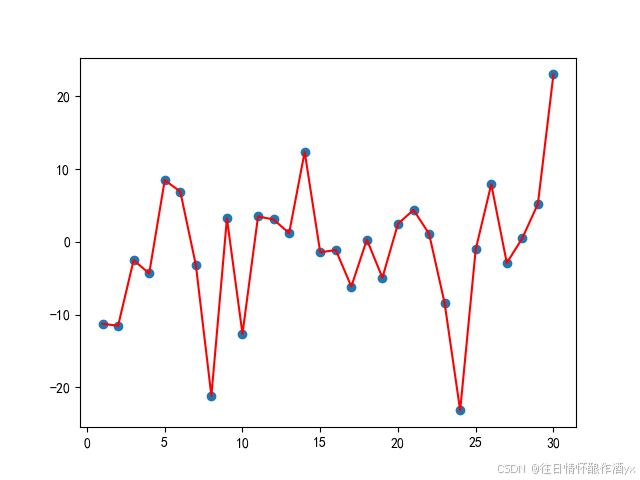
我们接下来通过⼀段代码来看下结果，我们随机产⽣进 30 天的⽓温数据：

import torch
import matplotlib.pyplot as pltELEMENT_NUMBER = 30
# 1. 实际平均温度
def test01():# 固定随机数种⼦torch.manual_seed(0)# 产⽣30天的随机温度temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10print(temperature)# 绘制平均温度days = torch.arange(1, ELEMENT_NUMBER + 1, 1)plt.plot(days, temperature, color='r')plt.scatter(days, temperature)plt.show()# 2. 指数加权平均温度
def test02(beta=0.9):# 固定随机数种⼦torch.manual_seed(0)# 产⽣30天的随机温度temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10print(temperature)exp_weight_avg = []for idx, temp in enumerate(temperature, 1):# 第⼀个元素的的 EWA 值等于⾃身if idx == 1:exp_weight_avg.append(temp)continue# 第⼆个元素的 EWA 值等于上⼀个 EWA 乘以 β + 当前⽓氛乘以 (1-β)new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * tempexp_weight_avg.append(new_temp)days = torch.arange(1, ELEMENT_NUMBER + 1, 1)plt.plot(days, exp_weight_avg, color='r')plt.scatter(days, temperature)plt.show()if __name__ == '__main__':test01()test02(0.5)test02(0.9)

结果展示：

 

 

 

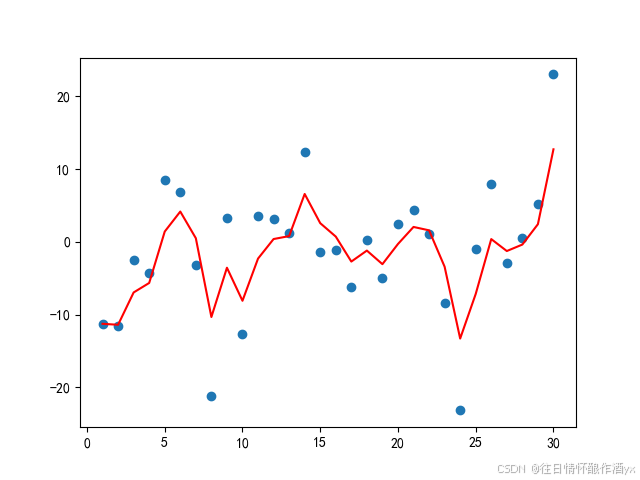
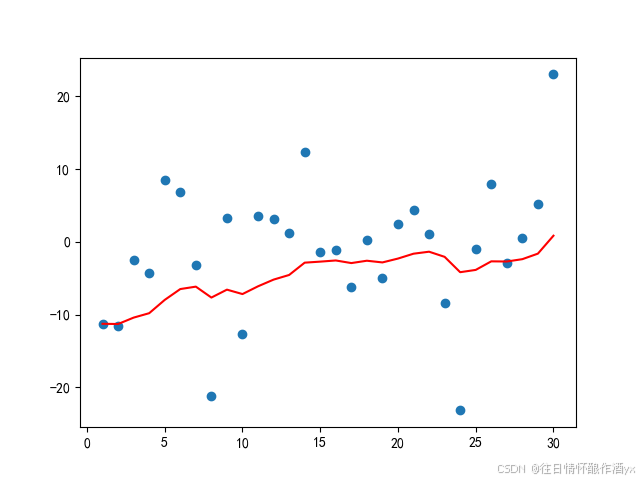
从程序运⾏结果可以看到：

指数加权平均绘制出的⽓氛变化曲线更加平缓; β 的值越⼤，则绘制出的折线越加平缓; β 值⼀般默认都是 0.9.

三.Momentum 

当梯度下降碰到 “峡⾕” 、”平缓”、”鞍点” 区域时, 参数更新速度变慢. Momentum 通过指数加权平均法，累 计历史梯度值，进⾏参数更新，越近的梯度值对当前参数更新的重要性越⼤。

 

梯度计算公式：Dt = β * St-1 + (1- β) * Dt

        1. St-1 表示历史梯度移动加权平均值

        2. wt 表示当前时刻的梯度值

        3. β 为权重系数 

咱们举个例⼦，假设：权重 β 为 0.9，例如：

第⼀次梯度值：s1 = d1 = w1 第⼆次梯度值：s2 = 0.9 + s1 + d2 * 0.1 第三次梯度值：s3 = 0.9 * s2 + d3 * 0.1 第四次梯度值：s4 = 0.9 * s3 + d4 * 0.1

        1. w 表示初始梯度

        2. d 表示当前轮数计算出的梯度值

        3. s 表示历史梯度值

梯度下降公式中梯度的计算，就不再是当前时刻 t 的梯度值，⽽是历史梯度值的指数移动加权平均值。公式修改为：

 

那么，Monmentum 优化⽅法是如何⼀定程度上克服 “平缓”、”鞍点”、”峡⾕” 的问题呢？

 

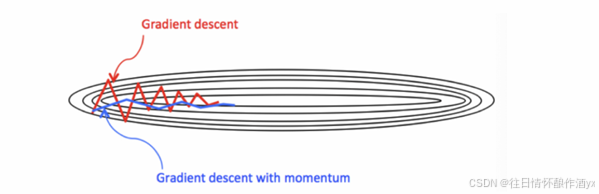
当处于鞍点位置时，由于当前的梯度为 0，参数⽆法更新。但是 Momentum 动量梯度下降算法已经在先前 积累了⼀些梯度值，很有可能使得跨过鞍点。

由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进⽅向，可能会出现震荡，使得训 练时间变⻓。Momentum 使⽤移动加权平均，平滑了梯度的变化，使得前进⽅向更加平缓，有利于加快训 练过程。⼀定程度上有利于降低 “峡⾕” 问题的影响。

峡⾕问题：就是会使得参数更新出现剧烈震荡.

Momentum 算法可以理解为是对梯度值的⼀种调整，我们知道梯度下降算法中还有⼀个很重要的学习率， Momentum 并没有学习率进⾏优化。

四.AdaGrad 

AdaGrad 通过对不同的参数分量使⽤不同的学习率，AdaGrad 的学习率总体会逐渐减⼩，这是因为 AdaGrad 认为：在起初时，我们距离最优⽬标仍较远，可以使⽤较⼤的学习率，加快训练速度，随着迭代次数的增加，学习率逐渐下降。 

其计算步骤如下：

1. 初始化学习率 α、初始化参数 θ、⼩常数 σ = 1e-6

2. 初始化梯度累积变量 s = 0

3. 从训练集中采样 m 个样本的⼩批量，计算梯度 g

4. 累积平⽅梯度 s = s + g ⊙ g，⊙ 表示各个分量相乘

学习率 α 的计算公式如下：

 

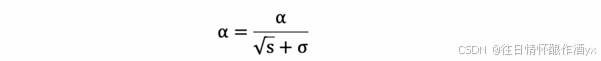
6. 参数更新公式如下：

 

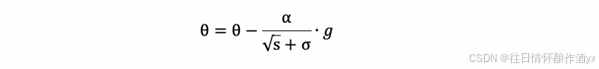
7. 重复 2-7 步骤.

AdaGrad 缺点是可能会使得学习率过早、过量的降低，导致模型训练后期学习率太⼩，较难找到最优解。

五.RMSProp

RMSProp 优化算法是对 AdaGrad 的优化. 最主要的不同是，其使⽤指数移动加权平均梯度替换历史梯度的 平⽅和。其计算过程如下：

1. 初始化学习率 α、初始化参数 θ、⼩常数 σ = 1e-6

2. 初始化参数 θ

3. 初始化梯度累计变量 s

4. 从训练集中采样 m 个样本的⼩批量，计算梯度 g

5. 使⽤指数移动平均累积历史梯度，公式如下：

6. 学习率 α 的计算公式如下：

 

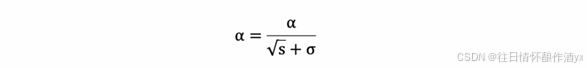
7. 参数更新公式如下：

 

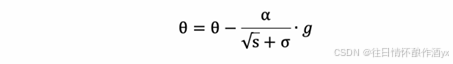
RMSProp 与 AdaGrad 最⼤的区别是对梯度的累积⽅式不同，对于每个梯度分量仍然使⽤不同的学习率。
RMSProp 通过引⼊衰减系数 β，控制历史梯度对历史梯度信息获取的多少. 被证明在神经⽹络⾮凸条件下的 优化更好，学习率衰减更加合理⼀些。

需要注意的是：AdaGrad 和 RMSProp 都是对于不同的参数分量使⽤不同的学习率，如果某个参数分量的 梯度值较⼤，则对应的学习率就会较⼩，如果某个参数分量的梯度较⼩，则对应的学习率就会较⼤⼀些

六.Adam 

Momentum 使⽤指数加权平均计算当前的梯度值、AdaGrad、RMSProp 使⽤⾃适应的学习率，Adam 结合了 Momentum、RMSProp 的优点，使⽤：移动加权平均的梯度和移动加权平均的学习率。使得能够⾃适应学习率的同时，也能够使⽤ Momentum 的优点。 

七.总结 

本⼩节主要学习了常⻅的⼀些对普通梯度下降算法的优化⽅法，主要有 Momentum、AdaGrad、 RMSProp、Adam 等优化⽅法，其中 Momentum 使⽤指数加权平均参考了历史梯度，使得梯度值的变化 更加平缓。AdaGrad 则是针对学习率进⾏了⾃适应优化，由于其实现可能会导致学习率下降过快， RMSProp 对 AdaGrad 的学习率⾃适应计算⽅法进⾏了优化，Adam 则是综合了 Momentum 和 RMSProp 的优点，在很多场景下，Adam 的表示都很不错。