对称二叉树、二叉树直径

101. 对称二叉树 - 力扣（LeetCode）

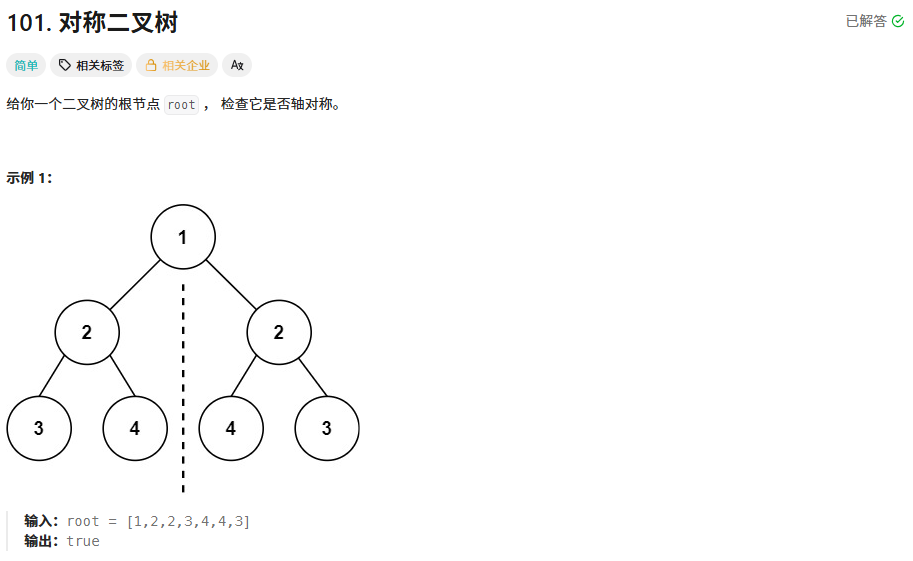
法一：递归。

对于两个对称位置的节点L和R（L在左子树，R在右子树），只有当L的左节点值==R的右节点值且L的右节点值==R的左节点值时，这棵二叉树才有可能对称。另外还需要特判一下nullptr的情况。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:bool check(TreeNode*l,TreeNode*r){if(!l&&!r) return true;if(!l||!r) return false;return l->val==r->val&&check(l->left,r->right)&&check(l->right,r->left);}bool isSymmetric(TreeNode* root) {if(root&&root->left==nullptr&&root->right==nullptr) return true;return check(root->left,root->right);}
};

法二：迭代。如上文所说，对于对称位置的L、R，只有当...时才有可能对称，因此我们只需要将L的左节点与R的右节点匹配、L的右节点和R的左节点匹配。考虑使用队列，取出两次对头匹配即可。本质上还是层序遍历，只不过遍历到一个节点的同时也在遍历它对称位置的节点。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:bool isSymmetric(TreeNode* root) {if(root==nullptr) return true;queue<TreeNode*>que;que.push(root->left);que.push(root->right);while(!que.empty()){TreeNode*lhs=que.front();que.pop();TreeNode*rhs=que.front();que.pop();if(lhs==nullptr&&rhs==nullptr)//有对称的可能{continue;}if(lhs==nullptr&&rhs!=nullptr) return false;if(rhs==nullptr&&lhs!=nullptr) return false;else if(lhs->val!=rhs->val) return false;que.push(lhs->left);que.push(rhs->right);que.push(lhs->right);que.push(rhs->left);}return true;}
};