因果发现PCMCI 算法简述、Tigramite库的简单实践

---

1 PCMCI算法

PCMCI（Peter and Clark Momentary Conditional Independence）算法能够从高维度的时间序列中提取出因果关系图，为后续的预测模型（如图神经网络GNN）提供宝贵的先验知识。其核心思想是结合PC算法（以其发明者Peter Spirtes和Clark Glymour命名）和MCI（瞬时条件独立性）检验，分两阶段高效且准确地识别因果结构。

1.1 与格兰杰因果检验的差别

PCMCI与计量经济学中常见的Granger Causality的差异：

模型	主要思想	适用场景	优点	缺点
PCMCI	两阶段方法：PC算法筛选潜在父节点，MCI进行条件独立性检验。	高维、非线性的时间序列数据。	对高维数据处理能力强，能有效区分直接与间接原因，可处理非线性关系和时间延迟。	对于瞬时（contemporaneous）因果关系的识别能力有限（后续版本如PCMCI+有所改进）。
格兰杰因果检验 (Granger Causality)	如果一个时间序列的过去值能够帮助预测另一个时间序列的未来值，则认为存在格兰杰因果关系。	低维、线性的时间序列数据。	概念简单，易于实现。	仅能捕捉线性关系，容易将间接关系或共同驱动因素误判为直接因果。

1.2 PCMCI的建模步骤

PCMCI 算法可以分为两个主要阶段：PC1 阶段和 MCI 阶段。

1. PC1 阶段（初步筛选潜在父辈）：

这个阶段的目标是为每个变量 $X\_i$ 初步筛选出在过去时间步上可能影响 $X\_i$ 的潜在“父辈”变量。它通过零阶或低阶条件独立性检验来完成。

• 指标计算：在这个阶段，通常使用偏相关系数 (Partial Correlation Coefficient) 或条件互信息 (Conditional Mutual Information) 作为衡量条件独立性的指标。
• 偏相关系数：衡量在控制其他一个或多个变量后，两个变量之间的线性相关强度。例如，$$\begin{gathered} rho\_XY \\ cdotZ \end{gathered}$$ 表示在控制 $Z$ 的情况下 $X$ 和 $Y$ 的相关性。如果这个偏相关系数接近于0，则认为 $X$ 和 $Y$ 在给定 $Z$ 的条件下是独立的。
• 条件互信息：衡量在给定其他变量 $Z$ 的情况下，知道变量 $X$ 对了解变量 $Y$ 的不确定性减少了多少。如果 $I(X;Y|Z)$ 接近于0，则认为 $X$ 和 $Y$ 在给定 $Z$ 的条件下是独立的。条件互信息对于非线性关系也有效。
• 步骤：
  • 1. 对于每个变量 $X\_i$ 和其在所有历史时间步上的其他变量 $$\begin{gathered} X\_j(t- \\ tau) \end{gathered}$$（其中 $tau$ 是时间滞后），计算它们的偏相关系数或条件互信息。
  • 2.基于这些指标，设置一个阈值，将所有相关性低于阈值的边删除。这个过程会剔除掉大部分不相关的边，留下一个包含所有潜在因果链接的宽松图。

2. MCI 阶段 (Momentary Conditional Independence 检验)：
   这个阶段是 PCMCI 区别于标准 PC 算法的关键，它解决了时间序列数据中常见的自相关性和同时因果混淆问题。MCI 会对在 PC1 阶段保留下来的每一条边进行更严格的高阶条件独立性检验。

• 检验方法和指标：MCI 同样使用偏相关系数或条件互信息作为检验指标。但其核心在于条件集的选择。
• 步骤：
  1. 对于在 PC1 阶段保留下来的每一条潜在的因果边 $$\begin{gathered} X\_j(t- \\ tau) \\ toX\_i(t) \end{gathered}$$：
  2. 构建一个条件集 (conditioning set) $S$。这个条件集 $S$ 不仅仅包含 $X\_i(t)$ 和 $$\begin{gathered} X\_j(t- \\ tau) \end{gathered}$$ 以外的所有其他变量的历史值，还会特别包含在当前时间步 $t$ 对 $X\_i$ 和 $X\_j$ 有共同影响的变量（即它们的共同父辈或同时混杂因素）。
  3. 执行 $$\begin{gathered} X\_j(t- \\ tau) \end{gathered}$$ 和 $X\_i(t)$ 在给定条件集 $S$ 下的条件独立性检验。
  4. 如果 $$\begin{gathered} X\_j(t- \\ tau) \end{gathered}$$ 和 $X\_i(t)$ 在给定 $S$ 的条件下是独立的（即检验结果表明它们之间没有显著的条件相关性），则这条边被删除。
  5. 重复此过程，直到没有更多的边可以被删除。
     * 通过这种方式，MCI 能够更有效地消除由于共同原因、同时混淆或时间序列自身的复杂依赖结构（如自回归）导致的虚假因果关系，从而得到一个更接近真实因果结构的图。

1.3 评估因果关系的强度指标

在传统的因果推断文献中，“增量因果效应（Incremental Causal Effects）”通常指轻微干预（如将治疗概率增加10%）所带来的效果。

PCMCI的标准输出并不直接提供这种严格定义下的增量效应。然而，tigramite 库在进行基于线性部分相关性的PCMCI分析时，会输出链接系数（link coefficients）。

• 链接系数的解释：这个系数可以被视为在一个线性模型中，控制了所有其他父辈变量后，原因变量对结果变量的标准化回归系数。它可以被解释为：在其他父辈变量不变的情况下，原因变量每增加一个标准差，结果变量平均会改变多少个标准差。

因此，虽然这不是严格意义上的“增量干预效应”，但这个链接系数确实量化了因果关系的强度和方向，在实践中可以作为评估因果关系“增量”影响力的一个有效代理指标。

1.4 与结构方程模型SEM的差别

特征	PCMCI	结构方程模型 (SEM)
主要功能	因果发现 (Causal Discovery)	模型验证 (Model Verification/Confirmation)
数据类型	主要用于时间序列数据	适用于各种数据类型，通常是横截面数据
模型预设	无需预设完整的因果模型，算法自动发现	需要预先指定详细的理论模型
潜变量	通常不直接处理潜变量	核心功能之一，可以处理潜变量及其测量误差
因果关系	主要识别滞后因果关系	识别观测变量和潜变量之间的直接和间接因果关系
假设	因果马尔可夫条件、忠诚性，通常无同时因果、无隐藏混杂因素	线性关系、多元正态性、无缺失数据、模型正确设定，无隐藏混杂因素，且模型通常是无环的
应用领域	气候学、神经科学、复杂系统分析等	心理学、社会学、经济学、管理学、教育学等

---

简而言之，SEM 更像是你带着一个明确的假设地图去验证是否存在这条路，并且这条路有多宽（路径系数）。
而 PCMCI 则是你不清楚地图，想从错综复杂的道路中发现哪些路是真正连接的，并且是哪个方向连接的，尤其擅长处理时间动态。

选择哪种方法取决于你的研究问题、数据特性以及你对变量之间关系的先验知识。在某些复杂的研究中，甚至可能结合两种方法的思想来获得更全面的理解。

1.5 PCMCI与GNN的结合可能性探索

特性	PCMCI	图神经网络 (GNN)
核心任务	因果发现 (Causal Discovery)	表示学习与预测 (Representation Learning & Prediction)
输入	原始时间序列数据	一个预先定义的图结构和节点特征
输出	一个描述变量间因果关系的有向无环图（DAG）	节点的嵌入表示、图的分类、链接的预测等
目标	解释变量间的底层生成机制	在给定的图结构上学习有效的模式用于预测
方法论	基于统计检验和因果假设	基于神经网络和消息传递机制

简而言之，PCMCI负责回答“为什么”（Why），即发现数据背后的因果结构；而GNN负责利用这个结构来进行更准确的“预测”（What’s next）。

将PCMCI和GNN结合是一种非常强大且符合逻辑的策略，其核心思想是用PCMCI发现的因果图来指导GNN的学习过程。

1. 提取因果图：首先，使用PCMCI算法分析玩家行为的时间序列数据，得到一个因果关系图。这个图的节点代表不同的玩家行为（或玩家本身），有向边代表经过验证的因果关系和时间延迟。
2. 构建GNN的邻接矩阵：将PCMCI输出的因果图转换为一个邻接矩阵 (Adjacency Matrix)。这个邻接矩阵将作为GNN的输入，定义了GNN中节点间的连接关系和消息传递的路径。
3. 作为GNN的先验知识：
   • 固定图结构：最直接的方法是将这个因果邻接矩阵作为GNN的固定图结构。这样，GNN的消息传递就只会在被PCMCI验证为存在因果关系的节点之间进行。这极大地减少了模型的搜索空间，防止了GNN在高度相关但无因果关系的行为之间建立虚假的联系。
   • 作为正则化项：一种更灵活的方法是，不将因果图作为硬性约束，而是作为一个正则化项。例如，可以鼓励GNN学习到的图结构与PCMCI发现的因果图尽可能相似。这允许GNN在因果先验的基础上，发现一些PCMCI可能遗漏的细微关联。

优势：这种结合方式赋予了GNN模型更好的可解释性（因为其结构基于因果发现）和泛化能力。由于模型结构反映了数据的真实生成过程，它对于环境或行为模式的微小变化会更加鲁棒，从而能更准确地预测玩家的下一步行动。

---

2 橄榄球联盟中的因果球员动作预测

这篇Causal Behaviour Modelling for Player Action Prediction in Rugby League Using Graph Neural Networks 论文中提到了研究人员旨在构建因果行为模型来预测玩家的未来行为。
该研究使用的数据分为三种状态（静止/运动/被铲球）、两种环境（进攻/防守）和 12 个感兴趣的动作（例如传球、踢球、断线）。使用 PCMCI 算法，该团队提取了玩家行为的因果图，然后将其用作图神经网络 （GNN） 的先验知识来预测下一个动作。
通过将这种因果结构集成到 GNN 中，该模型获得了比 LSTM 和 Transformers 等标准序列模型更高的准确性和 F1 分数。这种方法将神经网络的预测能力与因果推理的可解释性相结合，既可以进行准确的预测，又可以理解为什么某些作是可能的。

下面贴一个用google gemini的论文解读：

2.1 大致的建模步骤

PCMCI（Peter and Clark Momentary Conditional Independence）算法被用于从时间序列形式的球员行为数据中发现因果图。其建模步骤如下：

1. 数据输入与格式化：将处理后的球员行为特征（如球员位置、速度、持球状态、与球的距离、最近动作类型等）组织成多变量时间序列数据 X={X1,X2,…,Xp}X = \{X_1, X_2, \dots, X_p\}X={X1​,X2​,…,Xp​}，其中 $X_i$ 是一个代表特定行为或状态的时间序列变量。

2. 设置最大时间滞后 (${\tau }_{max}$)：根据橄榄球比赛的节奏和动作发生的时间尺度，设定一个合理的最大时间滞后参数 ${\tau }_{max}$。这意味着算法将在从当前时刻到过去 ${\tau }_{max}$ 个时间步的范围内搜索因果影响。

3. 独立性检验选择 (Selection of Independence Test)：根据数据的统计特性（例如，是否服从高斯分布，关系是否为线性），选择合适的条件独立性检验方法。常见的选择包括：

   • 偏相关 (Partial Correlation, ParCorr)：适用于假设变量之间存在线性高斯关系的场景。
   • 条件互信息 (Conditional Mutual Information, CMI)：适用于捕获非线性关系，对数据分布没有严格的高斯假设。研究者会根据对数据的初步分析选择最合适的检验。

4. PC1 阶段（父辈-子代初步筛选）：

• 目标：为每个变量 $X_i(t)$ 初步识别其在过去时间步的潜在“父辈”变量（即直接影响 $X_i(t)$ 的变量 $X_j(t-\tau )$）。
• 过程：对于所有可能的变量对 $(X_j(t-\tau ),X_i(t))$，以及一个空的或小规模的条件集 $Z$（例如，零阶偏相关），进行条件独立性检验。
• 判定标准：如果 $P(X_j(t-\tau ),X_i(t)|Z)$ 的 P 值低于预设的显著性水平 ${\alpha }_{PC1}$（例如 0.05），则保留这对潜在的因果链接；否则，删除。这一步旨在粗略地剪枝掉大部分不相关的链接，降低后续步骤的计算复杂度。

5. MCI 阶段（瞬时条件独立性检验）：

• 目标：在 PC1 阶段的基础上，对保留下来的每一个潜在链接 $(X_j(t-\tau )\to X_i(t))$ 进行更严格的条件独立性检验，以消除由于共同原因（confounders）或复杂自相关结构引起的虚假关联。
• 过程：对于每一个待检验的链接 $(X_j(t-\tau )\to X_i(t))$，PCMCI 会构建一个精确的条件集 $S$。这个条件集 $S$ 包括：
  • $X_i(t)$ 的已识别的过去父辈（PC1 阶段初步筛选出的，且被认为是真实的父辈）。
  • $X_j(t-\tau )$ 的已识别的过去父辈。
  • 特别是，它会包括在当前时间 $t$ 之前，可能同时影响 $X_i$ 和 $X_j$ 的共同原因。这个机制能够有效处理时间序列中的瞬时混杂和自回归效应。
• 判定标准：如果 $P(X_j(t-\tau ),X_i(t)|S)$ 的 P 值低于预设的显著性水平 ${\alpha }_{MCI}$（例如 0.05），则认为这条因果链接是真实且显著的，并将其添加到最终的因果图中；否则，删除。

6. 输出因果图：最终，PCMCI 输出一个稀疏的有向图 $G=(V,E)$，其中 $V$ 是球员行为特征的集合，$E$ 是表示因果关系的带有时间滞后的有向边。

2.2 PCMCI 与 GNN 结合的建模步骤

本研究将 PCMCI 发现的因果图作为 GNN 的核心输入结构，从而使 GNN 的学习过程能够受益于因果知识。

1. 因果图到 GNN 邻接矩阵的转化 (Causal Graph to GNN Adjacency Matrix)：

• PCMCI 发现的因果图 $G$ 被转化为 GNN 所需的邻接矩阵 $A$。
• 如果存在从行为特征 $X_j$ (在时间 $t-\tau$) 到行为特征 $X_i$ (在时间 $t$) 的因果链接，则邻接矩阵中的相应元素 $A_{ij}$ 被赋值为 1（或基于因果强度进行加权）；否则为 0。
• 值得注意的是，这里的图是有向图，意味着信息流是单向的，这与因果关系的本质一致。考虑到时间滞后，可以在 GNN 中设计特定的层来处理不同滞后下的信息聚合，或者简单地将不同滞后的父辈视为不同的“邻居类型”。

2. 节点特征提取 (Node Feature Extraction)：

• 除了图结构，GNN 还需要节点特征。这些特征是每个球员行为特征在特定时间步的瞬时状态表示。例如，对于一个代表“持球球员位置”的节点，其特征可以是其坐标 (x, y)。
• 论文可能将多种球员行为特征（如位置、速度、动作类型、是否持球等）组合成每个时间步的节点特征向量。

3. GNN 模型架构设计 (GNN Model Architecture Design)：

• 选择合适的 GNN 架构，如图卷积网络 (GCN)、图注意力网络 (GAT) 或时空图神经网络 (STGNN)。考虑到数据的时间序列性质和图的动态性，STGNN 可能是更自然的选择，因为它能同时处理空间（因果图）和时间维度的信息。
• GNN 层通过聚合来自邻居节点（即因果父辈）的信息来更新每个节点的特征表示。这种聚合过程是根据因果图的连接进行的。

4. 预测层与损失函数 (Prediction Layer and Loss Function)：

• GNN 学习到每个球员行为的高维嵌入向量。
• 这些嵌入向量被输入到一个分类层（例如，一个或多个全连接层加上 Softmax 激活函数），以预测球员在下一个时间步将执行的动作类别（如“传球”、“跑动”、“踢球”、“防守”等）。
• 使用交叉熵损失函数或其他适用于多分类任务的损失函数进行模型训练。

5. 模型训练与评估 (Model Training and Evaluation)：

• 使用历史比赛数据对 GNN 模型进行端到端训练。
• 评估模型在预测球员下一个动作上的准确性、F1 分数等指标，并与基线模型进行比较，以证明因果建模的有效性。

---

3 PCMCI的Python实现：Tigramite

3.1 Tigramite介绍

github地址：https://github.com/jakobrunge/tigramite
doc地址：https://jakobrunge.github.io/tigramite/
tutorials地址：https://github.com/jakobrunge/tigramite/tree/master/tutorials/

Tigramite是一个因果时间序列分析Python软件包。它允许从高维时间序列数据集（因果发现）中有效估计因果图，并使用这些图表进行健壮的预测以及直接，总和介导效应的估计和预测。
因果发现基于线性以及适用于离散或连续值时间序列的非参数条件独立性测试。还包括用于结果的高质量图的功能。请根据您使用的方法引用以下论文：
Overview: Runge, J., Gerhardus, A., Varando, G. et al. Causal inference for time series. Nat Rev Earth Environ (2023). https://doi.org/10.1038/s43017-023-00431-y

Tigramite提供了几种可因果发现方法，可以在不同的假设集中使用。应用程序始终由一种方法和选择的条件独立测试组成，例如PCMCIPLUS与Parcorr一起。以下两个表概述了所涉及的假设：

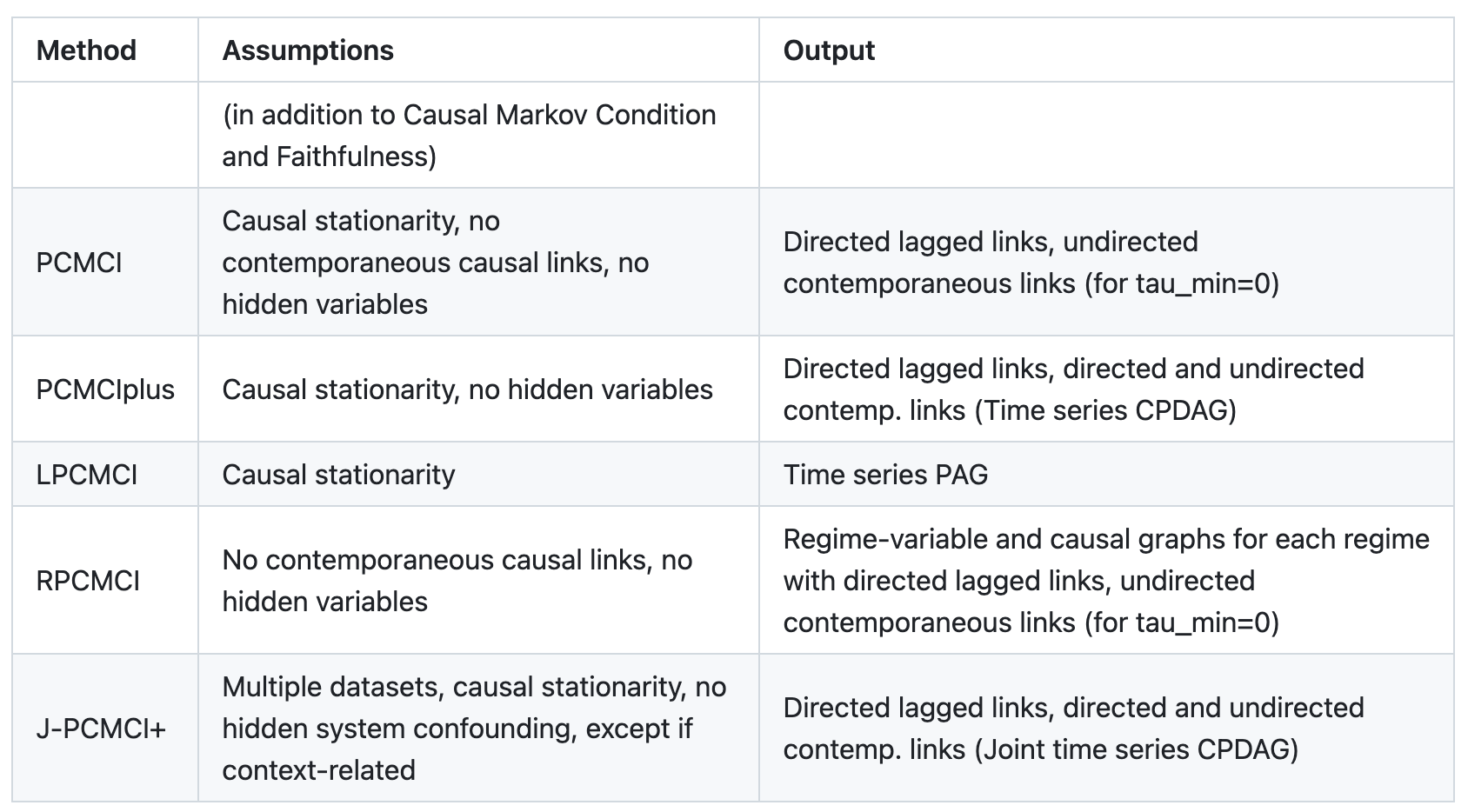
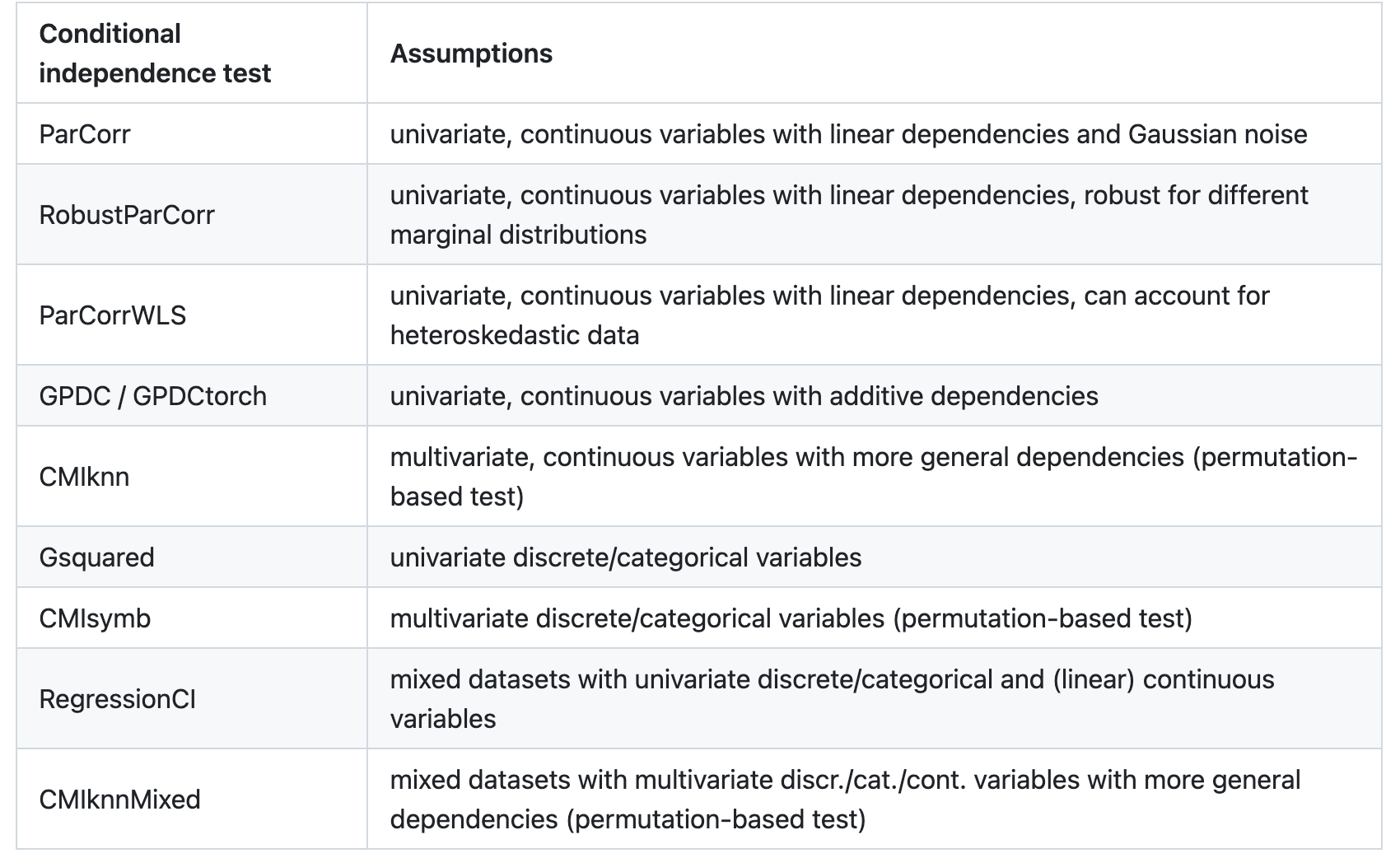
3.2 代码案例

笔者看到已经有博主把一些代码案例进行翻译：
tigramite教程（六）使用TIGRAMITE 进行因果发现
我就不重复劳动了，这里快速验证一个笔者自己设想的案例
使用PCMCI 以王者荣耀游戏中的场景举例

安装：

!pip install tigramite matplotlib networkx

代码大概流程：

• 伪造一个数据集
• 假设有三个动作：进攻（Attack）、闪现逃跑（Flash_escape）、回城逃跑（Recall_escape）
• 关系预设：假设Attack影响Flash_escape, Recall_escape；Enemy_HP影响Attack和Flash_escape；进攻动作受前一时刻的进攻和敌方血量影响
• 构建Tigramite对象 + 设置最大延迟（例如延迟为2步）
• 预测下一个动作可能性（以进攻为例），使用过去两步数据预测下一步Attack

# PCMCI模型在王者荣耀场景的应用示例
# 2. 导入相关库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tigramite import data_processing as pp
from tigramite import plotting as tp
from tigramite.pcmci import PCMCI
from tigramite.independence_tests.parcorr import ParCorr# 3. 模拟王者荣耀玩家行为数据
# 假设有三个动作：进攻（Attack）、闪现逃跑（Flash_escape）、回城逃跑（Recall_escape）
np.random.seed(42)
T = 500  # 时间步数
# 进攻动作受前一时刻的进攻和敌方血量影响
Attack = np.zeros(T)
Flash_escape = np.zeros(T)
Recall_escape = np.zeros(T)# 模拟敌方血量
Enemy_HP = 100 - np.cumsum(np.random.normal(0.2, 0.5, T))
Enemy_HP = np.clip(Enemy_HP, 0, 100)for t in range(1, T):# 进攻概率提高：如果上一时刻在进攻，且敌方血量较高Attack[t] = np.random.binomial(1, 0.3 + 0.2*Attack[t-1] + 0.2*(Enemy_HP[t-1] > 30))# 闪现逃跑：如果上一时刻进攻但敌方血量低，逃跑概率高Flash_escape[t] = np.random.binomial(1, 0.1 + 0.3*Attack[t-1]*(Enemy_HP[t-1] < 20))# 回城逃跑：如果连续两步未进攻且上一时刻未闪现Recall_escape[t] = np.random.binomial(1, 0.05 + 0.2*((Attack[t-1]==0)&(Attack[t-2]==0)&(Flash_escape[t-1]==0)))# 构造DataFrame
data_df = pd.DataFrame({"Attack": Attack,"Flash_escape": Flash_escape,"Recall_escape": Recall_escape,"Enemy_HP": Enemy_HP,
})# 4. 数据清洗
# 检查缺失值并填充
data_df.fillna(0, inplace=True)# 5. 因果关系预设说明
# 假设Attack影响Flash_escape, Recall_escape；Enemy_HP影响Attack和Flash_escape# 6. Tigramite对象生成
var_names = list(data_df.columns)
data = pp.DataFrame(data_df.values, var_names=var_names)# 7. PCMCI建模
# 设置最大延迟（例如延迟为2步）
pcmci = PCMCI(dataframe=data,cond_ind_test=ParCorr(),  # 使用偏相关检验verbosity=1
)
results = pcmci.run_pcmci(tau_max=2,  # 最大时间延迟pc_alpha=0.05  # 初筛显著性水平
)# 8. 结果可视化：绘制因果图
# 只显示显著的因果关系
tp.plot_graph(results['graph'],val_matrix=results['val_matrix'],#link_matrix=results['link_matrix'],var_names=var_names,#alpha_level=0.05,figsize=(8,6)
)
plt.title("王者荣耀玩家行为PCMCI因果图")
plt.show()# 9. 评估模型：输出显著因果关系表
print("显著因果关系：")
for i, src in enumerate(var_names):for j, tgt in enumerate(var_names):for tau in range(1,3):p = results['p_matrix'][i, j, tau]if p < 0.05:print(f"{src}(t-{tau}) → {tgt}(t) | p-value={p:.3f}")# 10. 预测下一个动作可能性（以进攻为例）
# 构建简单的因果推断预测器（以Attack为目标）
from sklearn.linear_model import LogisticRegression# 使用过去两步数据预测下一步Attack
feature_cols = ['Attack', 'Flash_escape', 'Recall_escape', 'Enemy_HP']
X = []
y = []
for t in range(2, T-1):# 拼接过去两步的数据作为特征feats = np.concatenate([data_df.loc[t-1, feature_cols], data_df.loc[t-2, feature_cols]])X.append(feats)y.append(data_df.loc[t, 'Attack'])
X = np.array(X)
y = np.array(y)# 训练预测器
clf = LogisticRegression()
clf.fit(X, y)# 预测最后一步Attack的概率
last_feats = np.concatenate([data_df.loc[T-2, feature_cols], data_df.loc[T-3, feature_cols]]).reshape(1, -1)
prob = clf.predict_proba(last_feats)[0,1]
print(f"\n预测下一步进攻动作概率: {prob:.2f}")

数据集是这样的：

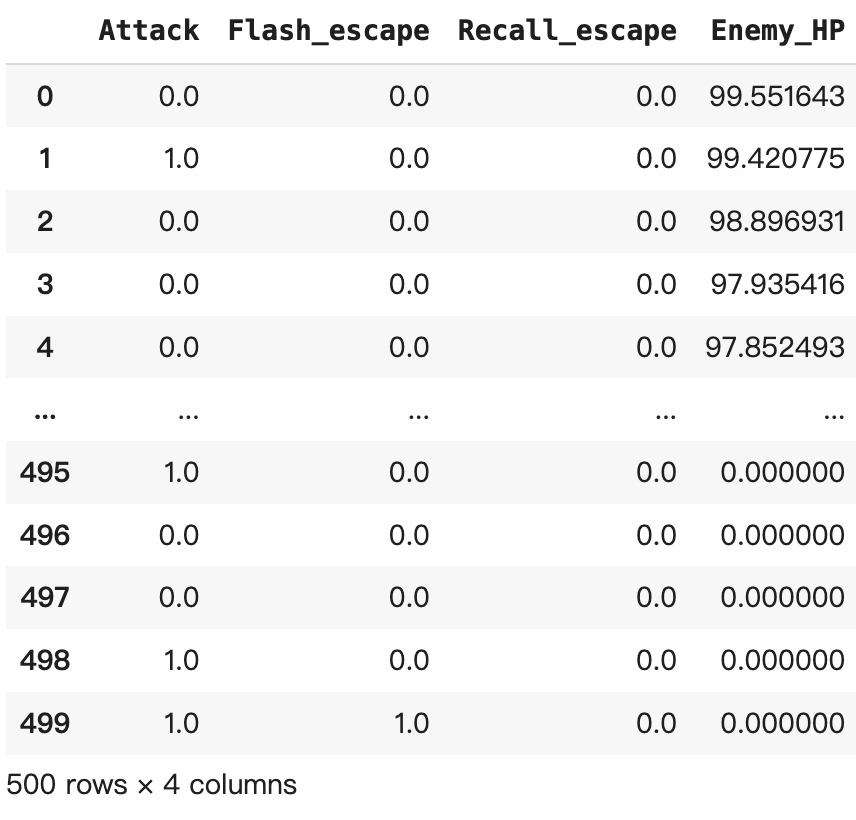
生成的因果图：

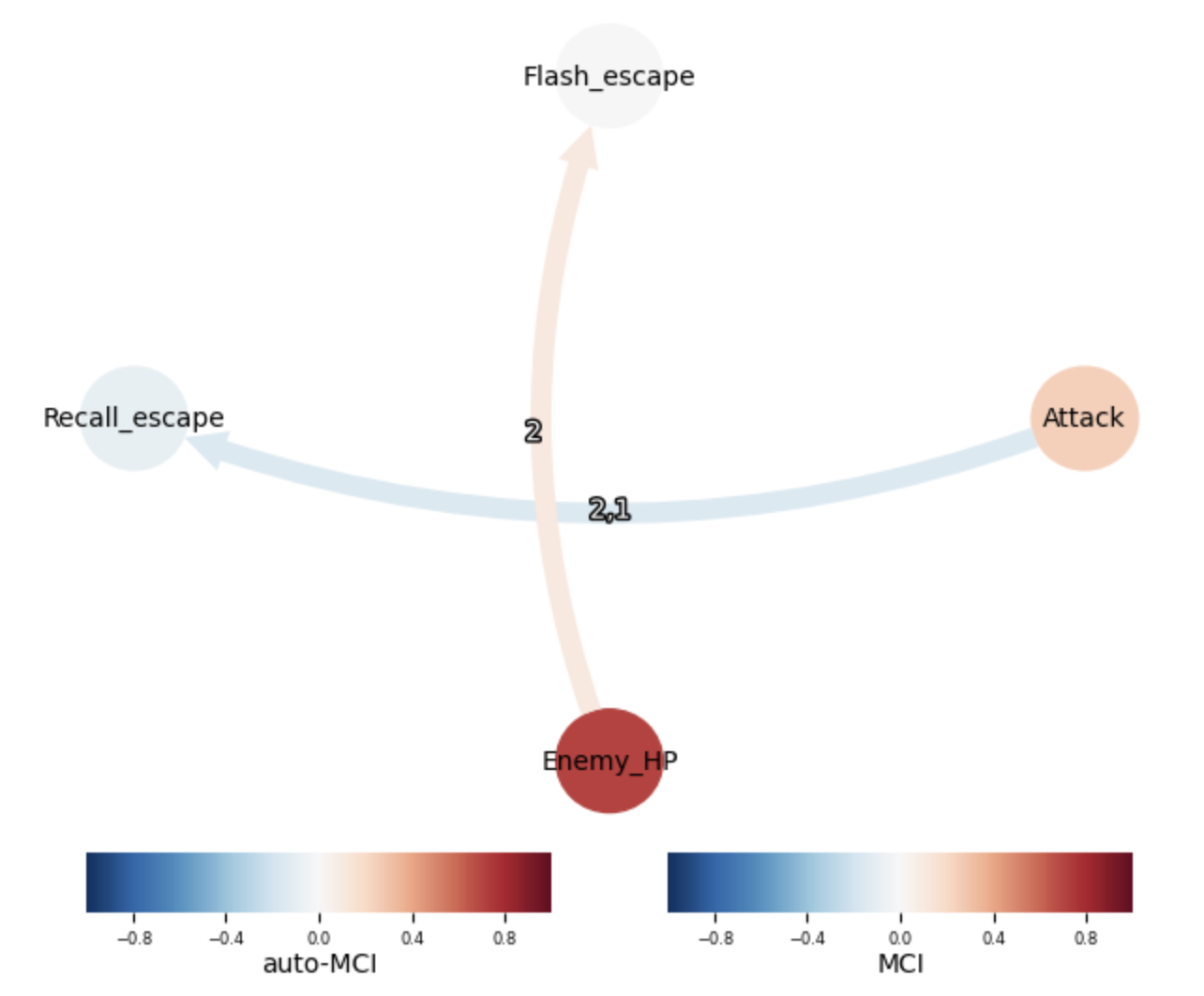
显著因果关系：

Attack(t-1) → Attack(t) | p-value=0.000
Attack(t-1) → Recall_escape(t) | p-value=0.005
Attack(t-2) → Recall_escape(t) | p-value=0.001
Recall_escape(t-2) → Recall_escape(t) | p-value=0.042
Enemy_HP(t-2) → Flash_escape(t) | p-value=0.020
Enemy_HP(t-1) → Enemy_HP(t) | p-value=0.000

预测动作：

预测下一步进攻动作概率: 0.60