图示+例子 深入理解 前向反向传播

详细解析神经网络中的前向传播、反向传播以及计算图的原理与应用，帮助你更好地理解深度学习模型是如何优化和学习的。

1 前向传播：计算神经网络输出

前向传播是神经网络训练中的基础过程，它将输入数据通过神经网络的各层计算，最终得到模型的预测结果。其过程可以通过以下几步进行理解：

1. 输入数据传递：从输入层到隐藏层进行计算。假设输入为 $x\in {\mathbb{R}}^d$，权重为 $W^{(1)}\in {\mathbb{R}}^{h\times d}$，计算得到中间变量 $z=W^{(1)}x$。

2. 激活函数处理：将中间变量 $z$ 通过激活函数 $\varphi$ 处理，得到隐藏层的激活向量 $h=\varphi (z)$。

3. 输出层计算：输出层将隐藏层的激活向量 $h$ 乘以权重 $W^{(2)}\in {\mathbb{R}}^{q\times h}$，得到最终的输出 $o=W^{(2)}h$。

4. 损失计算：通过损失函数 $l(o,y)$ 计算网络输出 $o$ 与真实标签 $y$ 的差距。

通过这些步骤，网络能够根据输入数据给出预测结果。

2 反向传播：更新神经网络权重

反向传播是神经网络训练中的关键过程，它计算损失函数相对于模型权重的梯度，并通过这些梯度来更新权重。反向传播的基本原理基于微积分中的链式法则，具体步骤如下：

1. 目标函数的梯度：首先，计算目标函数相对于损失项 $L$ 和正则化项 $s$ 的梯度。

2. 梯度传递：从输出层开始，逐层通过链式法则传递梯度，依次计算每层的参数梯度。

3. 更新权重：根据梯度下降算法，用计算出的梯度来更新每层的权重。

通过反向传播，神经网络能够在训练过程中不断调整参数，最小化损失函数，进而优化模型。

3 使用计算图理解前向和反向传播

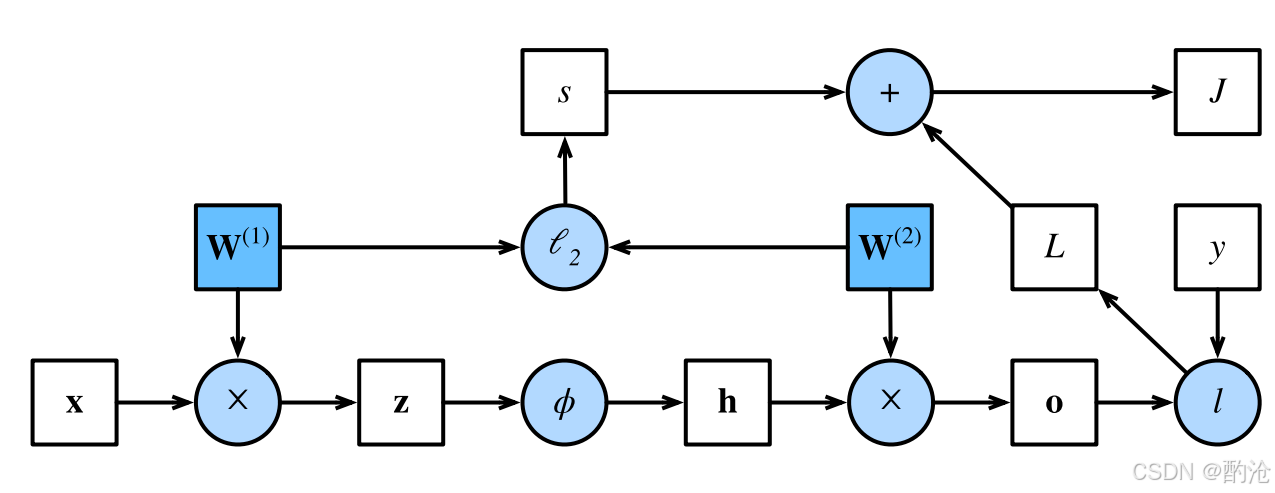
📊 这是简单神经网络的计算图，计算图是前向传播和反向传播的可视化工具，它展示了神经网络中各个变量和操作符之间的依赖关系。白色方块是张量变量，例如 x、z、h、o、L、s、J、y 。蓝色方块是可训练参数，例如W1, W2。 浅蓝圆圈是操作符，例如“×”矩阵乘、“ϕ”激活、“ℓ₂”正则、“+”求和、“l”损失

通过计算图，我们可以更直观地理解网络的运算流程。箭头方向 = 数据流向

• 横向：沿网络层次从左→右传递数值
• 纵向（向上）：把正则项与损失一路汇聚到目标 J

1. 输入 → 隐藏层线性变换
   $z=W^{(1)}x$ (× 节点)
2. 激活
   $h=\phi (z)$ (ϕ 节点，ReLU/σ 等)
3. 隐藏 → 输出层线性变换
   $o=W^{(2)}h$ (× 节点)
4. 计算数据损失
   $L=l(o,y)$ (l 节点，交叉熵/均方误差等)
5. 计算 L2 正则
   $s=\frac{\lambda }{2}(\Vert W^{(1)}{\Vert }_F^2+\Vert W^{(2)}{\Vert }_F^2)$ (ℓ₂ 节点)
6. 合并目标函数
   $J=L+s$ (+ 节点)

• “数据损失 L” 和 “正则损失 s” 是两股并行支流；在最后 + 号处才汇合成全局目标 J。

• J 标量输出（右上角的白方块）意味着整张图最终只流出一个数——训练要最小化的目标函数。

步骤	目标	上游梯度	局部梯度	全局梯度
① 汇合损失	$J=L+s$	1	$\partial J/\partial L=1,\partial J/\partial s=1$	——
② 到输出层	$o=W^{(2)}h$	$\partial J/\partial o$	$h^{\top }$	$\partial J/\partial W^{(2)}=\partial J/\partial o{h}^{\top }$
③ 过隐藏层	$h=\varphi (z)$	$\partial J/\partial h$	$\varphi \prime (z)$	$\partial J/\partial z=(\partial J/\partial h)\odot \varphi \prime (z)$
④ 回到输入侧权重	$z=W^{(1)}x$	$\partial J/\partial z$	$x^{\top }$	$\partial J/\partial W^{(1)}=\partial J/\partial z{x}^{\top }$

📊 每一行就是“上游梯度 × 局部梯度 = 本层梯度”，和水管倒流一样简单；正则项只是在②、④行把 λW 的额外水流并进来。

反向传播如何在计算图上“倒流”？

• 起点：从最顶端标量 J 的导数 $\partial J/\partial J=1$ 开始。

• 沿每条边反向走：到达一个操作圆圈时，把当前“上游梯度”乘以该节点的局部导数，再沿着所有输入边分发到更下游。

  • 例如到 + 节点：梯度在两条输入边 (L, s) 上各复用一份；
  • 到 ℓ₂ 节点：局部导数是 $\lambda W^{(i)}$，立刻得到正则对权重的梯度；
  • 到 × 节点：需要用矩阵微积分结果，把梯度分别乘以另一侧输入的转置。

• 终点：落到蓝色权重方块 W1, W2时，累积好的 $\partial J/\partial W^{(i)}$ 交给优化器（SGD、Adam…）进行梯度更新。

一句话本质：反向传播就是链式法则的向量化实现，而计算图把“谁乘谁”与“何时乘”全都形象化了。

4 最简单的例子来演示整套流程

名称	数值	说明
输入 $x$	2.0	例如房子的面积
真实标签 $y$	3.0	真实房价（归一化后）
权重 $w$	0.5	初始猜测斜率
偏置 $b$	0.1	初始猜测截距
损失函数 $L$	$\frac{1}{2}(\hat{y}-y{)}^2$	取 MSE 的 $\frac{1}{2}$ 形式，便于推导

📊 用一条直线拟合一个点（再小不过的神经网络）来演示整套流程。设定场景与初始数值，模型只有 1 个权重 w 和 1 个偏置 b，目标是让预测值尽量接近真实标签 y。

前向传播：先算出预测值和损失

1. 线性计算
   $$\hat{y}=w\cdot x+b=0.5\times 2+0.1=1.1$$
2. 损失计算
   $$L=\frac{1}{2}(\hat{y}-y{)}^2=\frac{1}{2}(1.1-3{)}^2=\frac{1}{2}\times 3.61=1.805$$

反向传播：再算出梯度，用来修正 w、b
从损失往回一步步链式求导：

量	推导	结果（数值）
$\frac{\partial L}{\partial \hat{y}}$	$(\hat{y}-y)$	$-1.9$
$\frac{\partial \hat{y}}{\partial w}$	$x$	$2.0$
$\frac{\partial \hat{y}}{\partial b}$	$1$	$1$
最终梯度
$\frac{\partial L}{\partial w}$	$\frac{\partial L}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial w}$	$(-1.9)\times 2=-3.8$
$\frac{\partial L}{\partial b}$	$\frac{\partial L}{\partial \hat{y}}\cdot \frac{\partial \hat{y}}{\partial b}$	$-1.9)\times 1=-1.9$

📊 误差 $-1.9$ 说明预测低了。权重梯度 -3.8：面积系数 w 应往 大方向 调（负号＋学习率会变成加）。偏置梯度 -1.9：整体截距也应往上调。

参数更新

以学习率 $\eta =0.1$ 为例）

$$w_{\text{new}}=w-\eta \frac{\partial L}{\partial w}=0.5-0.1(-3.8)=0.88$$

$$b_{\text{new}}=b-\eta \frac{\partial L}{\partial b}=0.1-0.1(-1.9)=0.29$$

经过更新后，新的权重w应该从0.5改为0.88，新的偏置b应该从0.1改为0.29

$$b_{\text{new}}=b-\eta \frac{\partial L}{\partial b}=0.1-0.1(-1.9)=0.29$$

经过更新后，新的权重w应该从0.5改为0.88，新的偏置b应该从0.1改为0.29

这样就完成一次 “前向算输出 → 反向算梯度 → 调整参数” 的完整迭代。