薄板样条（TPS, Thin Plate Spline）数学原理推导

1. TPS 的问题描述

想象一块薄钢板，桌上钉了 $N$ 根钉子，已知：

1、钉子 $i$ 的位置：
$${\mathbf{x}}_i=(x_i,y_i)$$

2、每根钉子想要被拉到高度：
$$z_i$$

目标：找出一个光滑的曲面 $f(x,y)$，经过所有钉子，且尽量平滑。

2. 建立TPS模型

2.1 弯曲能量函数

二维 TPS 的弯曲能量（这里不做推导，你只需要知道这个方程表示的是薄板的弯曲程度对应的能量E）：
$$E=\iint \left[{\left(\frac{{\partial }^{2}f}{\partial x^2}\right)}^2+2{\left(\frac{{\partial }^{2}f}{\partial x\partial y}\right)}^2+{\left(\frac{{\partial }^{2}f}{\partial y^2}\right)}^2\right]dxdy$$

物理含义：板子越弯曲，能量越大。

2.2 目标函数

我们想解这个优化问题，最小化以下目标：

（1）拟合所有钉子高度
$$f(x_i,y_i)=z_i$$
（2） 保证曲面最光滑 → 最小化弯曲能

所以可以写成如下形式：
$$\text{Loss}=\sum _{i=1}^N{\left(f(x_i,y_i)-z_i\right)}^2+\lambda \cdot E（公式1）$$

• 第一项：拟合误差
• 第二项：弯曲能量
• $\lambda$：平滑参数

带入E,Loss完整形式为：
$$Loss=\min \left[\sum _{i=1}^N{\left(f(x_i,y_i)-z_i\right)}^2+\lambda \cdot \iint \left(f_{xx}^2+2f_{xy}^2+f_{yy}^2\right)dxdy\right]（公式2）$$
这是一个变分法问题。

• 第一个部分 → 拟合数据（这部分很好理解，就是最小二乘法能量最小）
• 第二个部分 → 惩罚曲面弯曲（为什么是这样？请看附录1）

2.3 进一步简化表达形式

目的：原有表达形式是刚性和非刚性变化混在一起，难以对每一部分单独划分，因此需要将其拆解为仿射变化和非刚性变化，仿射变换只改变平移、缩放；非刚性负责旋转、弯曲等变换。

通过变分法 + 双调和方程，可以将公式1写为（至于如何化简的，感兴趣去看变分法，这里也不推导了）：
$$f(x,y)=\text{Affine}+\sum w_i\cdot U(r)$$
那么公式2即可写为：
$$f(x,y)=a_1\cdot x+a_2\cdot y+a_3+\sum _{j=1}^N{w}_{j}U\left(\Vert (x,y)-(x_j,y_j)\Vert \right)$$
其中：

• $a_1,a_2,a_3$：仿射项 (表示平面或倾斜面)

• $w_j$：权重，表示每根钉子对弯曲的贡献

• $U(r)$：核函数：
  $$U(r)=r^2\log r，其中r=\Vert (x,y)-(x_j,y_j)\Vert$$

3. 建立方程

3.1 约束条件1

因为每根钉子都在平面$f(x,y)$，因此要求：
$$f(x_i,y_i)=z_i$$
对 $i=1,\dots ,N$ 都成立。
即：$$f(x_i,y_i)=a_1{x}_i+a_2{y}_i+a_3+\sum _{j=1}^N{w}_j\cdot U\left(\Vert (x_i,y_i)-(x_j,y_j)\Vert \right)$$

3.2 约束条件2

非刚性部分不能有刚性的变化量，所有的刚性变化都必须由仿射量提供，这就是边界条件，因此TPS 必须满足

$$\begin{gathered} \sum _{j=1}^N{w}_j=0, \\ \sum _{j=1}^N{w}_j\cdot x_j=0, \\ \sum _{j=1}^N{w}_j\cdot y_j=0 \end{gathered}$$
意思：弯曲部分 不能产生平移或旋转，这些由仿射项负责。

3.3 矩阵形式

(1) 第一部分： $a_1{x}_i+a_2{y}_i+a_3$为仿射项

定义仿射矩阵 $P$：
$$P=\left[\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ ⋮& ⋮& ⋮\\ x_N& y_N& 1\end{array}\right]$$
定义核矩阵 $c=[a1,a2,a3{]}^T$

$a_1{x}_i+a_2{y}_i+a_3$仿射项可记作写为：
$$Pc=\left[\begin{array}{ccc}{x}_1& y_1& 1\\ x_2& y_2& 1\\ ⋮& ⋮& ⋮\\ x_N& y_N& 1\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_N\end{array}\right]$$
（2）第二部分：${\sum }_{j=1}^N{w}_j\cdot U(\Vert (x_i,y_i)-(x_j,y_j)\Vert )$为非刚性变换

定义核矩阵 $K$：
$$K_{ij}=U(\Vert (x_i,y_i)-(x_j,y_j)\Vert )$$
定义核矩阵 $W=[w_1,w_2,\dots ,w_N{]}^T$

那么，${\sum }_{j=1}^N{w}_j\cdot U(\Vert (x_i,y_i)-(x_j,y_j)\Vert )$非刚性项则可以记作：
$$KW=\left[\begin{array}{c}{K}_{11},K_{12},\dots K_{ij}\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_N\end{array}\right]$$
（3）还差一个是边界条件

$$P^T\cdot W=\left[\begin{array}{ccc}{x}_1& x_2& x_3\\ y_1& y_2& y_3\\ ⋮& ⋮& ⋮\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_N\end{array}\right]=0$$

(4) 一二部分相加（仿射+非刚性）：
$$f(x_i,y_i)=a_1{x}_i+a_2{y}_i+a_3+\sum _{j=1}^N{w}_j\cdot U\left(\Vert (x_i,y_i)-(x_j,y_j)\Vert \right)$$
就可以记作：
$$Z=Pc+KW$$
边界部分：

$$P^T\cdot W=0$$

(5) 约束1和约束2写成矩阵方程：
$$\left[\begin{array}{cc}K& P\\ P^T& 0\end{array}\right]\cdot \left[\begin{array}{c}W\\ c\end{array}\right]=\left[\begin{array}{c}Z\\ 0\end{array}\right]$$

4 代码实现

import numpy as np
import matplotlib.pyplot as plt# ------------------------
# 定义控制点
# ------------------------# 控制点坐标 (x, y)
points = np.array([[0, 0],[1, 0],[0, 1],[2, 1],[1, 2],[0, 2]
])# 每个控制点想要达到的高度
heights = np.array([0, 2, 1, 3, 1, 0])N = points.shape[0]# ------------------------
# 计算核矩阵 K
# ------------------------def U(r):# 为避免 log(0)，加一个极小值r[r == 0] = 1e-20return r**2 * np.log(r)# pairwise distance matrix
dist_matrix = np.linalg.norm(points[:, np.newaxis, :] - points[np.newaxis, :, :],axis=2
)K = U(dist_matrix)# ------------------------
# 构造 P 矩阵
# ------------------------# 对每个点，P = [x, y, 1]
P = np.hstack((points,np.ones((N, 1))
))# ------------------------
# 拼接完整矩阵
# ------------------------# 大矩阵 A
A_upper = np.hstack((K, P))
A_lower = np.hstack((P.T, np.zeros((3,3))))
A = np.vstack((A_upper, A_lower))# 构造右边的向量
Y = np.concatenate([heights, np.zeros(3)])# ------------------------
# 解方程
# ------------------------params = np.linalg.solve(A, Y)# 提取结果
W = params[:N]
a1, a2, a3 = params[N:]print("权重 W =", W)
print("仿射项 = ", [a1, a2, a3])# ------------------------
# 计算网格上的值
# ------------------------# 建一个网格
grid_x, grid_y = np.meshgrid(np.linspace(-0.5, 3, 50),np.linspace(-0.5, 3, 50)
)grid_points = np.vstack((grid_x.ravel(),grid_y.ravel()
)).T# 计算每个网格点到所有控制点的距离
dists_to_points = np.linalg.norm(grid_points[:, np.newaxis, :] - points[np.newaxis, :, :],axis=2
)U_values = U(dists_to_points)  # shape = (M, N)# 弯曲部分
bending_part = U_values @ W# 仿射部分
affine_part = a1 * grid_points[:,0] + a2 * grid_points[:,1] + a3# 总 TPS
grid_heights = bending_part + affine_part
grid_heights = grid_heights.reshape(grid_x.shape)# ------------------------
# 绘制曲面
# ------------------------fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(grid_x, grid_y, grid_heights, cmap='viridis', alpha=0.8)# 绘制控制点
ax.scatter(points[:,0], points[:,1], heights, color='r', s=50, label='Control Points')ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Height')
ax.set_title('TPS')
ax.legend()
plt.show()

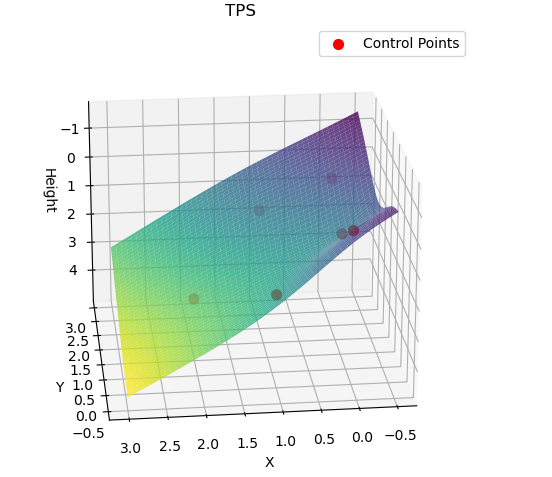
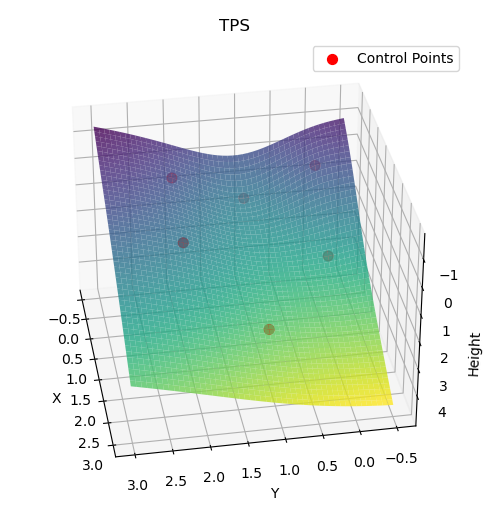
运行结果

权重 W = [-5.6051292e-01 1.9983916e-01 7.2134752e-01 8.2778442e-17
-1.9983916e-01 -1.6083460e-01]
仿射项 = [1.451205059304602, -0.25000000000000006, 1.2499999999999998]