「大模型应用」(2)RAG的检索与rerank

0. 基础内容

我们先来介绍几种检索方式，在 RAG（Retrieval-Augmented Generation，检索增强生成）框架中，稀疏检索器（Sparse Retriever） 和 密集检索器（Dense Retriever） 是两种核心的文档检索方式，它们的主要作用是：

从海量知识库中找出与用户输入相关的文档，供语言模型参考生成回答。

---

一、稀疏检索器（Sparse Retriever）

✅ 基本原理

稀疏检索器通常基于 传统的倒排索引（Inverted Index） 和 词频统计特征，（特征值获取也可以使用学习的手段）比如：

• TF-IDF（Term Frequency-Inverse Document Frequency）
• BM25（Best Matching 25）

其本质是：

• 将文本表示为一个 高维稀疏向量（维度=词汇表大小）
• 计算查询和文档之间的词重叠与权重相似度

✅ 特点

特性	说明
表达方式	单词级稀疏表示（one-hot 或 TF-IDF）
索引方式	倒排索引，效率高
检索速度	快，适合大规模文档
训练需求	无需训练（规则或简单统计）
表达能力	依赖关键词，不能捕捉语义相似（如“car”和“automobile”不会匹配）

✅ 常用工具

• Elasticsearch
• Lucene
• Whoosh
• sklearn.TfidfVectorizer + cosine_similarity

具体步骤：

第一步：文本编码为 token 向量

我们使用一个 Transformer 编码器（如 XLM-RoBERTa、BERT 等）将文本变为 token 级别的隐藏表示。

对于一个输入文档 $d=[t_1,t_2,\dots ,t_n]$，编码器输出：

$${\mathbf{H}}_d=[h_1,h_2,\dots ,h_n]\in {\mathbb{R}}^{n\times d}$$

其中 $h_i\in {\mathbb{R}}^d$ 是第 $i$ 个 token 的表示向量。

第二步：对每个 token 输出词权重（可学习）

用一个额外的线性头来学习每个词的重要性（也可以使用静态的方式如TF-IDF 是静态、规则计算的，而模这里是 基于上下文、可学习的、更灵活的语义权重。）：

$$w_i=\text{ReLU}(W{h}_i+b)\in \mathbb{R}$$

其中：

• $W\in {\mathbb{R}}^{1\times d}$：投影矩阵
• $b\in \mathbb{R}$：偏置
• $w_i$：第 $i$ 个 token 的 scalar 权重分数
• ReLU 保证非负性（符合稀疏表示）

第三步：生成稀疏向量（Sparse Representation）

我们将每个文档表示成一个“词袋（Bag-of-Words）+ 权重”的形式：

$${\mathbf{s}}_d=\{(t_i,w_i)\mid w_i>\theta \}$$

• 只保留权重 $w_i$ 大于阈值的词项，形成稀疏表示
• 每篇文档就变成了一个稀疏向量，记录“出现了哪些词 + 每个词多重要”

例如：

文档d: "人工智能 正在 改变 世界"
→ 稀疏表示：
{"人工智能": 2.5, "改变": 1.8, "世界": 1.0}

第四步：构建倒排索引（Inverted Index）

我们将所有文档的稀疏向量合并，构建倒排索引：

词项	文档ID	权重
人工智能	d1	2.5
改变	d1	1.8
世界	d1	1.0
AI	d2	2.2

倒排索引支持快速查找“哪些文档出现了这个词”。

第五步：查询时相同流程生成 query 向量 → 共现打分

假设用户发起一个查询：

query: "人工智能 改变 生活"

通过编码器和投影头，我们也生成：

sq={"人工智能":2.0,"改变":1.5,"生活":1.2} \mathbf{s}_q = \{ "人工智能": 2.0, "改变": 1.5, "生活": 1.2 \} sq​={"人工智能":2.0,"改变":1.5,"生活":1.2}

我们就拿 query 的每个词去查倒排表，看在哪些文档中也出现，然后做打分：

打分公式（共现词 × 权重乘积）

对于某个文档 $d$，与 query 的稀疏向量 ${\mathbf{s}}_q$ 的匹配分数为：

$$\text{score}(q,d)=\sum _{t\in q\cap d}{w}_q(t)\cdot w_d(t)$$

也就是：

• 找 query 和文档中出现了相同的词 $t$
• 对每个共现词 $t$，乘两个词权重
• 所有结果加总，作为该文档对这个 query 的相关性分数

举例：

文档稀疏向量：

{"人工智能": 2.5, "改变": 1.8, "世界": 1.0}

Query 向量：

{"人工智能": 2.0, "改变": 1.5, "生活": 1.2}

共同词：

• 人工智能：2.5 × 2.0 = 5.0
• 改变：1.8 × 1.5 = 2.7

总得分：

$$\text{score}=5.0+2.7=7.7$$

---

二、密集检索器（Dense Retriever）

✅ 基本原理

密集检索器将查询和文档编码为 低维稠密向量，通常使用 神经网络（Transformer 编码器） 如：

• BERT
• RoBERTa
• Sentence-BERT（SBERT）
• DPR（Dense Passage Retriever）

其核心机制是：

• 将 query 和 passage 编码为向量 q, d
• 使用向量相似度（如余弦相似度、点积）进行相似度检索

✅ 特点

特性	说明
表达方式	语义向量（dense embedding）
索引方式	FAISS、ScaNN、Milvus
检索速度	稍慢但可加速（ANN 索引）
训练需求	通常需要监督或对比学习训练
表达能力	强语义理解，可处理同义词和语义变体

✅ 常用模型

• DPR（Facebook）
• BGE（BAAI）
• Contriever（Meta）
• GTE、mGTE、ColBERT 等

---

多向量检索（Multi-vector Retrieval）

✅ 简介：

• 不是把整个句子编码成一个向量，而是保留每个词的向量
• 查询的每个词，可以独立去“查找”文档里最相关的词

🧠 技术细节：

• Query 编码得到：

  $$H_q=[h_q^1,h_q^2,...,h_q^N]$$

• Document 编码得到：

  $$H_d=[h_d^1,h_d^2,...,h_d^M]$$

• 所有 token 两两点积：

  $$S_{i,j}=h_q^i\cdot h_d^j$$

• 池化得到最终分数：

  $$s_{\text{multi}}=\text{mean-pooling or max-pooling}(S)$$

✅ 优点：

• 支持更细粒度匹配、复杂问题建模
• 在长文档/多实体/多关键词场景中表现更好

❌ 缺点：

• 算力开销大（比 dense 慢很多）
• 多向量表示→检索加速更难，需要特殊结构（如 ColBERT、聚类压缩等）

---

✅ 三种方式总结类比表：

维度	密集检索	稀疏检索	多向量检索
输入表示	单向量 [CLS]	每词一个 scalar 权重	每词一个 token 向量
匹配方式	句子整体匹配	关键词重合匹配	token-token 对齐匹配
精度	中	高（关键词匹配准）	高（语义细粒度）
速度	快	中	慢
可解释性	中	高	中
检索效果	好（适合语义召回）	好（适合专业问答）	很好（适合复杂文本匹配）

---

有了基础的铺垫我们来了解一下Embedding 模型和ReRank 模型区别

1. Embedding 模型和ReRank 模型区别

模型类型	Embedding 模型（双塔模型）	ReRank 模型（交叉编码器）
核心任务	将文本编码为向量，计算相似度	精排，对候选文本进行语义重排序
输入方式	Query 和 Document 分别编码	Query 和 Document 一起输入
输出	向量 → 相似度打分（如余弦、点积）	单个相关性得分（如 0~1，回归或分类）
示例模型	BGE, GTE, E5, MiniLM, mBERT（BiEncoder）	BGE-Reranker, GTR-Rerank, monoT5, Jina-Reranker（CrossEncoder）

架构与工作原理

🔹 Embedding 模型（双塔 / Bi-Encoder）

Query → Encoder → 向量Q
Doc   → Encoder → 向量D
相似度(Q, D) = dot(Q, D) or cos(Q, D)

• 向量可离线计算（适合大规模索引）
• 查询时用 FAISS、Milvus、ScaNN 等做 ANN 检索

🔹 ReRank 模型（交叉编码器 / Cross-Encoder）

[CLS] Query [SEP] Doc [SEP] → Encoder → [CLS]打分

• 对每个 query-doc pair 联合建模
• 得分通常用 [CLS] token 表示
• 不可离线，在线逐对重打分（慢）

对比总结表

对比维度	Embedding 模型（BiEncoder）	ReRank 模型（CrossEncoder）
编码方式	Query 和 Doc 分开编码	Query 和 Doc 一起编码
相似度计算	向量相似度（点积、cosine）	直接输出得分（回归/分类）
可否离线	✅ 文档可离线向量化	❌ 只能在线处理
检索速度	非常快，适合大规模库	慢，不能直接检索
准确性	粗排（Recall 好）	精排（Precision 好）
应用场景	初始检索、ANN、语义匹配任务	rerank、问答对齐、排序优化
模型体积	小（几十 M ~ 数百 M）	大（通常是 Transformer 全模型）
代表模型	BGE-small, GTE-base, E5-base	BGE-Reranker, monoT5, Jina-Reranker

举个例子理解

假设你要问：

“中国最长的河流是什么？”

• Embedding 阶段找到可能相关文档：

  • Doc1: “黄河是中华文明的摇篮”
  • Doc2: “长江是中国最长的河流”
  • Doc3: “珠江是中国南方主要水系”

→ 因为 "黄河" 和 "中华文明" 在向量空间里可能也靠近，所以 Doc1 也被粗排进来。

• ReRank 阶段会判断：

  • Doc1 与 query 的实际语义匹配度低
  • Doc2 精确回答了 query，得分最高
  • Doc3 得分居中

→ 最终输出顺序为：[Doc2, Doc3, Doc1]

2. rerank原理

为了衡量检索系统的有效性，主要依赖两个指标:、

• 命中率（Hit rate）：计算在前k个检索文档中找到正确答案的查询比例。简单来说，它是关于我们的系统在前几次猜测中正确的频率。
• 平均倒数排名（MRR）：对于每个查询，MRR通过查看排名最高的相关文档的排名来评估系统的准确性。具体来说，它是所有查询中这些秩的倒数的平均值。因此，如果第一个相关文档是顶部结果，则倒数排名为1;如果是第二个，倒数是1/2，以此类推。

Rerank技术分类

非监督类型

我们可以通过prompt工程来提升rerank效果，不依赖标注数据，而是直接利用LLM的语言能力来评估查询与文档的相关性，通过prompt引导模型生成相关性评分。这种方法可以分为三种： pointwise, listwise, pairwise。

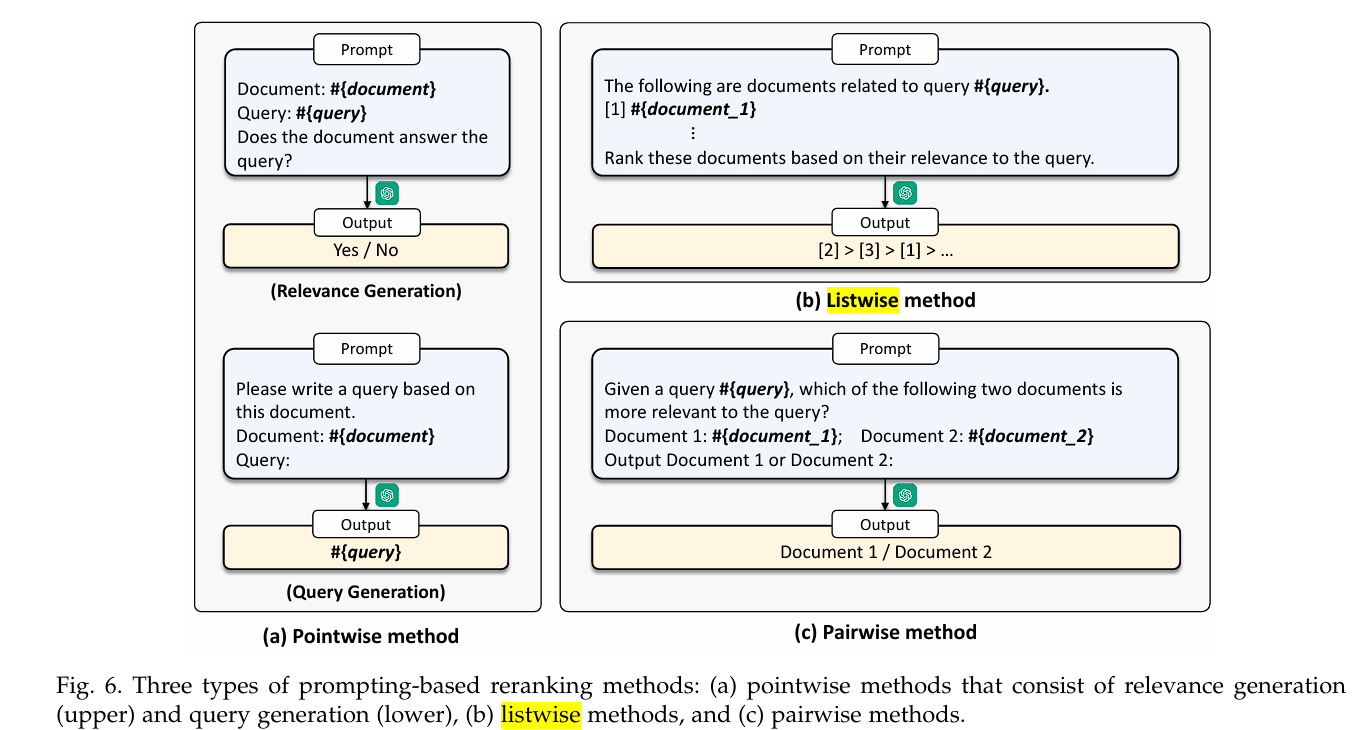
Point-wise方法

原理：Point-wise方法将重排序问题转化为回归或分类问题，独立地对每个查询-文档对进行相关性评分。

特点：

• 简单直观，易于实现
• 对每个文档独立评分，不考虑文档间的相对关系
• 适用于大规模数据处理

常见实现：

• 基于TF-IDF的相关性评分
• 基于BM25的统计模型
• 简单的神经网络回归模型

示例流程：

查询: "如何优化数据库性能"
文档1: "数据库索引优化技巧" → 评分: 0.8
文档2: "Python编程基础" → 评分: 0.2
文档3: "SQL查询优化方法" → 评分: 0.9

Pair-wise方法

原理：Pair-wise方法通过比较文档对的相对相关性来进行排序，学习文档间的相对排序关系。

特点：

• 考虑文档间的相对关系
• 更符合排序任务的本质
• 训练数据需要构造文档对

基于pairwise ranking prompting (PRP)，有三种不同的变体，以优化文档排序和 rerank 过程：

1. PRP-Allpair：该方法对所有候选文档两两进行比较，计算它们之间的优先级关系。优点是理论上能够实现最精细的排序，但其缺点也十分明显——时间复杂度为 $O(N^2)$，当候选文档数量 $N$ 较大时，计算成本极高，导致效率严重下降，不适合大规模实时场景。

2. PRP-Sorting：该方法借助高效的排序算法（如快速排序或堆排序），通过对文档集合进行整体排序来间接实现排序目标。相较于 Allpair 方法，时间复杂度降低至 $O(N\log N)$，显著提升了排序效率。该方法适用于对所有文档都需要排序的中等规模场景，平衡了准确性和计算开销。

3. PRP-Sliding-K：该方法专注于关注前 $K$ 个最相关文档的排序，采用类似冒泡排序的思想，利用滑动窗口对文档进行局部比较和调整。由于 rerank 任务通常只关心 top-$K$ 文档，且 $K$ 相对较小，因此总体时间复杂度为 $O(K\log N)$，在保证排序质量的同时，大幅降低了计算复杂度，特别适合实时性要求较高且只需输出少量高相关文档的应用场景。

List-wise方法

原理：List-wise方法直接对整个文档列表进行优化，学习最优的排序顺序。

特点：

• 直接优化整体排序质量
• 计算复杂度较高
• 更符合实际应用场景

---

监督类型

BERT类模型

原理：基于BERT等预训练语言模型，通过fine-tuning学习查询-文档的相关性。

架构特点：

• 使用[CLS]token的输出作为相关性特征
• 支持端到端训练
• 能够捕捉深层语义信息

训练过程：

输入: [CLS] 查询 [SEP] 文档 [SEP]
输出: 相关性分数 (0-1)

Cross-Encoder模型

原理：将查询和文档拼接作为输入，通过transformer模型学习两者的交互关系。

优势：

• 能够充分建模查询-文档间的交互
• 性能通常优于双塔模型
• 适合精排任务

劣势：

• 推理速度较慢
• 不适合大规模实时检索

Bi-Encoder模型

原理：使用两个独立的encoder分别编码查询和文档，通过相似度计算进行排序。

优势：

• 推理速度快
• 支持预计算文档embedding
• 适合大规模部署

劣势：

• 交互能力有限
• 性能通常低于Cross-Encoder

---

BGE-M3模型详解

bge-reranker

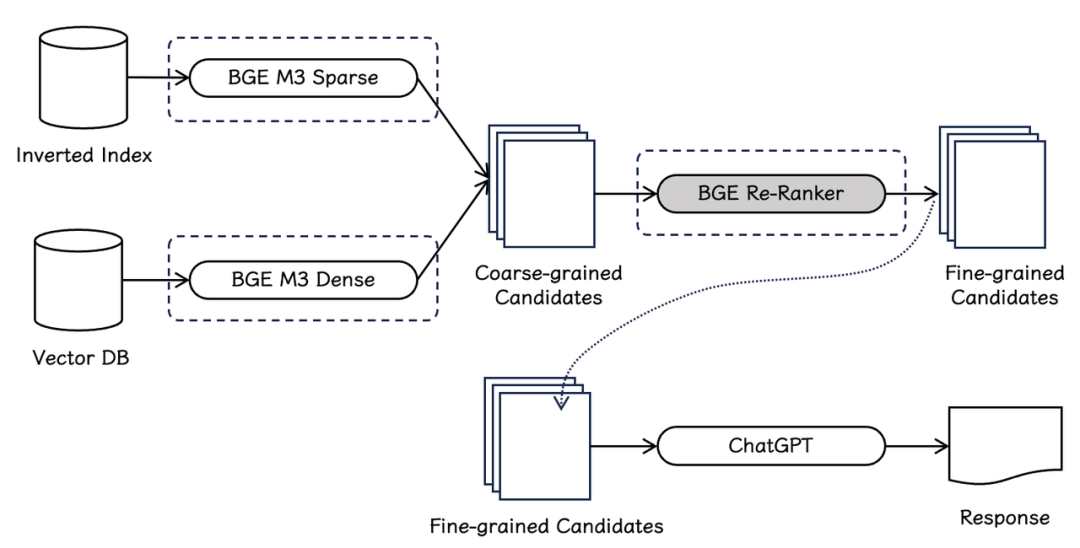
使用代码：

from FlagEmbedding import BGEM3FlagModel# 初始化模型
model = BGEM3FlagModel('BAAI/bge-m3', use_fp16=True)# 准备数据
query = "如何优化机器学习模型性能"
documents = ["机器学习模型调优技巧和方法","深度学习网络优化策略","Python编程基础教程"
]# 重排序
rerank_scores = model.compute_score(sentence_pairs=[(query, doc) for doc in documents],batch_size=32,max_length=512
)# 排序结果
sorted_docs = sorted(zip(documents, rerank_scores), key=lambda x: x[1], reverse=True)

模型概述

BGE-M3（BAAI General Embedding Model 3）是智源研究院开发的多语言、多功能、多粒度的embedding模型，特别适用于RAG系统的rerank任务。

核心特性

多语言支持（Multi-Lingual）

• 支持超过100种语言
• 在中英文等主要语言上表现优异
• 跨语言检索和重排序能力强

多功能性（Multi-Functionality）

• Dense Retrieval：支持密集向量检索
• Sparse Retrieval：支持稀疏向量检索（类似BM25）
• Multi-Vector：支持多向量表示
• Reranking：专门优化的重排序功能

原理

BGE-M3 是一个支持多种检索方式的 embedding 模型，它同时支持：我们最开始说的三种检索方式。

并使用自蒸馏的技术：

之前说的三种方法都会产生一个分数 s₁, s₂, s₃：

1. 把这三个分数加权平均 → 作为“老师分数” $s^T$
2. 再用 softmax 转成概率（越相关的打分越高）
3. 把这个老师信号当目标，让每一种方法都去拟合老师分布

这就是“自蒸馏”：模型用自己的多个子结果互相指导学习，就像自己教自己怎么融合知识。

训练流程

1. 输入数据准备

• 输入：
  一个查询（Query） $q$
  多个候选文档（Document）集合 D={d1,d2,…,dN}D = \{d_1, d_2, \ldots, d_N\}D={d1​,d2​,…,dN​}
  其中 $d^{+}$ 是与 $q$ 相关的正样本，其他为负样本

2. 编码器产生Embedding

• 对 Query 和 Documents 分别用 BGE-M3编码器：
  输出查询的隐层向量序列 $H_q=[h_q^1,h_q^2,...,h_q^N]$
  输出文档的隐层向量序列 $H_d=[h_d^1,h_d^2,...,h_d^M]$

3. 计算三种相似度分数

（1）密集检索分数 $s_{\text{dense}}$

• 取 $[CLS]$ token对应向量（$H_q[0],H_d[0]$）

• 归一化后计算内积：

  $$s_{\text{dense}}={\hat{H}}_q[0]\cdot {\hat{H}}_d[0]$$

（2）稀疏检索分数 $s_{\text{sparse}}$

• 计算每个 token 的权重（通过线性层等）

• 对 query 和文档的共现词，取最大词权重累加求和：

  $$s_{\text{sparse}}=\sum _{w\in q\cap d}\max \text{weight}(w)$$

（3）多向量检索分数 $s_{\text{multi}}$

• 计算 query 和文档所有token两两向量点积

• 通过池化（max 或 mean）汇总成分数：

  smulti=pooling({Hq[i]⋅Hd[j]}) s_{\text{multi}} = \text{pooling}(\{H_q[i] \cdot H_d[j]\}) smulti​=pooling({Hq​[i]⋅Hd​[j]})

4. 计算 InfoNCE 损失 $\mathcal{L}$

• 对每种相似度分数，分别计算 InfoNCE 对比损失，目标是区分正负样本：

$${\mathcal{L}}_{\text{dense}}=\text{InfoNCE}(s_{\text{dense}}),{\mathcal{L}}_{\text{sparse}}=\text{InfoNCE}(s_{\text{sparse}}),{\mathcal{L}}_{\text{multi}}=\text{InfoNCE}(s_{\text{multi}})$$

• 总 InfoNCE 损失：

$$\mathcal{L}={\mathcal{L}}_{\text{dense}}+{\mathcal{L}}_{\text{sparse}}+{\mathcal{L}}_{\text{multi}}$$

5. 计算自蒸馏损失 ${\mathcal{L}}^{\prime }$

• 先融合三种相似度分数生成“教师分数” $s^T$：

  $$s^T={\lambda }_1{s}_{\text{dense}}+{\lambda }_2{s}_{\text{sparse}}+{\lambda }_3{s}_{\text{multi}}$$

• 对每种分数，计算它们和教师分数的 KL 散度蒸馏损失：

  $${\mathcal{L}}_{\text{dense}}^{\prime }=\text{KL}(\text{softmax}(s^T)\parallel \text{softmax}(s_{\text{dense}}))$$

  同理计算 ${\mathcal{L}}_{\text{sparse}}^{\prime }$ 和 ${\mathcal{L}}_{\text{multi}}^{\prime }$

• 总蒸馏损失：

$${\mathcal{L}}^{\prime }={\mathcal{L}}_{\text{dense}}^{\prime }+{\mathcal{L}}_{\text{sparse}}^{\prime }+{\mathcal{L}}_{\text{multi}}^{\prime }$$

6. 最终总损失函数

$$\boxed{{\mathcal{L}}_{final}=\frac{\mathcal{L}+{\mathcal{L}}^{\prime }}{2}}$$

用于模型反向传播和参数更新。