SHAP分析+贝叶斯优化BP神经网络+新数据预测+K折交叉验证+相关性分析+孤立森林异常值处理，Matlab代码实现，作者：机器学习之心！

SHAP分析+贝叶斯优化BP神经网络+新数据预测+K折交叉验证+相关性分析+孤立森林异常值处理，Matlab代码实现，作者：机器学习之心！

效果一览

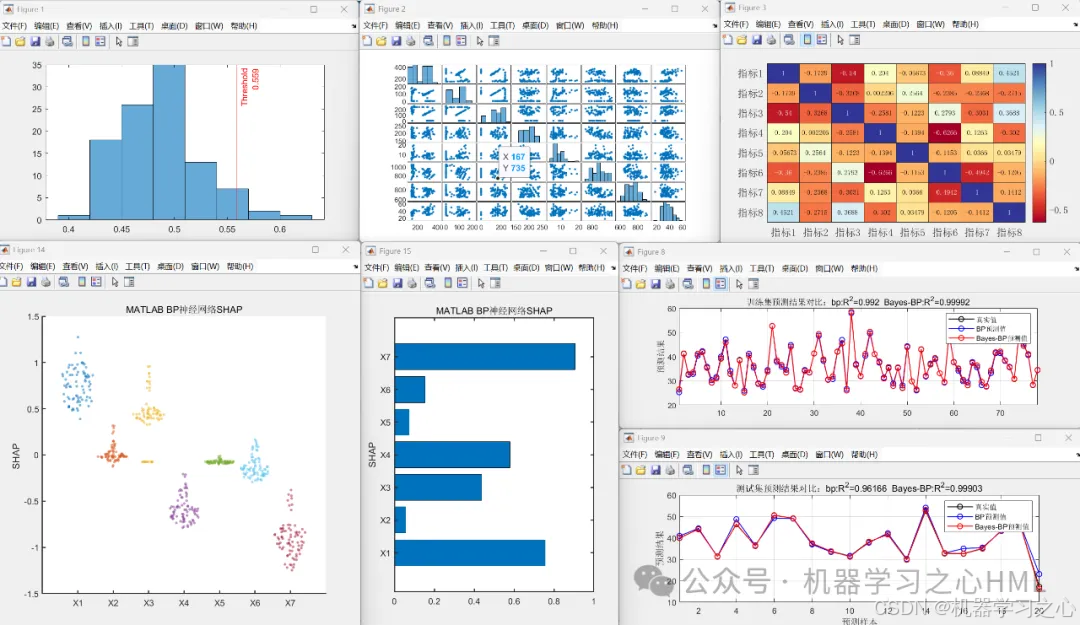
基本介绍

该代码实现了一个完整的BP神经网络回归预测分析流程，主要功能包括：

数据预处理：处理缺失值（样条插值）、检测并剔除异常值（箱线图 + 孤立森林）。

特征分析：变量相关性分析（热力图）。

模型构建与优化：构建BP神经网络（ReLU激活），通过交叉验证和贝叶斯优化调整超参数。

模型评估：计算R²、MAE、MBE、MAPE、RMSE等指标，对比调优前后模型性能。

可解释性分析：SHAP值分析特征重要性。

预测应用：对新数据（待预测.xlsx）进行预测并保存结果。

算法步骤
数据导入与清洗：

读取Excel数据，转换为数值数组。

识别缺失值，使用样条插值填补缺失列。

通过箱线图和孤立森林检测异常值，剔除异常样本。

数据划分与归一化：

按8:2划分训练集和测试集，随机打乱数据。

使用mapminmax归一化数据。

模型训练与调优：

初始模型：双隐藏层（8-8神经元），ReLU激活函数。

交叉验证：5折交叉验证评估模型稳定性。

超参数优化：贝叶斯优化自动调整参数（如正则化系数等）。

评估与可视化：

对比调优前后模型的损失曲线、预测结果散点图。

计算R²、MAE等指标，分析训练集和测试集表现。

模型解释与预测：

SHAP分析特征重要性，生成蜂群图和条形图。

加载新数据，预测结果并保存至Excel。

算法原理
缺失值处理：样条插值法通过分段多项式插值填补缺失值，保持数据平滑性。

异常检测：

箱线图基于四分位数（IQR）识别离群点。

孤立森林通过随机分割数据空间隔离异常点（高隔离效率）。

回归神经网络：全连接网络，ReLU激活函数引入非线性，损失函数为均方误差（MSE）。

贝叶斯优化：基于高斯过程建模超参数空间，最大化采集函数（EI+）寻找最优参数组合。

SHAP分析：基于博弈论分配特征贡献值，量化各特征对预测结果的影响。

参数设置
数据预处理：

插值方法：样条插值（spline）。

孤立森林污染分数：0.05（剔除5%异常值）。

模型训练：

初始网络结构：[8 8]隐藏层，激活函数为ReLU。

正则化系数：λ=0.005（防止过拟合）。

交叉验证：5折交叉验证。

超参数优化：最大评估次数10次，采集函数为expected-improvement-plus。

数据划分：训练集占比80%。

应用场景
结构化数据预测：适用于房价预测、销量预测、能源需求预测等回归问题。

高噪声数据场景：能有效处理缺失值和异常值（如传感器数据、金融数据）。

可解释性要求高的场景：SHAP分析帮助理解特征贡献。

自动化模型调优：贝叶斯优化减少人工调参成本，适合快速迭代的工业应用。

数据集

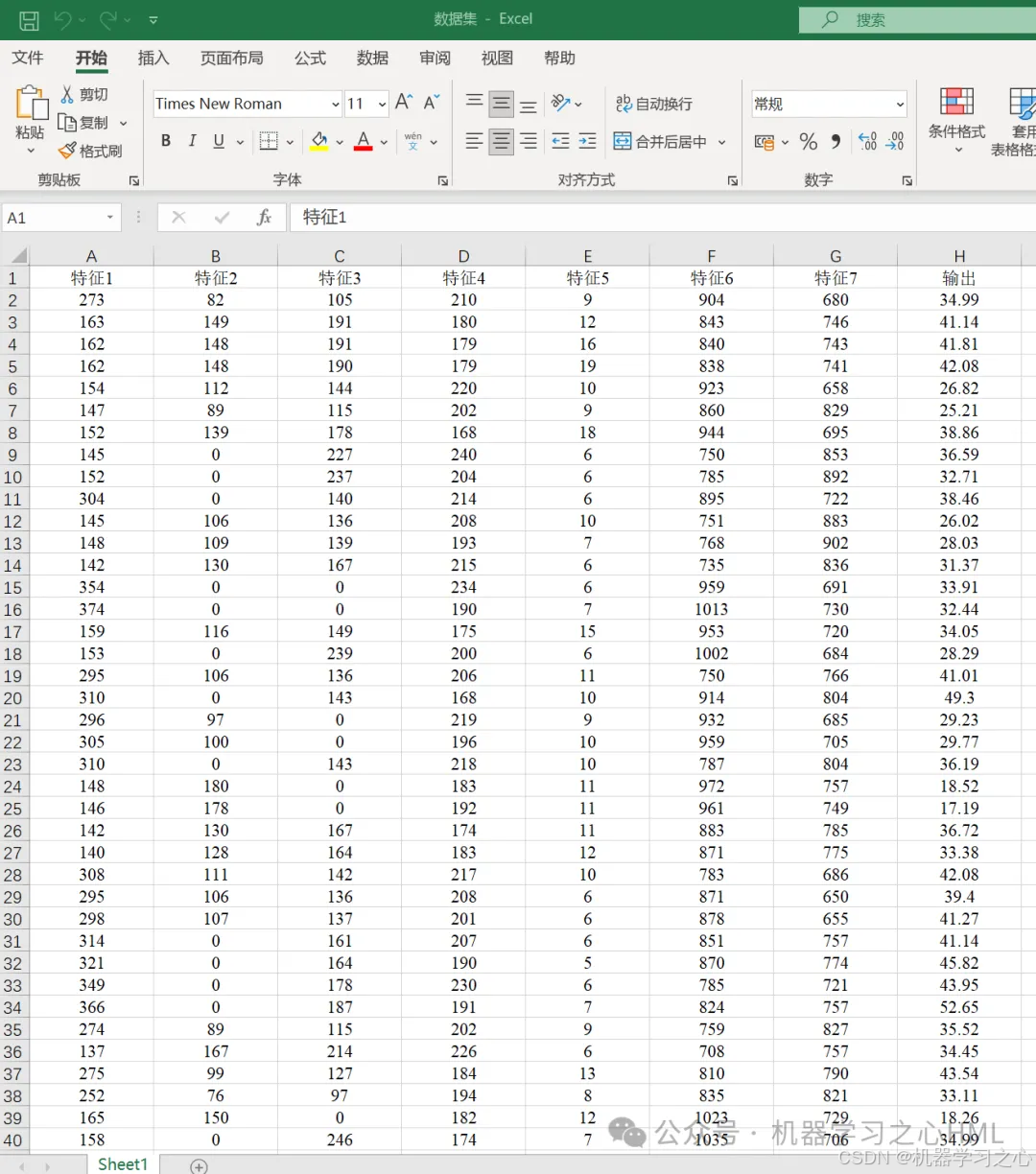
程序设计

• 完整程序和数据下载私信博主回复SHAP分析+贝叶斯优化BP神经网络+新数据预测+K折交叉验证+相关性分析+孤立森林异常值处理，Matlab代码实现，作者：机器学习之心！。

.rtcContent { padding: 30px; } .lineNode {font-size: 10pt; font-family: Menlo, Monaco, Consolas, "Courier New", monospace; font-style: normal; font-weight: normal; }
%% 划分训练集和测试集前准备
num_size = 0.8;                              % 训练集占数据集比例
outdim = 1;                                  % 最后一列为输出
num_samples = size(res, 1);                  % 样本个数
res = res(randperm(num_samples), :);         % 打乱数据集（不希望打乱时，注释该行）
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度
%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0.0001, 1);
p_test = mapminmax('apply', P_test, ps_input);
p_train = p_train';
p_test = p_test';
[t_train, ps_output] = mapminmax(T_train, 0.0001, 1);
t_test = mapminmax('apply', T_test, ps_output);
t_train = t_train';
t_test = t_test';
%% 模型训练
% fitrnet()是一个将回归神经网络模型拟合到训练数据的函数
figure 
iteration = Mdl.TrainingHistory.Iteration;
trainLosses = Mdl.TrainingHistory.TrainingLoss;
plot(iteration,trainLosses,'LineWidth',1.5)
% legend(["Training","Validation"])
xlabel("Iteration")
ylabel("Mean Squared Error")
figure 
iteration = Mdl2.TrainingHistory.Iteration;
trainLosses = Mdl2.TrainingHistory.TrainingLoss;
plot(iteration,trainLosses,'LineWidth',1.5)
% legend(["Training","Validation"])
xlabel("Iteration")
ylabel("Mean Squared Error")

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/128163536?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128151206?spm=1001.2014.3001.5502