51单片机编程学习笔记——无源蜂鸣器演奏《祝你生日快乐》
大纲
- 蜂鸣器分类
- 有源蜂鸣器
- 无源蜂鸣器
- 电路图
- 发声
- 演奏《祝你生日快乐》
- 模拟88键钢琴发声
- 音符时值(Note Value)
- 演奏
- 完整代码
蜂鸣器是一种常用的电子发声器件,有源蜂鸣器和无源蜂鸣器在工作原理和特性上有明显区别。
蜂鸣器分类
有源蜂鸣器
- 工作原理
内部自带振荡电路,接通直流电源后,振荡电路能产生固定频率的信号,从而驱动蜂鸣片发声。这里的 “有源” 指的是它自身含有电源(振荡电路所需的能源)。 - 特点
- 发声较为简单,只需接入合适的直流电压即可发声,无需外部提供驱动信号,使用方便。
- 通常有特定的发声频率,声音较为单一、稳定。
- 工作电压一般较低,常见的有 3V、5V 等。
- 应用场景
常用于各种电子设备的状态提示,如电脑、打印机、报警器等,当设备出现故障、完成操作或需要提醒用户时,有源蜂鸣器会发出特定的声音。
无源蜂鸣器
- 工作原理
内部没有振荡电路,需要外部输入一定频率的脉冲信号(如方波信号)才能发声。“无源” 意味着它自身不含振荡源,需要依赖外部的信号源来驱动。 - 特点:
- 需要搭配驱动电路来提供脉冲信号,使用相对复杂一些,但灵活性较高。
- 通过改变输入信号的频率,可以发出不同音调的声音,能够实现更丰富的音效,如演奏简单的音乐等。
- 工作电压范围相对较宽,可根据具体的应用需求进行选择。
- 应用场景
在一些需要多样化声音效果的电子设备中较为常见,如电子玩具、智能音箱、电子琴等,通过编程控制输入信号的频率和时长,无源蜂鸣器可以发出各种不同的声音,增加设备的趣味性和交互性。
电路图
在我买的电路板上的蜂鸣器是无源蜂鸣器,它的引脚信息如下图
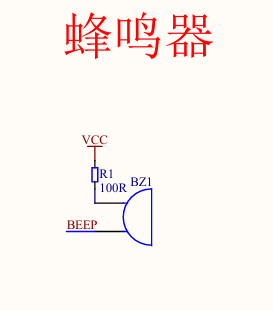
可以看到它有一个Beep引脚,该引脚给无源蜂鸣器提供了脉冲信号。
该引脚又会连接到ULN2003D达林顿阵列的12号引脚上。

我们再看下达林顿阵列的电路图

达林顿阵列(Darlington Array)是一种集成化的功率晶体管阵列,由多个达林顿管组合而成。其核心特性使其成为驱动高功率负载(如步进电机、继电器、电磁阀等)的理想选择。
达林顿管是由两个三极管级联组成,第一级三极管的发射极连接到第二级三极管的基极,形成极高的电流增益(β 值可达数千)。这样我们只需极小的基极电流即可驱动大负载电流,适合与微控制器(如 Arduino、单片机)直接连接。
达林顿管的工作原理是:当输入引脚为高电平时,对应的内部达林顿管导通。导通后,会将输出引脚拉低至接近地电位,即输出低电平。所以我们将其看做一个逻辑非的电路。
发声
无源蜂鸣器发声是通过外部电路提供不同频率的方波信号,使蜂鸣器内部的压电陶瓷片周期性振动,从而发出不同音高的声音。所以我们只要让达林顿阵列的12号引脚输出一定频率的方波信号即可。
sbit beep = P2^5; // Buzzer pin
beep = !beep;

演奏《祝你生日快乐》
模拟88键钢琴发声
按键的顺序,其每个键的声音频率是
键号 音名 频率 (Hz) 键号 音名 频率 (Hz) 键号 音名 频率 (Hz) 键号 音名 频率 (Hz)
---------------------------------------------------------------------------------------------------------------
1 A0 27.50 23 F#2 92.50 45 D4 293.66 67 B5 987.77
2 A#0 29.14 24 G2 97.99 46 D#4 311.13 68 C6 1046.50
3 B0 30.87 25 G#2 103.83 47 E4 329.63 69 C#6 1108.73
4 C1 32.70 26 A2 110.00 48 F4 349.23 70 D6 1174.66
5 C#1 34.65 27 A#2 116.54 49 F#4 369.99 71 D#6 1244.51
6 D1 36.71 28 B2 123.47 50 G4 392.00 72 E6 1318.51
7 D#1 38.89 29 C3 130.81 51 G#4 415.30 73 F6 1396.91
8 E1 41.20 30 C#3 138.59 52 A4 440.00 74 F#6 1479.98
9 F1 43.65 31 D3 146.83 53 A#4 466.16 75 G6 1567.98
10 F#1 46.25 32 D#3 155.56 54 B4 493.88 76 G#6 1661.22
11 G1 49.00 33 E3 164.81 55 C5 523.25 77 A6 1760.00
12 G#1 51.91 34 F3 174.61 56 C#5 554.37 78 A#6 1864.66
13 A1 55.00 35 F#3 185.00 57 D5 587.33 79 B6 1975.53
14 A#1 58.27 36 G3 196.00 58 D#5 622.25 80 C7 2093.00
15 B1 61.74 37 G#3 207.65 59 E5 659.25 81 C#7 2217.46
16 C2 65.41 38 A3 220.00 60 F5 698.46 82 D7 2349.32
17 C#2 69.30 39 A#3 233.08 61 F#5 739.99 83 D#7 2489.02
18 D2 73.42 40 B3 246.94 62 G5 783.99 84 E7 2637.02
19 D#2 77.78 41 C4 261.63 63 G#5 830.61 85 F7 2793.83
20 E2 82.41 42 C#4 277.18 64 A5 880.00 86 F#7 2959.96
21 F2 87.31 43 D4 293.66 65 A#5 932.33 87 G7 3135.96
22 F#2 92.50 44 D#4 311.13 66 B5 987.77 88 G#7 3322.44
我们不用在代码中硬编码这些频率,因为它们是有公式计算的
f = 440 × 2^((n-49)/12)
一个方波是由一个高电平和一个低电平组成的,所以我们每隔半个周期翻转一次电平
beep = !beep;
delay_us(half_period_us);

音符时值(Note Value)
在钢琴演奏中,每个琴键按下的时长在音乐理论中通常与音符时值(Note Value)相关。它指的是音符持续的时间长度,直接影响音乐的节奏和表现力。
如果我们知道音符时值,又知道每个音符的频率,则可以计算出该音符需要循环多少个周期以达到音符时值。
noteValueSeconds /(1 Second / freq)
以G#7键的频率3322.44Hz为例,每个方波的周期是1000 * 1000 / 3322.44=300.98us。
如果G#7要持续0.5s,则需要位置该频率方波0.5 * 1000 * 1000 / 300.98=1661个周期。
在代码上,我们以ms为单位,表示音符持续时长,则计算公式是
ms * 1000 / (1000 * 1000 / freq)
由于单片机算力有限,我们要尽量简化计算过程,这样可以尽量减少计算对音符持续时长和频率的影响。于是上述可以简化成
ms * freq / 1000
演奏
下面play_key方法可以模拟一个音符(freq)持续的时长(ms)。
sbit beep = P2^5; // Buzzer pinvoid delay_us(unsigned long us) {while(us--) {_nop_();_nop_();_nop_();// 粗略1us,实际可根据晶振微调}
}double calculate_frequency(int n) {// 88键钢琴编号:n=1为A0(27.5Hz),n=49为A4(440Hz)// 公式:f = 440 × 2^((n-49)/12)return 440.0 * pow(2.0, (n - 49) / 12.0);
}void play_key(double freq, unsigned int ms) {unsigned long total_cycles = (unsigned long)(freq * ms / 1000); // 周期次数unsigned long half_period_us = (unsigned int)(500.0 * 1000 / freq ); // 半周期usunsigned long i;for (i = 0; i < total_cycles; i++) {beep = !beep;delay_us(half_period_us / 100);}beep = 0;
}
需要注意的是,delay_us并没有传递half_period_us ,而是传递了half_period_us / 100。这是因为在51单片机上,每条 nop() 指令加上循环和函数调用的开销,实际延时会比1微秒长很多(可能是几十甚至上百微秒)。如果直接用 delay_us(half_period_us);,实际延时会远大于应有的半周期,导致频率大大降低,音调变得很低。除以100是为了补偿 delay_us 的“虚假”延时,让实际输出的方波频率接近正确的频率。
完整代码
#include <REG52.H>
#include <intrins.h>
#include <math.h>sbit beep = P2^5; // Buzzer pinvoid delay_us(unsigned long us) {while(us--) {_nop_();_nop_();_nop_();// 粗略1us,实际可根据晶振微调}
}double calculate_frequency(int n) {// 88键钢琴编号:n=1为A0(27.5Hz),n=49为A4(440Hz)// 公式:f = 440 × 2^((n-49)/12)return 440.0 * pow(2.0, (n - 49) / 12.0);
}void play_key(double freq, unsigned int ms) {unsigned long total_cycles = (unsigned long)(freq * ms / 1000); // 周期次数unsigned long half_period_us = (unsigned int)(500.0 * 1000 / freq ); // 半周期usunsigned long i;for (i = 0; i < total_cycles; i++) {beep = !beep;delay_us(half_period_us / 100);}beep = 0;
}// 88键钢琴编号:n=1为A0(27.5Hz),n=40为C4,n=42为D4,n=44为E4,n=45为F4,n=47为G4,n=49为A4,n=51为B4,n=52为C5
// 《祝你生日快乐》C调主旋律
static const int code melody[] = {40, 40, 42, 40, 45, 44, // C4 C4 D4 C4 F4 E440, 40, 42, 40, 47, 45, // C4 C4 D4 C4 G4 F440, 40, 52, 49, 45, 44, 42, // C4 C4 C5 A4 F4 E4 D451, 51, 49, 45, 47, 45 // B4 B4 A4 F4 G4 F4
};
static const int code length[] = {300, 300, 600, 600, 600, 1200,300, 300, 600, 600, 600, 1200,300, 300, 600, 600, 600, 600, 1200,300, 300, 600, 600, 600, 1200
};void main() {int i;int notes = sizeof(melody) / sizeof(melody[0]);while (1) {for (i = 0; i < notes; i++) {play_key(calculate_frequency(melody[i]), length[i]*5);}}
}
