集成运算放大器知识汇总

一、集成运放的组成

集成运算放大器，就是通过内部元器件的电参量关系将电参量进行运算，达到放大的目的。我们拆解来看：

• 集成：将电路封装，留出接口，使其模块化，便于移植。
• 运算：这里涉及到的是一些数学运算，不过这里的运算对象不是简单的数字，而是电参量，是对电参量进行了加减乘除、积分、微分等计算。
• 放大器：就是把电参量进行放大，比如把电压从1V放大至5V。

集成运算放大器的内部电路一般由四部分组成：

• 输入级：差动放大电路，以抑制零点漂移
• 中间级：共射放大电路，以提高电压放大倍数
• 输出级：互补对称输出级电路，以提高带负载能力
• 偏置电路：电流源电路，以提供静态偏置电流

二、集成运放的特性

运算放大器具有两个输入端和一个输出端，如下图示，其中标有“+”号的输入端为“同相输入端”，另一标有“-”号的输入端为“反相输入端”

集成运放的电压传输特性（两个区域）：

• 线性工作区：需引入负反馈，满足虚短和虚断
• 非线性工作区：需引入正反馈或开环

线性工作区的两个特性：
虚短：由于$A_{od}$ 很大，以致于很小的差模输入就会使输出趋向于饱和的非线性区，故想在线性区工作， $u_{+}$- $u_{-}$就必须要小到一定程度，近似于“短路”，即$u_{+}$ = $u_{-}$
虚断：由于集成运放的差模输入电阻很大，故流入运放输入端的电流远小于其外电路的电流，近似于“断路”，即$i_{+}$= $i_{-}$= 0

三、集成运放经典电路

1. 反向放大器

如下图示，由虚短可知，同相和反相输入端电压为0；由虚断可知，同相和反相输入端几乎没有电路注入和流出。所以R1和R2电阻相当于串联，流过的电流相同。

$\frac{V_i-V_{-}}{R_1}=\frac{V_{-}-V_{out}}{R_2}$

其中V- = V+ = 0，所以反向放大器的输入输出关系式为：

$V_{out}=-\frac{R_1}{R_2}\ast V_i$

2. 同向放大器

如下图示，由虚短可知，同相和反相输入端电压相同为$V_i$；由虚断可知，反相输入端几乎没有电路注入和流出。所以R1和R2流过的电流相同，$V_i$等于R2上的分压。

$\frac{V_{out}}{R_1+R_2}=\frac{V_i}{R_2}$

所以同向放大器的输入输出关系式为：

$V_{out}=\frac{(R_1+R_2)}{R_2}\ast V_i$

3. 反向加法器

如下图示，由虚短可知，同相和反相输入端电压为0；由虚断可知，通过R2与R1的电流之和等于通过R3的电流。

$\frac{V_1-V_{-}}{R_1}+\frac{V_2-V_{-}}{R_2}=\frac{V_{-}-V_{out}}{R_3}$

其中V- = V+ = 0，所以加法器1的输入输出关系式为：

$V_{out}=-(\frac{V_1}{R_1}+\frac{V_2}{R_2})\ast R_3$

若取R1=R2=R3，则上式变为：

$V_{out}=-(V_1+V_2)$

4. 同向加法器

如下图示，由虚短可知，同相和反相输入端电压相同；由虚断可知，通过R2与R1的电流相等，流过R4和R3的电流也相等。

$\frac{V_1-V_{+}}{R_1}=\frac{V_{+}-V_2}{R_2}$ 以及 $\frac{V_{out}-V_{-}}{R_3}=\frac{V_{-}}{R_4}$

其中V- = V+，若R1=R2，R3=R4，则由以上式子可以推导出：

$V_{out}=V_1+V_2$

5. 减法器

如下图示，由虚短可知，同相和反相输入端电压相同；由虚断可知，通过R2与R1的电流相等，流过R4和R3的电流也相等。

$\frac{V_2-V_{+}}{R_1}=\frac{V_{+}}{R_2}$ 以及 $\frac{V_{-}-V_{out}}{R_3}=\frac{V_1-V_{-}}{R_4}$

其中V- = V+，若R1=R2，R3=R4，则由以上式子可以推导出：

$V_{out}=V_2-V_1$

6. 积分电路

如下图示，由虚短可知，同相和反相输入端电压为0；由虚断可知，通过R1的电流与通过C1的电流相等。

电容上的电压：$U_c=\frac{1}{C}{\int }_{}^{}{i}_{c}dt$

电容上的电流：$i_c=C\frac{d{U}_c}{dt}$

$\frac{V_1}{R_1}=-C\frac{d{V}_{out}}{dt}$ 推导出输出电压与输入电压对时间的积分成正比：

$V_{out}=-\frac{1}{R_1{C}_1}{\int }_{}^{}{V}_{1}dt$

若$V_1$为恒定电压U，则上式变换为：

$Vout=-\frac{U\ast t}{R_1{C}_1}$

则$V_{out}$输出电压是一条从0至负电源电压按时间变化的直线。

7. 微分电路

如下图示，由虚短可知，同相和反相输入端电压为0；由虚断可知，通过R1的电流与通过C1的电流相等。

$V_{out}=-R_1{C}_1\frac{d{V}_1}{dt}$

这是一个微分电路，如果$V_1$是一个突然加入的直流电压，则输出$V_{out}$对应一个方向与$V_1$相反的脉冲。

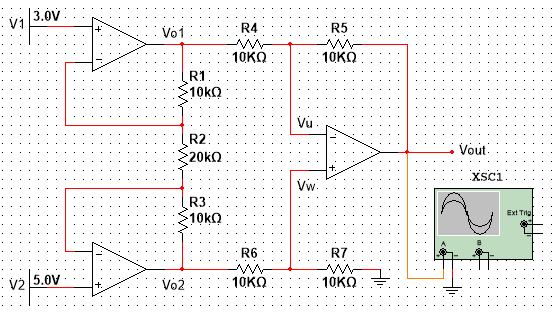
8. 差分放大电路

如下图示，由虚短可知，同相和反相输入端电压为0；由虚断可知，流过R1、R2、R3的电流相等，流过R4、R5的电流相等，流过R6、R7的电流相等。

$\frac{V_1-V_2}{R_2}=\frac{V_{O1}-V_{O2}}{R_1+R_2+R_3}$

$\frac{V_{O1}-V_u}{R_4}=\frac{V_u-V_{out}}{R_5}$ 若R4=R5，则 $V_{O1}-V_u=V_u-V_{out}$

$\frac{V_{O2}-V_w}{R_6}=\frac{V_w}{R_7}$ 若R6=R7，则$V_{O2}-V_w=V_w$

综合上面的式子，计算后得出：

$V_{out}=\frac{R_1+R_2+R_3}{R_2}\ast (V_2-V_1)$

上式中，$\frac{R_1+R_2+R_3}{R_2}$是定值，确定了差值$V_2-V_1$的放大倍数。

9. 电流检测电路

4-20mA 常用在各种检测仪表中，一般都需要通过电路将此电流转换成电压后，送入ADC转换成数字信号。下图就是一个电流检测电路，4-20mA电流流过100欧姆的采样电阻，在电阻上会产生0.4-2V的电压差。

由虚短可知，同相和反相输入端电压相等；由虚断可知，流过R2、R4的电流相等，流过R3、R5的电流相等。

$\frac{V_2-V_y}{R_3}=\frac{V_y}{R_5}$

$\frac{V_1-V_x}{R_2}=\frac{V_x-V_{out}}{R_4}$

$V_1-V_2=0.4\to 2$

若R2=R3，R4=R5，综合上面的式子，计算后得出：

$V_{out}=-\frac{R_4}{R_2}\ast (V_1-V_2)$

若R2=10K, R4=22K, 则$V_{out}=-0.88\to 4.4V$

10. 电压电流转换电路

电流可以转换成电压，当然电压也可以转换成电流。如下图示，由虚短可知，同相和反相输入端电压相等；由虚断可知，流过R2、R6的电流相等，流过R4、R5的电流相等。

$\frac{V_i-V_1}{R_2}=\frac{V_1-V_4}{R_6}$

$\frac{V_3-V_2}{R_5}=\frac{V_2}{R_4}$

若R2=R6，R4=R5，综合上面的式子，计算后得出：

$V_3-V_4=V_i$

上式说明R7两端的电压和输入电压相等，则通过R7的电流为：

$I_7=\frac{V_i}{R_7}$