当前位置：首页 > news >正文

算法（最小基因变化+迷宫中离入口最近的出口）

news 来源：原创 2025/5/20 8:24:19

题目链接：433. 最小基因变化 - 力扣（LeetCode）

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

示例 1：

输入：start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出：1

示例 2：

输入：start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出：2

示例 3：

输入：start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出：3

提示：

start.length == 8
end.length == 8
0 <= bank.length <= 10
bank[i].length == 8
start、end 和 bank[i] 仅由字符 ['A', 'C', 'G', 'T'] 组成

解法：

算法思路：

如果将「每次字符串的变换」抽象成图中的「两个顶点和⼀条边」的话，问题就变成了「边权为 1 的最短路问题」。

因此，从起始的字符串开始，来⼀次 bfs 即可

class Solution {public int minMutation(String startGene, String endGene, String[] bank) {Set<String> vis=new HashSet<>();//标记已经被搜索过的状态Set<String> hash=new HashSet<>();//标记基因库里的字符串for(String s:bank){hash.add(s);}char[] change={'A','C','G','T'};if(startGene.equals(endGene)) return 0;if(!hash.contains(endGene)) return -1;Queue<String> q=new LinkedList<>();q.add(startGene);hash.add(startGene);int step=0;while(!q.isEmpty()){step++;int sz=q.size();while(sz--!=0){String t=q.poll();for(int i=0;i<8;i++){char[] tmp=t.toCharArray();//将其转为字符数组for(int j=0;j<4;j++){tmp[i]=change[j];String next=new String(tmp);//将其友还原为字符串if(hash.contains(next)&&!vis.contains(next)){if(next.equals(endGene)) return step;q.add(next);vis.add(next);}}}}}return -1;}
}

题目链接：1926. 迷宫中离入口最近的出口 - 力扣（LeetCode）

给你一个 m x n 的迷宫矩阵 maze （下标从 0 开始），矩阵中有空格子（用 '.' 表示）和墙（用 '+' 表示）。同时给你迷宫的入口 entrance ，用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。

每一步操作，你可以往上，下，左或者右移动一个格子。你不能进入墙所在的格子，你也不能离开迷宫。你的目标是找到离 entrance 最近的出口。出口的含义是 maze 边界上的 空格子。entrance 格子不算出口。

请你返回从 entrance 到最近出口的最短路径的步数，如果不存在这样的路径，请你返回 -1 。

示例 1：

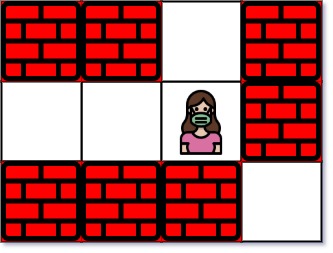
输入：maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
输出：1
解释：总共有 3 个出口，分别位于 (1,0)，(0,2) 和 (2,3) 。
一开始，你在入口格子 (1,2) 处。
- 你可以往左移动 2 步到达 (1,0) 。
- 你可以往上移动 1 步到达 (0,2) 。
从入口处没法到达 (2,3) 。
所以，最近的出口是 (0,2) ，距离为 1 步。

示例 2：

输入：maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
输出：2
解释：迷宫中只有 1 个出口，在 (1,2) 处。
(1,0) 不算出口，因为它是入口格子。
初始时，你在入口与格子 (1,0) 处。
- 你可以往右移动 2 步到达 (1,2) 处。
所以，最近的出口为 (1,2) ，距离为 2 步。

示例 3：

输入：maze = [[".","+"]], entrance = [0,0]
输出：-1
解释：这个迷宫中没有出口。

提示：

maze.length == m
maze[i].length == n
1 <= m, n <= 100
maze[i][j] 要么是 '.' ，要么是 '+' 。
entrance.length == 2
0 <= entrancerow < m
0 <= entrancecol < n
entrance 一定是空格子。

解法（bfs 求最短路）：

算法思路：

利⽤层序遍历来解决迷宫问题，是最经典的做法。

我们可以从起点开始层序遍历（利用堆），并且在遍历的过程中记录当前遍历的层数。这样就能在找到出⼝的时候，得到起点到出⼝的最短距离。

class Solution {int[] dx={0,0,-1,1};int[] dy={-1,1,0,0};int m,n;public int nearestExit(char[][] maze, int[] entrance) {m=maze.length;n=maze[0].length;boolean[][] vis=new boolean[m][n];Queue<int[]> q=new LinkedList<>();q.add(new int[]{entrance[0],entrance[1]});vis[entrance[0]][entrance[1]]=true;int step=0;while(!q.isEmpty()){step++;int sz=q.size();for(int i=0;i<sz;i++){int[] t=q.poll();int a=t[0],b=t[1];for(int j=0;j<4;j++){int x=a+dx[j],y=b+dy[j];if(x>=0&&x<m&&y>=0&&y<n&&maze[x][y]=='.'&&!vis[x][y]){//判断是否已经走出出口if(x==0||x==m-1||y==0||y==n-1){return step;}q.add(new int[]{x,y});vis[x][y]=true;}}}}return -1;}
}