Smith Chart阻抗匹配
一 阻抗匹配基础
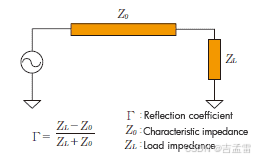
1 反射系数
┏ = (ZL -Zo) /(ZL +Zo) ,阻抗ZL 、Zo为为复数,反射系数┏ 也同样为复数,假设Zo = 50Ω ;
ZL为开路时,┏ = (+∞ - 50)/ (+∞ +50) = 1 ,在开路端产生与入射端大小相同,反向相反的反射波。
ZL= 50Ω时,┏ = (50 - 50)/ (50 +50) = 0,没有反射电压。
ZL为短路时,┏ = (0 - 50)/ (0 +50) = -1,产生负的反射波。
2 归一化阻抗
减少未知参数的数量,以特性阻抗Zo为标准归一化,ZL = R + jX,归一化后,
Z= ( R + jX) / Zo = r + jx ,r为归一化后的电阻,x为归一化后的电抗。
归一化后的反射系数 ┏ = (Z-1) / (Z+1),那么 Z = (1 + ┏) / (1 - ┏)
3 等反射系数圆
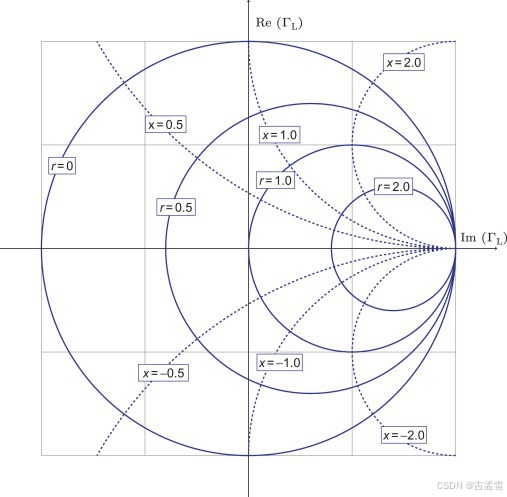
下图中┏1 = 1,┏2 = -1,┏3 = 1*i ,┏4= -1*i,由上面的反射系数分析可知,┏1=1对应ZL开路,┏2 = -1对应ZL短路,圆心位置对应ZL与Z0相同。所有落在单位圆上点的反射系数┏模相同,只有相角变化。
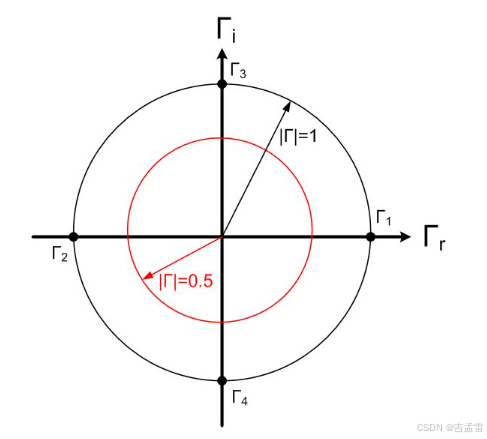
图:等反射系数圆
4 复平面上的归一化电阻圆和归一化电抗圆
由 Z =r + jx = (1 + ┏) / (1 - ┏) = (1+┏r +j┏i ) / (1-┏r -j┏i )
r + jx = {1+(┏r +j┏i ) } / {1-(┏r +j┏i )}
r + jx ={1+(┏r^2 +┏i^2 ) } / {(1-┏r)^2 +┏i ^2} + j* 2┏i / {(1-┏r)^2 +┏i ^2}
5 电阻圆(图A):
整理电阻r得到(┏r - r / r+1)^2 + ┏i^2 = (1/r+1)^2
圆心为(r / r+1 ,0),半径为1/r+1,r=1时,圆心在(0.5 ,0),半径为0.5,r=0时,圆心(0 ,0),半径为1,下图A中的黑色圆,r=0时的圆就是纯电抗圆。
6 电抗圆(图B):
整理x得到(┏r - 1)^2 + (┏I -1/x) ^2 = (1/x)^2
圆心为(1 ,1/x),半径为1/x,x=1时,圆心在(1 ,1),半径为1,x=0时,圆心(1 ,+∞),半径为+∞,下图B中横轴就是电抗为零时的纯电阻线。
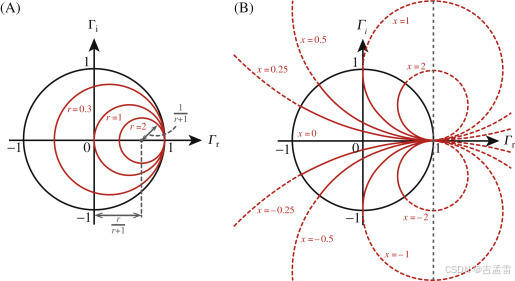
图:电阻圆与电抗圆
二 史密斯圆图
将电阻圆与电抗圆在同一个坐标系下画出就得到了完整的史密斯圆图,r=0的圆为等电抗圆,横轴为等电阻线,圆为等电阻圆,弧形为等电抗弧,横轴最左侧的点为短路点,右侧为开路点,中心为阻抗匹配点。
三 ADS的Smith Chart阻抗匹配
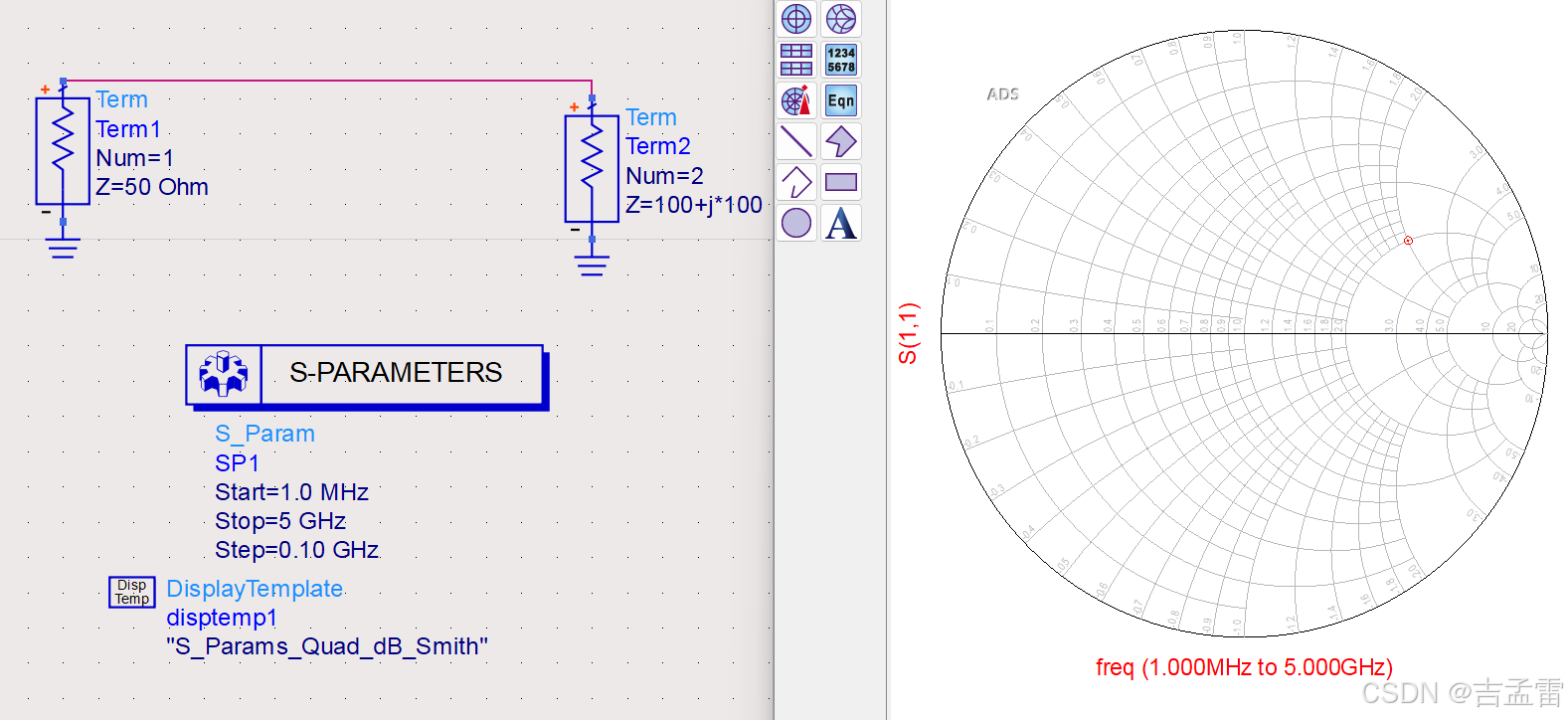
源端阻抗Zs=50Ω,负载阻抗ZL = 100+j*100,工作频率2.4G,匹配阻抗50Ω。当没有匹配网络时,在圆图上的点为r=2,x=2。
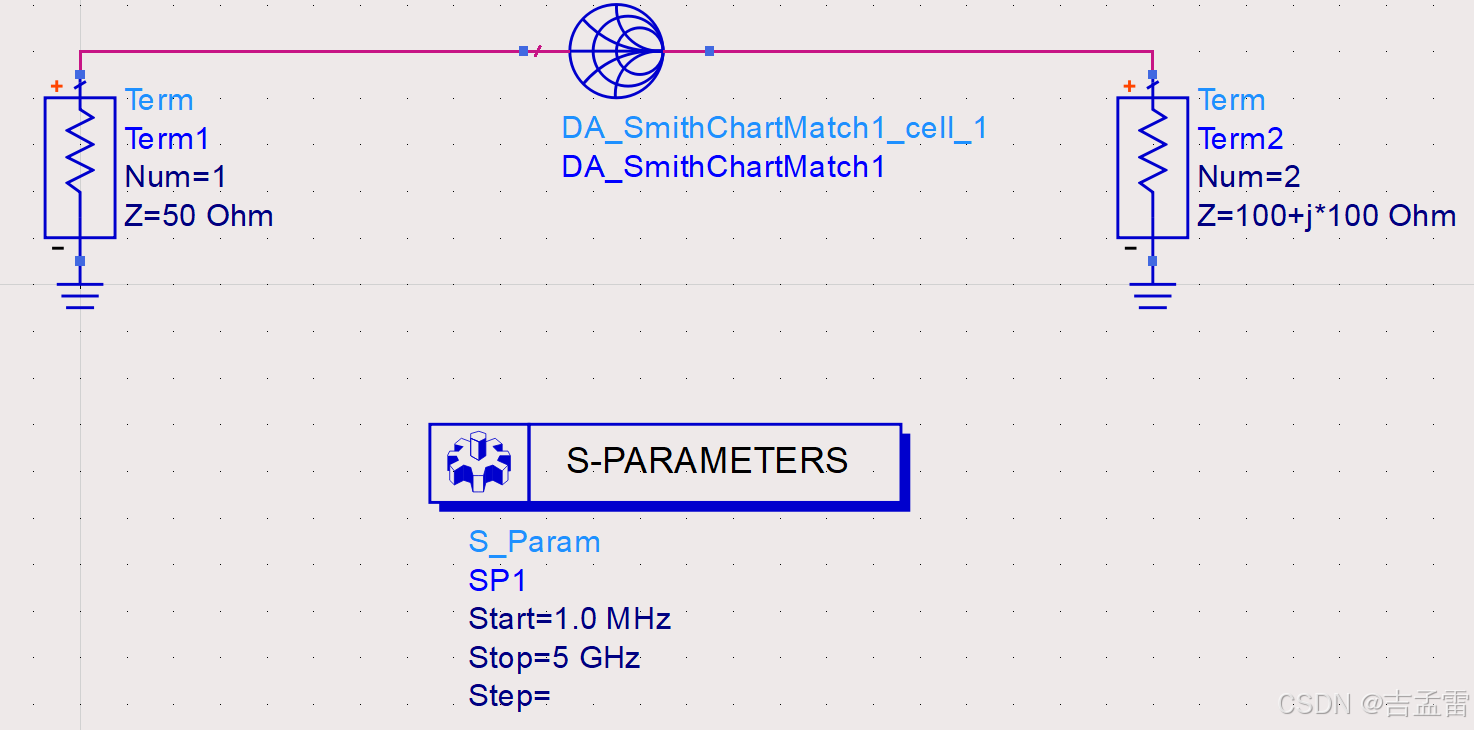
增加圆图匹配模块DA-SmithChartMatch,然后在Tools菜单下选择Smith Chart 。
选择目标频率为2.4G,源端阻抗Zs=50Ω,负载阻抗ZL = 100+j*100,选择自动生成匹配参数,可以看出经过LC网络后,阻抗匹配点变到了50Ω的位置。
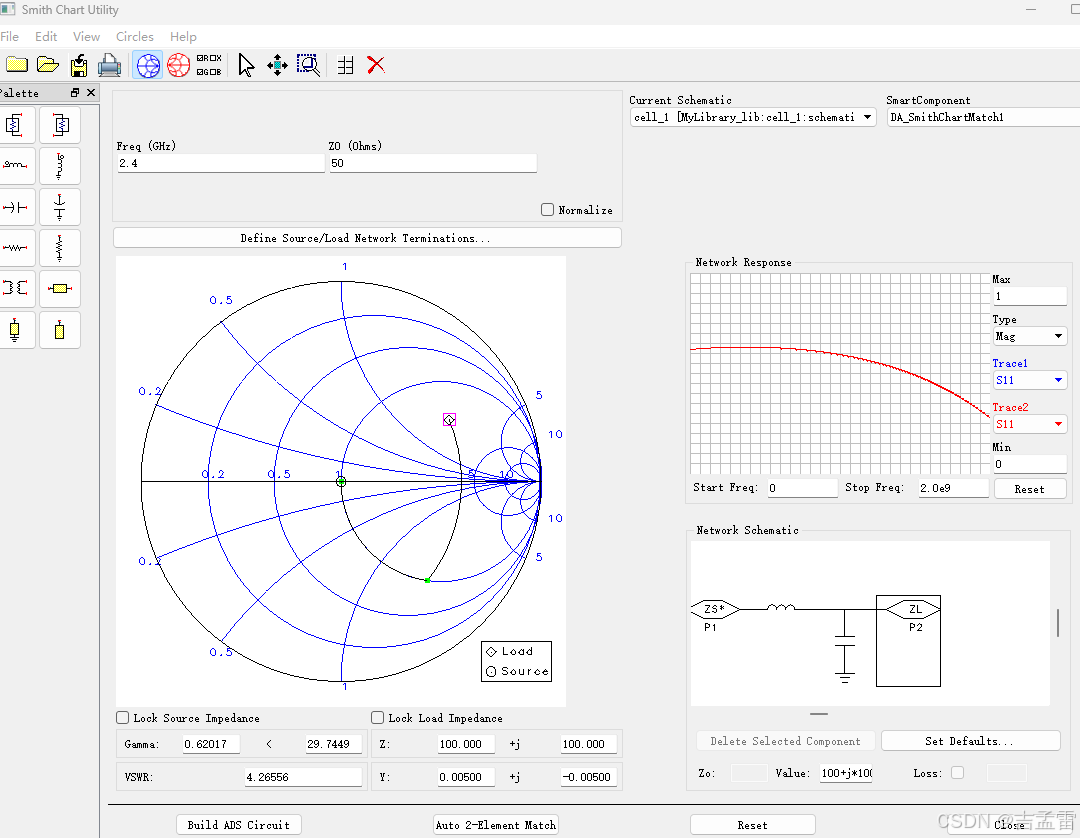
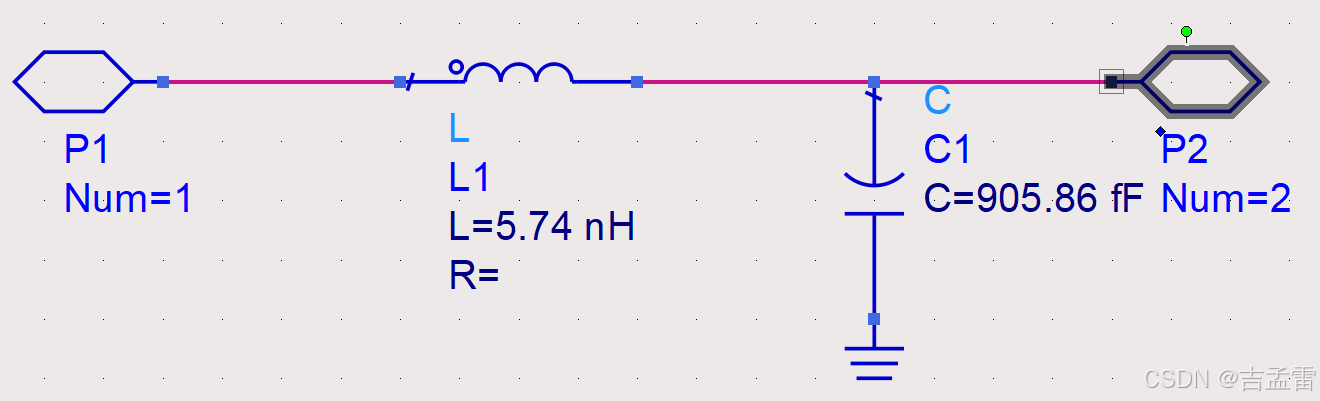
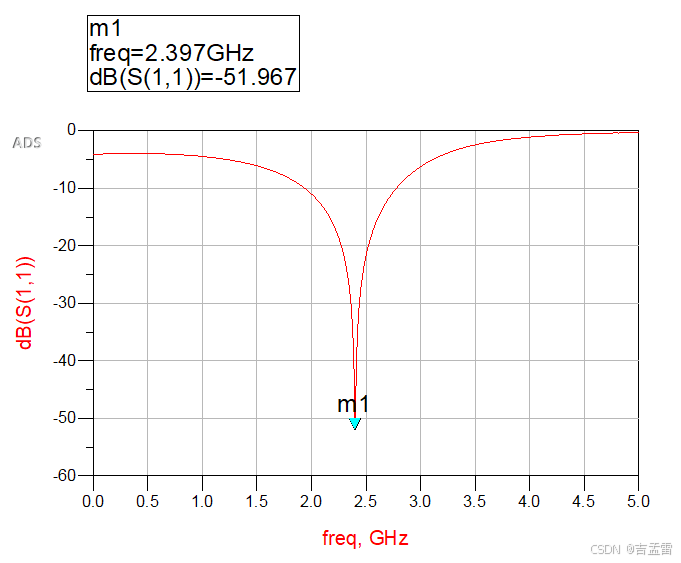
输出回波损耗S11,可以看到在2.4G位置的回波损耗很小。