当前位置： 首页 > news >正文

优选算法——双指针专题

news 来源：原创 2025/6/8 18:38:33

本章先分享关于优选算法的双指针的思路：

主要是以题目来展示常见使用双指针的思路。

ps:

双指针做法：不要被表面所迷惑，它其实是通过用一个数组的下标来充当指针

数组分两块：是⾮常常⻅的⼀种题型，主要就是根据⼀种划分⽅式，将数组的内容分成左右两部分。这种类型的题，⼀般就是使⽤「双指针」来解决
 

OJ（一）

283. 移动零 - 力扣（LeetCode）

1）题目展示

 2）解法思路：

数组分两块：一边非0，一边0，可以使用双指针法。

1.定义两个指针：

cur：从左到右扫描数据，来遍历数组

dest：已处理的区间内，非零元素的最后一个位置。

由下面我们可以看出：

分为三个区间：

[0,dest][]dest+1,cur-1][cur,n-1]

非0            0                 未处理

过程

具体做法：

1.cur遇到0，cur++

2.cur遇到非零元素：swap（dest+1，cur），cur++

代码：

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int cur=0;
    int dest=-1;
    for(cur=0;cur<nums.size();cur++)
    {
        if(nums[cur])
        {
              swap(nums[cur],nums[++dest]);
        }
        
    }
    }
};

OJ(二)

1089. 复写零 - 力扣（LeetCode）

1）题目展示：

2）解法思路：

1.双指针法：

如果「从前向后」进⾏原地复写操作的话，由于 0 的出现会复写两次，导致没有复写的数「被覆盖掉」。因此我们选择「从后往前」的复写策略。

但「从后向前」复写的时候，我们需要找到「最后⼀个复写的数」，因此我们的⼤体流程分两步：

i. 先找到最后⼀个复写的数；

ii. 然后从后向前进⾏复写操作

总结：

1.先根据“异地”操作，然后再进行双指针的“就地”操作

2.先找到最后一个复写的数：

双指针算法：

1）先判断cur的值

2）决定dest是走一步还是两步（0两步，非0一步）

3）判断dest是否已经到了结束位置

4）cur++

3.  然后从后向前进⾏复写操作。

1）i. 判断 cur 位置的值：

1. 如果是 0 ： dest 以及 dest - 1 位置修改成 0 ， dest -= 2 ；

2. 如果⾮零： dest 位置修改成 0 ， dest -= 1 ；

2）cur-- ，复写下⼀个位置
 

4.越界处理：判断 dest 是否越界到 n 的位置

eg：1 0 2 3 0 0（会越界）

如果越界，执⾏下⾯三步：

1. n - 1 位置的值修改成 0 ；

2. cur 向移动⼀步（即cur--）；

3. dest 向前移动两步（即dest-=2）
 

3）代码

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int cur=0,dest=-1;
        int n=arr.size();
        while(cur<n)
        {
           if(arr[cur]) dest++;
           else dest+=2;
           if(dest>=n-1) break;
           cur++;
        }
        if(dest==n)
        {
            arr[n-1]=0;
            cur--;
            dest-=2;
        }

        while(cur>=0)
        {
            if(arr[cur])
            {
                arr[dest--]=arr[cur--];
            }
            else
            {
                arr[dest--]=0;
                arr[dest--]=0;
                cur--;
            }
        }
    }
};

OJ快乐数（三）

202. 快乐数 - 力扣（LeetCode）

1）题目展示

2）解法思路

分析题目意思：

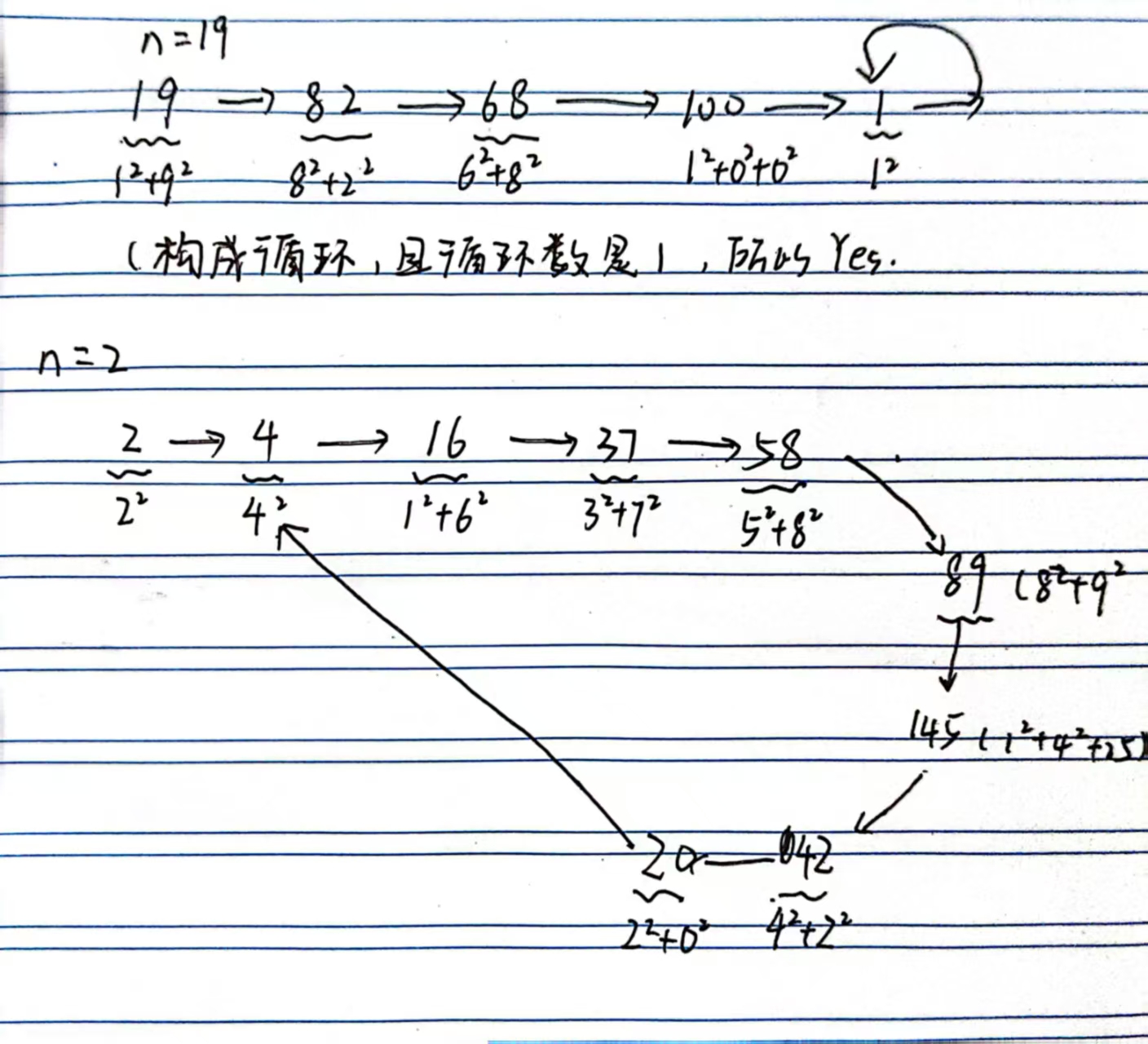
 看到这里，就与我们之前在数据结构里面OJ题写过的判断链表是否有环那题非常相似的。

那里，我们使用的是快慢指针的方法，实质也是双指针。

十道OJ题帮你深入认识链表-CSDN博客

所以，思路：

双指针的快慢指针：

1）慢指针每次向后移动一位

2.快指针每次向后移动两位

3.判断相遇时的值是否为1即可。

ps：其实这里不可能不成环的。（证明：鸽巢原理：n个巢，n+1个鸽，必有一个巢会有2只鸽子及以上）

3）代码

class Solution {
public:

    int GetNum(int n)
    {
         int num=0;
            while(n)
        {
              int ret=n%10;
              num+=ret*ret;
              n/=10;      
        }
        return num;
    }
    bool isHappy(int n) {

        int slow=n,fast=GetNum(n);

        while(slow!=fast)
        {
            slow=GetNum(slow);
            fast=GetNum(GetNum(fast));
        
        }
        return fast==1;    
    }
};

OJ（四）

11. 盛最多水的容器 - 力扣（LeetCode）

1）题目展示

2）解法思路

解法1：暴力枚举（超时）即一个一个遍历去找

解法二：利用单调性，来进行使用双指针法解决

设两指针 left , right ，分别指向⽔槽板的最左端以及最右端，此时容器的宽度为 right - left 。由于容器的⾼度由两板中的短板决定，因此可得容积公式 ： v = (j - i) * min(height[left], height[right])

为了下面的写法更加简洁，我们取高为h，宽为w，即V=h*w

下面我们就以题目的实例举例：

我们仔细观察会发现：

V=h*w，h由两板的短板决定

如果此时我们固定⼀个边界，改变另⼀个边界，⽔的容积会有如下变化形式：

--->容器的宽度⼀定变⼩。

---> 由于左边界较⼩，决定了⽔的⾼度。如果改变左边界，新的⽔⾯⾼度不确定，但是⼀定不会超

过右边的柱⼦⾼度，因此容器的容积可能会增⼤。

--->如果改变右边界，⽆论右边界移动到哪⾥，新的⽔⾯的⾼度⼀定不会超过左边界，也就是不会

超过现在的⽔⾯⾼度，但是由于容器的宽度减⼩，因此容器的容积⼀定会变⼩的。

因此：左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界，继续去判断下⼀个左右边界

总结思路：

1.定义了left和right指针后，算出体积就可以舍去小的那个值了（即left的话就++，right的话就--）

2.高取小那个。

2.接着继续算体积，每次比较那个大就保留哪个。

3）代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0,right=height.size()-1;
        int ret=0;
        while(left<right)
        {
            int v=min(height[left],height[right])*(right-left);
            ret=max(ret,v);
            //移动指针
            if(height[left]<height[right])
            {
                left++;
            }
            else
            {
                right--;
            }
        }
        return ret;
    }
};

OJ（五）

611. 有效三角形的个数 - 力扣（LeetCode）

1）题目展示

2）解法思路

数学知识：

怎么才能构成三角形？

设a<=b<=c,那么要想构成三角形，则a+b>c

解法1：暴力枚举（弄三层for循环，再检查是否构成三角形，此时的时间复杂度就为O（n^3））

解法二：

1.我们先进行数组优化（即对数组进行排序）

2.接着利用单调性，使用双指针来解决：

1） 先固定最大的数  ----->O(N)

2）在最大数的左区间内，使用双指针法，快速通过符号构成三角形的数O(N)

若如果 nums[left] + nums[right] > nums[i] ：

▪ 说明 [left, right - 1] 区间上的所有元素均可以与 nums[right] 构成⽐nums[i] ⼤的⼆元组

▪ 满⾜条件的有 right - left 种

如果 nums[left] + nums[right] <= nums[i] ：

▪ 说明 left 位置的元素是不可能与 [left + 1, right] 位置上的元素构成满⾜条件的⼆元组

▪ left 位置的元素可以舍去， left++ 进⼊下轮循环

最后，时间复杂度为O（n^2）效率提高了.

3）代码

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        int ret=0;
        for(int i=n-1;i>=2;i--)
        {
            int left=0,right=i-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>nums[i])
                {
                    ret+=right-left;
                    right--;
                }
                else
                {
                    left++;
                }
            }
        }
        return ret;
    }
};

OJ(六)

LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

1）题目展示

2）解法思路

解法一：暴力枚举

解法二：利用单调性，使用双指针来找（跟上面的很像）

因为它已经排好序了，所以我们就省去了自己是排序那一步。

定义两个指针min（指向左边），max（右边）

若price[min]+price[max]>target,利用它的单调性，我们是不是就可以直接移动max--了？你想想你连最小的数都大于target了，其他是不是更加大于？

同样的道理：price[min]+price[max]<target ，直接min++。

当price[min]+price[max]==target时，就return  {price[left],price[right]};

3）代码

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left=0,right=price.size()-1;
        int sum=0;
        while(left<right)
        {
            if(price[left]+price[right]>target)
            {
                right--;
            }
            else if(price[left]+price[right]<target)
            {
                left++;
            }
            else
            {
                return  {price[left],price[right]};
            }
        }
        return {};
    }
};

OJ（七）

15. 三数之和 - 力扣（LeetCode）

1）题目展示

2）解法思路

解法1：排序+暴力枚举+使用set（去重）

解法2：排序+双指针

1.排序

2.固定一个数a（我们从最左边第一个数先固定）

3.在固定的数的后面区间内，利用双指针，快速找到两个数的和等于-a

跟上面的题也是类似的，利用它的单调性，优化。

如果nums[left]+nums[right]>-a，即可直接right--；

nums[left]+nums[right]<-a,即可直接left++；（原因看上面的解析）

整体大概思路就完成了，

接下来我们来处理细节问题：

1.做到不漏：

解决：找到一种结果后，不要停，缩小区间，继续找

2.做到不重复

解决:

找到一种结果后，left和right都要跳过重复的数

当使用完一次双指针算法后，固定的数也要跳过重复的数。

此外，解决上面的问题的同时，还要注意避免越界的问题（代码中显示）

3）代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int i=0;
        vector<vector<int>> ret;
        while(i<nums.size())
        {
            int left=i+1,right=nums.size()-1;
            while(left<right)
            {
                if(nums[left]+nums[right]>(-nums[i]))
                {
                    right--;
                }
                else if(nums[left]+nums[right]<(-nums[i]))
                {
                    left++;
                }
                else
                {
                    ret.push_back({nums[left],nums[right],nums[i]});
                    left++;
                    right--;
                    1.防止越界
                    while(left<right && nums[left-1]==nums[left])
                    {
                        left++;
                    }
                       2.防止越界
                    while(left<right && nums[right+1]==nums[right])  
                    {
                        right--;
                    }
                }
            }
            i++;
            3.防止越界        
            while(i<nums.size() && nums[i-1]==nums[i])
            {
                i++;
            }
        }
        return ret;
    }
};

OJ（八）

18. 四数之和 - 力扣（LeetCode）

1）题目展示

2）解法思路

解法1：排序+暴力枚举+set去重（4个循环）

解法2：排序+双指针

1.依次固定一个数a（我们从最左边第一个数开始）

2.在a的后面的区间内，使用“三数之和“找到数，使这三个数的和等于target-a即可

3.那么，根据上面的三数之和题目我们知道：

->固定一个数b

->在b的后面区间，利用双指针找到两个数，使这两个数的和等于target-a-b即可

整体大概思路就完成了，

接下来我们来处理细节问题：

1.做到不漏：

解决：找到一种结果后，不要停，缩小区间，继续找

2.做到不重复

解决:

找到一种结果后，left和right都要跳过重复的数

当使用完一次双指针算法后，固定的数也要跳过重复的数。

此外，解决上面的问题的同时，还要注意避免越界的问题（代码中显示）

3）代码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        
        vector<vector<int>> ret;
        for(int a=0;a<n;)
        {
            for(int b=a+1;b<n;)
            {
                int left=b+1,right=n-1;
                long long aim=(long long)target-nums[a]-nums[b];
                while(left<right)
                {
                    if(nums[left]+nums[right]>aim)
                    {
                        right--;
                    }
                    else if(nums[left]+nums[right]<aim)
                    {
                        left++;
                    }
                    else
                    {
                        ret.push_back({nums[left],nums[right],nums[b],nums[a]});
                        left++;
                        while(left<right && nums[left]==nums[left-1])
                        {
                            left++;
                        }
                        right--;
                        while(left<right && nums[right+1]==nums[right])
                        {
                            right--;
                        }
                    }
                }
                ++b;
                while(b<n && nums[b]==nums[b-1])
                {
                    b++;
                }
            }

            ++a;
            while(a<n && nums[a]==nums[a-1])
            {
                a++;
            }
        }
        return ret;
    }
};

好了，双指针法专题到这里就分析完了，希望对你有所进步！

最后，到了本次鸡汤部分：

切勿轻言放弃，最好的东西，总会压轴出场！

相关文章：

  • 骨密度以及骨密度测量，测量方案，意义；提高；实现方案
  • 01背包问题和完全背包问题
  • Vite 开发服务器漏洞
  • PC名词解释-笔记本的S0,S1,S2,S3,S4,S5状态
  • 元宇宙浪潮下，数字孪生如何“乘风破浪”？
  • SQL Server 动态构建 SQL 语句学习指南
  • Redis 数据淘汰策略深度解析
  • Text2SQL推理类大模型本地部署的解决方案
  • 物质与空：边界中的确定性，虚无中的无限可能——跨学科视角下的存在本质探析
  • 启扬RK3568开发板已成功适配OpenHarmony4.0版本
  • Faster RCNN Pytorch 实现 代码级 详解
  • Android Kotlin 中使用 MPAndroidChart 绘制优雅的曲线图：封装与优化实践
  • 学习记录-Ajax-自封装axios函数
  • 【10】Strongswan collections —— array
  • 使用HTTP提交git时,每次都要输入用户名和密码的解决方案
  • 使用ZYNQ芯片和LVGL框架实现用户高刷新UI设计系列教程(第五讲)
  • 寻找重复数 - LeetCode 287 题解笔记
  • Linux 系统检测进程死锁的方法
  • 今日 GitHub 热门项目大赏，你 pick 谁？
  • 4.go语言数组
  • 佛山做网站需要多少钱/武汉seo优化顾问
  • 设计方案表网站名称/代哥seo
  • 网站建设空间申请/网站免费搭建平台
  • 网站布局技术/官网seo优化
  • 网站建设哪家服务好/深圳网站开发技术
  • 网站设计与网页制作/教育培训机构网站