BFS最短路径（十七）675. 为高尔夫比赛砍树 困难
675. 为高尔夫比赛砍树
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个
m x n的矩阵表示， 在这个矩阵中：
0表示障碍，无法触碰1表示地面，可以行走比 1 大的数表示有树的单元格，可以行走，数值表示树的高度每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为
1（即变为地面）。你将从
(0, 0)点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回-1。可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。
示例 1：
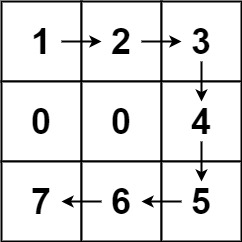
输入：forest = [[1,2,3],[0,0,4],[7,6,5]] 输出：6 解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。示例 2：
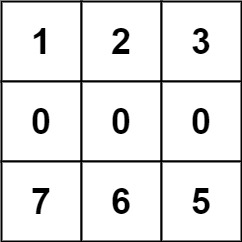
输入：forest = [[1,2,3],[0,0,0],[7,6,5]] 输出：-1 解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。示例 3：
输入：forest = [[2,3,4],[0,0,5],[8,7,6]] 输出：6 解释：可以按与示例 1 相同的路径来砍掉所有的树。 (0,0) 位置的树，可以直接砍去，不用算步数。提示：
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109
下图中，从0，0 位置的 1 出发 ，走到下方的2 再走到4 5 8 10 12 14这样
那么此题就转化为了俩俩坐标之间的迷宫问题，只需要求出每俩坐标之间最小的步数，最后把所有的步数加起来即可。
1、将给定的二维数组重新处理，使用一个Node结构体来进行存储，结构体内部有树高权值、以及树的横纵坐标。并且需要使用sort接口按照树高进行自定义排序。
sort函数对结构体自定义排序
class Node {
public:
int _key;
pair<int, int> _PII;
Node(int key, int i, int j) {
_key = key;
_PII.first = i;
_PII.second = j;
}
};
class Com {
public:
bool operator()(const Node& left, const Node& right) {
return left._key < right._key;
}
};
sort(v.begin(), v.end(), Com());2、每次bfs访问俩个坐标之间的最小步数
i j 表示 当前位置，t_x t_y 表示目标位置
进行bfs操作，将起始位置放入队列中，每轮将队列中所有一步能到达的位置加入队列，并进行判断处理。养成入队列进行操作的习惯。
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int m, n;
bool book[51][51] = {false};
int bfs(int i, int j, int t_x, int t_y,
vector<vector<int>>& forest) {
if(i == t_x && j == t_y)
return 0;
queue<pair<int, int>> q;
memset(book, 0, sizeof book);
int res = 0;
q.push({i, j});
book[i][j] = true;
while (q.size()) {
int size = q.size();
res++;
while (size--)
{
auto [a, b] = q.front();
q.pop();
for (int k = 0; k < 4; k++) {
int x = a + dx[k];
int y = b + dy[k];
if (x >= 0 && y >= 0 && x < m && y < n &&
forest[x][y] != 0 && !book[x][y]) {
if(x == t_x && y == t_y)
return res;
book[x][y] = true;
q.push({x, y});
}
}
}
}
return -1;
}3、调用bfs函数统计步数并求和
3、对排序好的树俩俩之间求出最短步数 把每一段之间的最短步数相加求和即为结果
int res = 0;
int bx = 0, by = 0;
for(auto &node : v)
{
int step = bfs(bx, by, node._PII.first, node._PII.second, forest);
if(step == -1)
return -1;
res += step;
bx = node._PII.first;
by = node._PII.second;
}
return res;class Node {
public:
int _key;
pair<int, int> _PII;
Node(int key, int i, int j) {
_key = key;
_PII.first = i;
_PII.second = j;
}
};
class Com {
public:
bool operator()(const Node& left, const Node& right) {
return left._key < right._key;
}
};
class Solution {
public:
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
int m, n;
bool book[51][51] = {false};
int bfs(int i, int j, int t_x, int t_y,
vector<vector<int>>& forest) {
if(i == t_x && j == t_y)
return 0;
queue<pair<int, int>> q;
memset(book, 0, sizeof book);
int res = 0;
q.push({i, j});
book[i][j] = true;
while (q.size()) {
int size = q.size();
res++;
while (size--)
{
auto [a, b] = q.front();
q.pop();
for (int k = 0; k < 4; k++) {
int x = a + dx[k];
int y = b + dy[k];
if (x >= 0 && y >= 0 && x < m && y < n &&
forest[x][y] != 0 && !book[x][y]) {
if(x == t_x && y == t_y)
return res;
book[x][y] = true;
q.push({x, y});
}
}
}
}
return -1;
}
int cutOffTree(vector<vector<int>>& forest) {
vector<Node> v;
m = forest.size(), n = forest[0].size();
1、将每棵树树高和坐标位置放入vector中
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (forest[i][j] > 1) {
v.push_back(Node(forest[i][j], i, j));
}
}
}
2、按照树高大小进行排序
sort(v.begin(), v.end(), Com());
3、对排序好的树俩俩之间求出最短步数 把每一段之间的最短步数相加求和即为结果
int res = 0;
int bx = 0, by = 0;
for(auto &node : v)
{
int step = bfs(bx, by, node._PII.first, node._PII.second, forest);
if(step == -1)
return -1;
res += step;
bx = node._PII.first;
by = node._PII.second;
}
return res;
}
};