哈希表和冲突处理
目录
前言
散列表
散列表的构造
直接定址法
除留余数法
如何选择
散列冲突
装填因子
冲突影响因素
冲突解决方法
线性探测法
查找
删除
平方探测(二次探测法)
查找
删除
拉链法
前言
哈希表也被称作为散列表,下面以散列表来表示
散列表
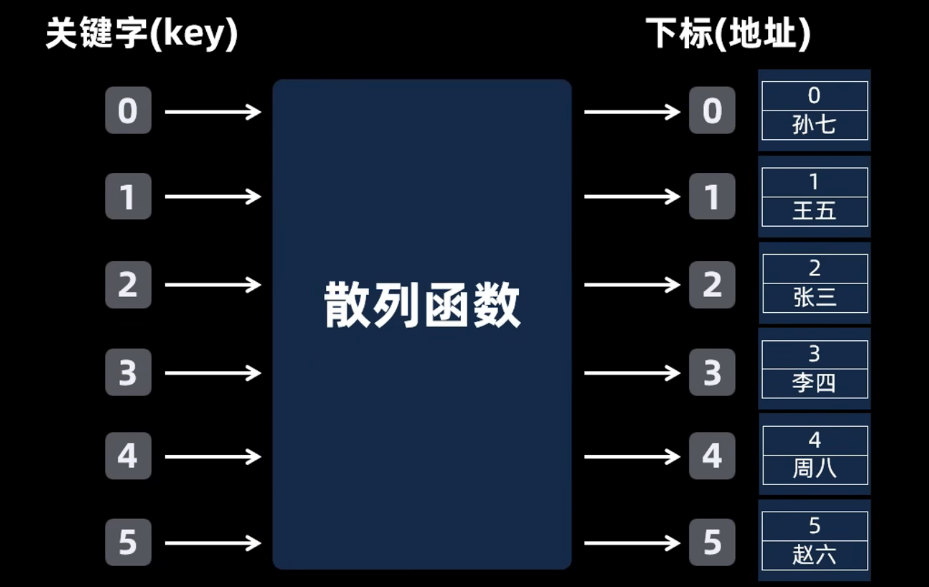
关键字通过一个函数与数组的下标形成某种映射关系,这种函数被称作为散列函数(哈希函数),这个数组称作为散列表,类似python中的字典。
例如:学生类中,以学号为关键字key,那么通过散列函数映射到数组中的下标,这就是散列表
散列表的构造
直接定址法
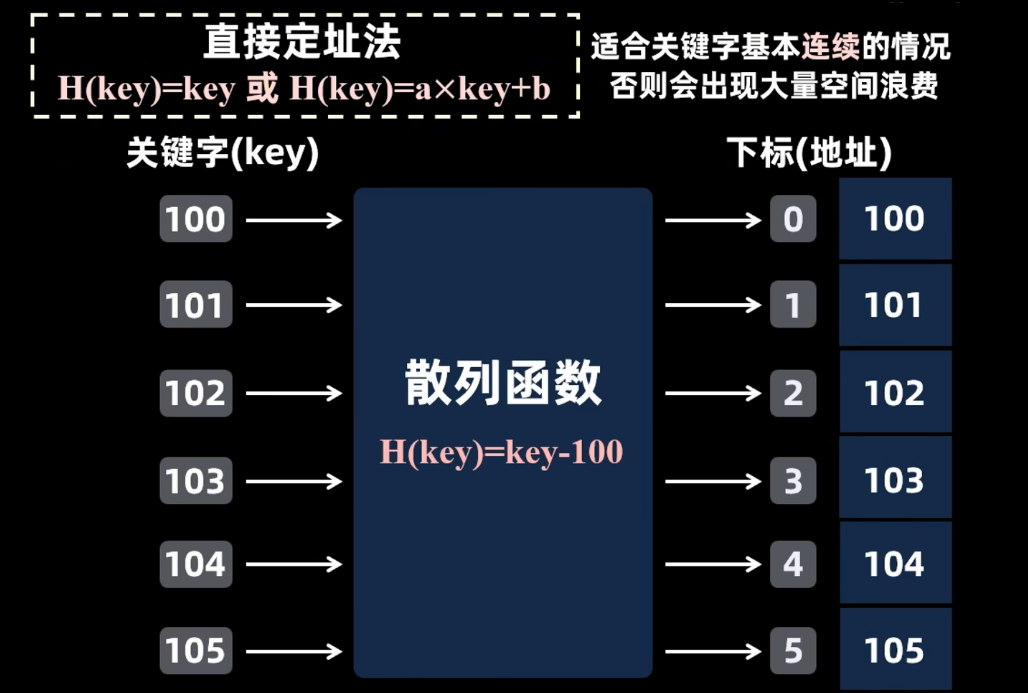
除留余数法
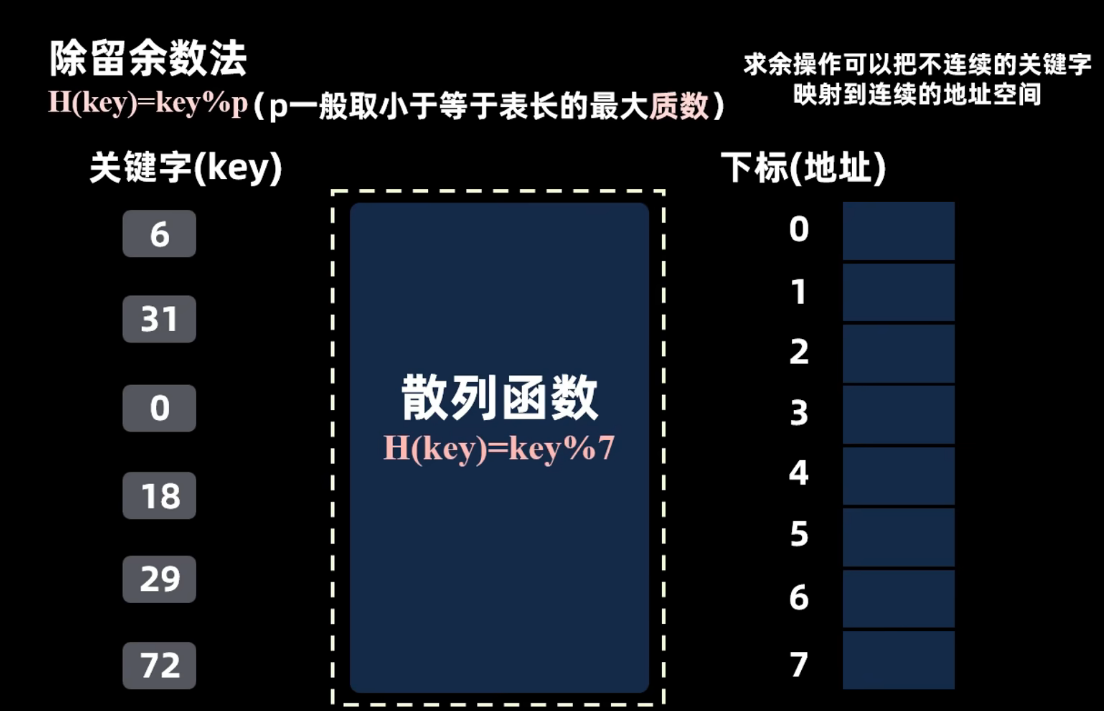
如何选择

散列冲突
装填因子

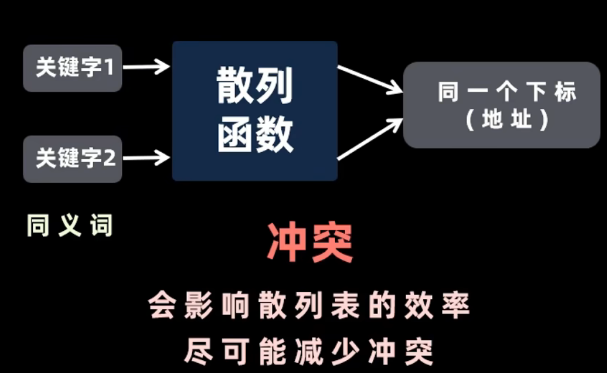
冲突影响因素
冲突:会影响散列表的效率,尽可能减少冲突,无法避免冲突
影响因素:散列函数、装填因子、处理冲突方式
冲突解决方法
线性探测法和二次探测法统称为开发地址法(再散列法)
基本思想是:当关键字key的哈希地址p=H(key)出现冲突时,以p为基础,产生另一个哈希地址p1,如果p1仍让冲突,再以p为基础,产生另一个哈希地址p2,……,直到找出一个不冲突的哈希地址pi,将相应元素存入其中。这种方法有一个通用的再散列函数形式:
Hi = ( H(key) + di ) % m 【i = 1,2,3,……,n】
其中 H(key) 为哈希函数,m为表长,di为增量序列。增量序列取值不同,相应的再散列方式也不同。除了线性探测法,二次探测法,还有伪随机探测再散列
线性探测法
冲突后依次探测下一个位置,直到遇到空闲位置。表尾的下一个位置是表首
问题:那么这样如果填满整个列表,岂不是会一直死循环下去?
回答:是的。但是我们一般不会填满整个列表,在装填因子大于0.75时候会扩充数组
查找

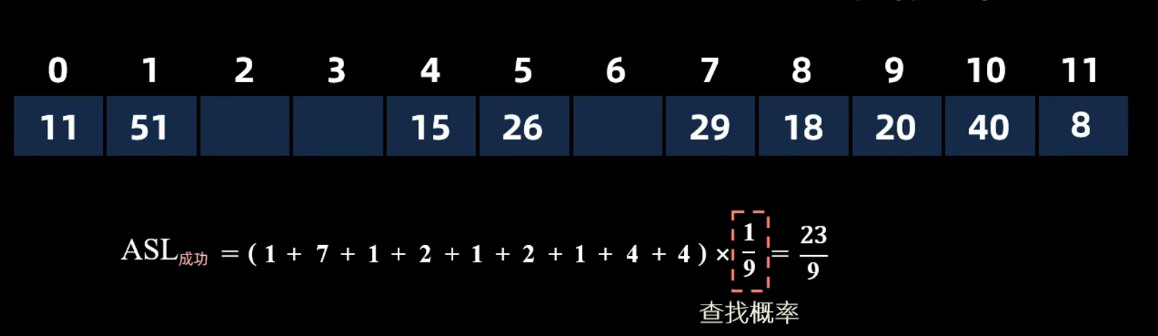
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #


删除
删除标记不影响查找和插入

平方探测(二次探测法)

查找
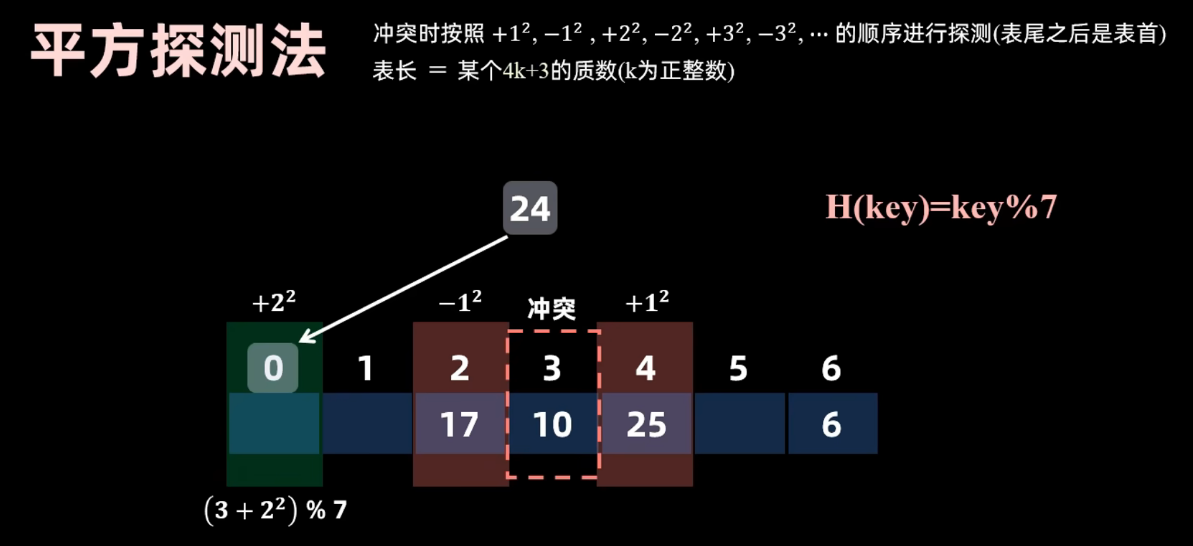
删除

伪随机探测再散列

di = 伪随机序列。具体实现时候,应该建立一个伪随机数发生器(如 i = (i+p) % m ),并给定一个随机数做起点
例如:已知散列表长度m=11,散列函数为:H(key) = key % 11,则H(47) = 3,H(60) = 5,假设下一个关键字为69,则H(69) = 3,与47冲突。
此时,伪随机数序列为2,5,9,……,则下一个散列地址为H1 = (3+2) % 11 = 5,仍然冲突,再找下一个哈希地址H2 = (3+5) % 11 = 8,此时不冲突,将69填入8号单元。
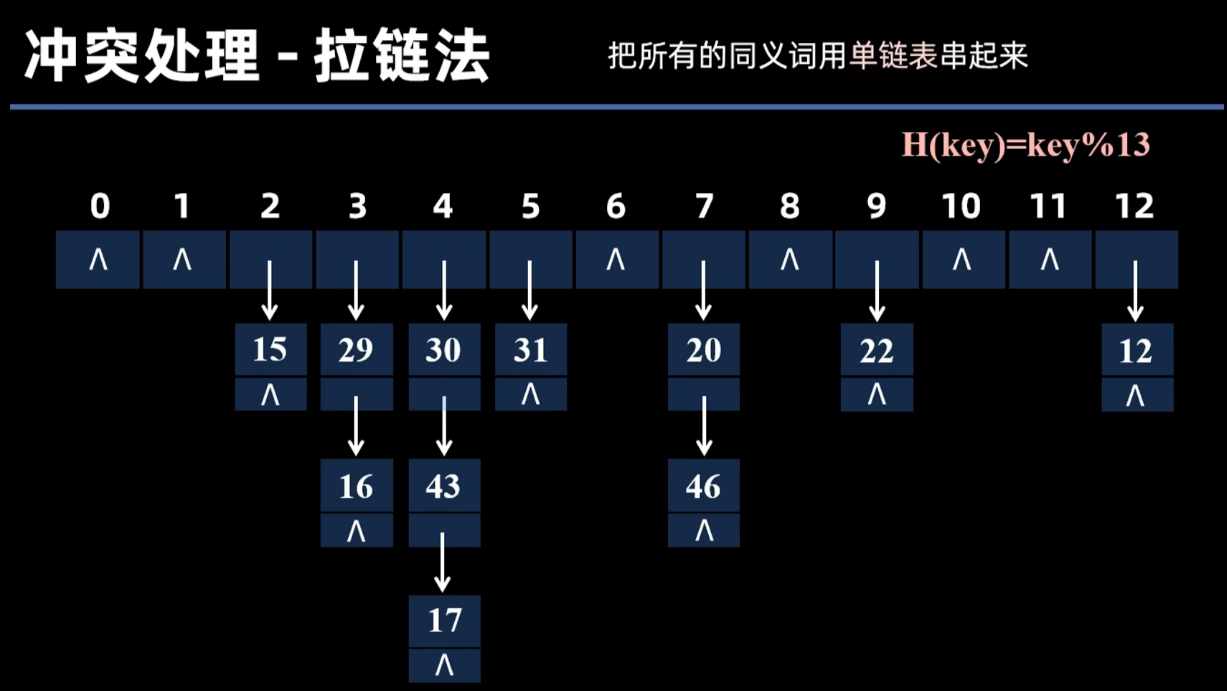
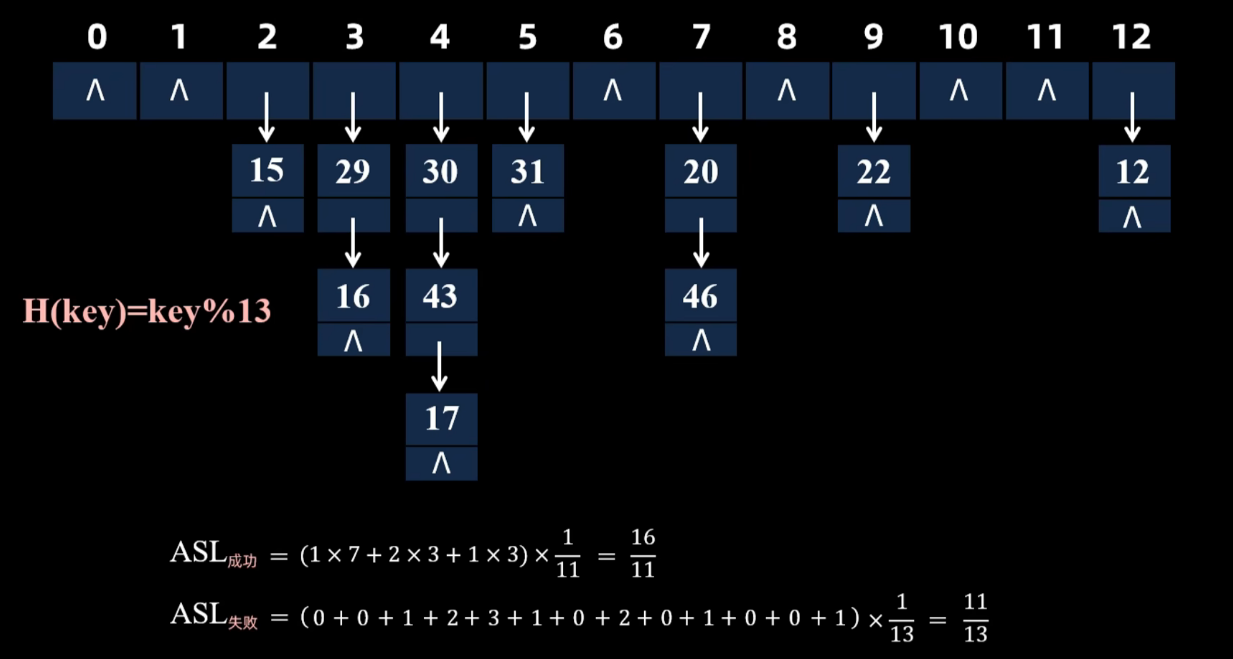
拉链法
把所以映射到同一个位置(同义词)的关键字用链表串起来