算法奇妙屋(十二)-优先级队列(堆)

一. 力扣 1046. 最后一块石头的重量

1. 题目

2. 算法原理

这道题的算法原理十分简单, 直接建立大根堆即可, 这里简单梳理下

3. 代码

    public int lastStoneWeight(int[] stones) {PriorityQueue<Integer> queue = new PriorityQueue<>((a,b) -> b - a);for (int x : stones) {queue.offer(x);}while (queue.size() > 1) {int max1 = queue.poll();int max2 = queue.poll();if (max1 > max2) {queue.offer(max1 - max2);}}if (!queue.isEmpty()) {return queue.poll();}else {return 0;}}

---

二. 力扣 703. 数据流中的第 K 大元素

1. 题目

题目意思简单易懂, 这里不过多赘述, 直接看图即可

2. 算法原理

这道题有点绕口, 这里我们在初始化类的时候先求出来topk, 然后在后台调用add方法的时候, 只需要重复求topk流程即可, 下面图片解析的是求topk问题时,应该建立哪种类型的堆, 为什么要建这种堆?

3. 代码

    PriorityQueue<Integer> q;int t_k;public KthLargest(int k, int[] nums) {q = new PriorityQueue<>();t_k = k;for (int x : nums) {q.offer(x);if (q.size() > t_k) {q.poll();}}}public int add(int val) {q.offer(val);if (q.size() > t_k) {q.poll();}return q.peek();}

---

三. 力扣 692. 前K个高频单词

1. 题目

2. 算法原理

这道题原理不难, 难的是如何将代码实现, 注意掌握Pair的特性

3. 代码

    public List<String> topKFrequent(String[] words, int k) {Map<String, Integer> hash = new HashMap<>();for (String s : words) {hash.put(s, hash.getOrDefault(s, 0) + 1);}PriorityQueue<Pair<String, Integer>> q = new PriorityQueue<>((a, b) -> {if (a.getValue().equals(b.getValue())) {return b.getKey().compareTo(a.getKey());}else {return a.getValue() - b.getValue();}});for (Map.Entry<String, Integer> e : hash.entrySet()) {q.offer(new Pair<>(e.getKey(), e.getValue()));if (q.size() > k) {q.poll();}}List<String> ret = new ArrayList<>();while (!q.isEmpty()) {ret.add(q.poll().getKey());}Collections.reverse(ret);return ret;}

---

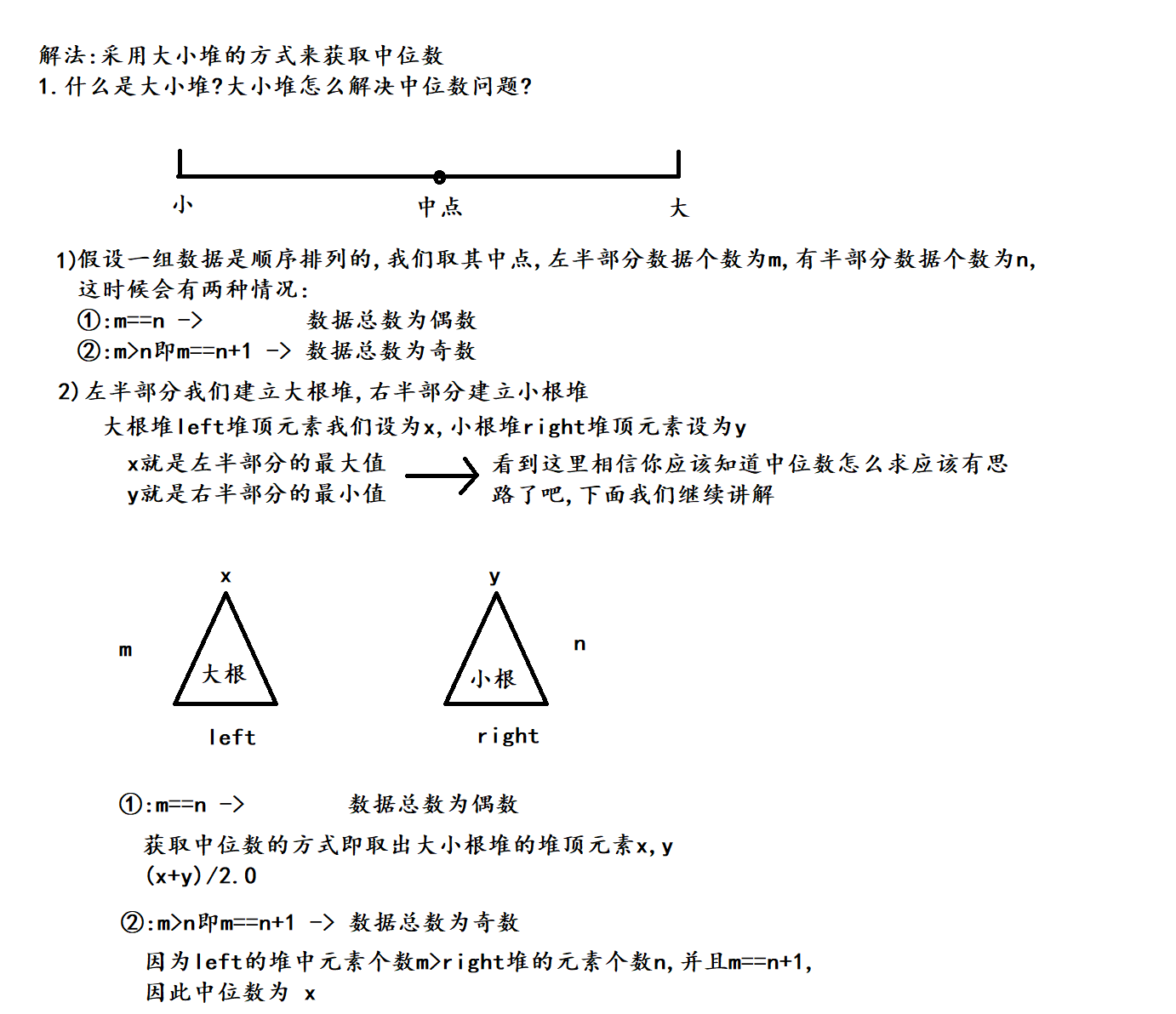
四. 力扣 295. 数据流的中位数

1. 题目

题目就是让求中位数, 最后结果需要注意是double类型

2. 算法原理

(1) 我们这里采用大小堆的解法, 下面我们来解释什么是大小堆

(2)一些细节问题, 例如如何入堆?如何维护顺序排列的数据流?

3. 代码

    PriorityQueue<Integer> left;PriorityQueue<Integer> right;public MedianFinder() {left = new PriorityQueue<>((a, b) -> b - a);right = new PriorityQueue<>();}public void addNum(int num) {int m = left.size();int n = right.size();Integer x = left.peek();if (m == n) {if (x == null) {left.offer(num);} else if (num <= x) {left.offer(num);} else {right.offer(num);left.offer(right.poll());}} else {if (num <= x) {left.offer(num);x = left.poll();right.offer(x);}else {right.offer(num);}}}public double findMedian() {if (left.size() == right.size()) {return (left.peek() + right.peek()) / 2.0;}else {return left.peek();}}