力扣-二叉树的前序遍历

核心思路

前序遍历（Pre-order Traversal）是二叉树遍历的一种基础方式，其核心思路是按照 **“根节点 -> 左子树 -> 右子树”** 的顺序，递归地访问树中的每一个节点。

这个过程可以自然地通过函数递归来实现，因为：

1. 访问当前节点。

2. 对当前节点的左子树执行同样的前序遍历操作。

3. 对当前节点的右子树执行同样的前序遍历操作。

当遇到空节点时，递归操作终止，这构成了递归的终止条件。

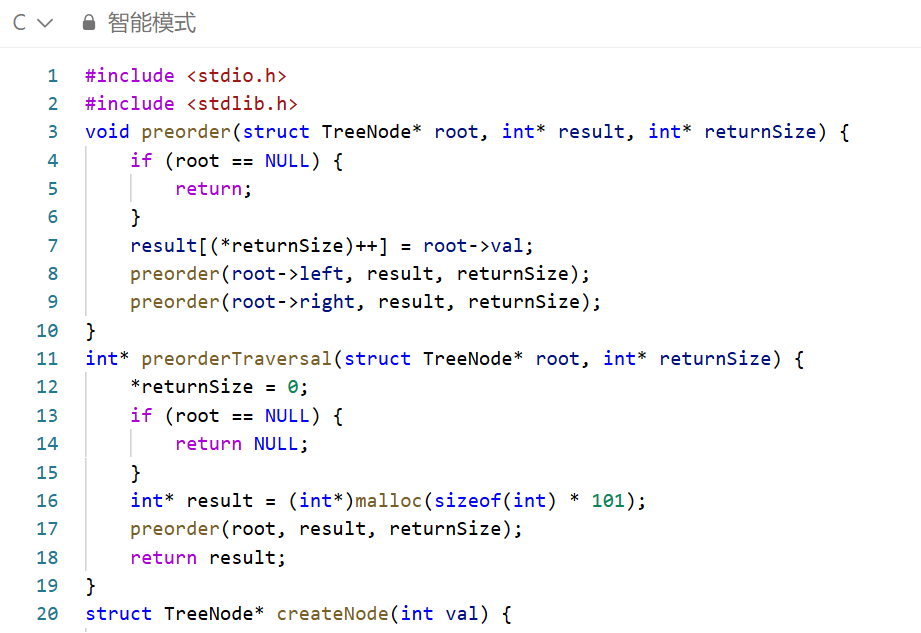
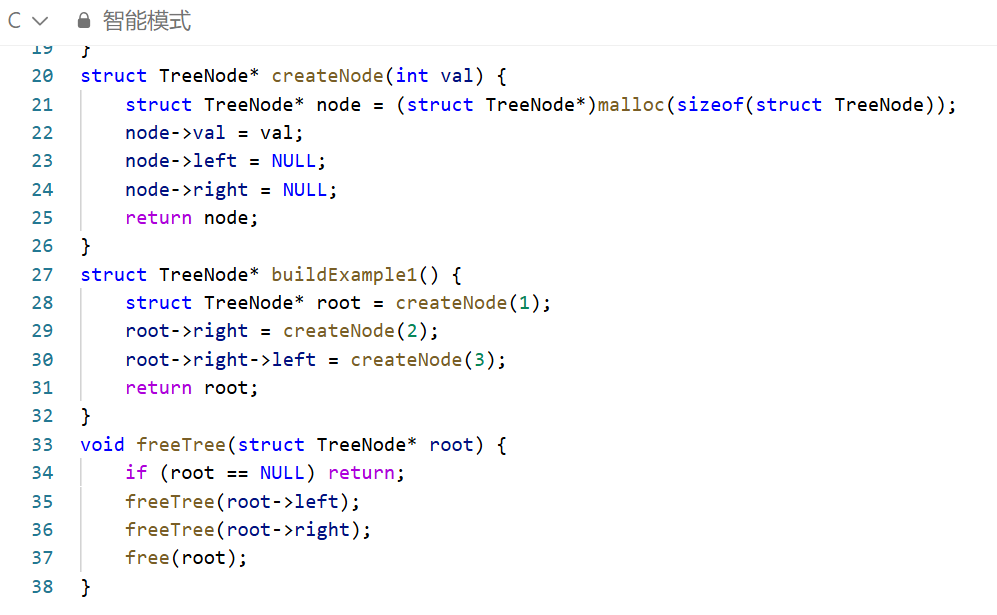
方法（递归法）

递归法是实现前序遍历最直观、最简洁的方法。

1. 设计递归函数：定义一个辅助递归函数，它接收三个参数：当前遍历的根节点 `root`、用于存储遍历结果的数组 `result`、以及一个用于记录结果数组大小的指针 `returnSize`。

2. 确定递归终止条件：在递归函数内部，首先检查当前节点 `root` 是否为 `NULL`。如果是，则直接返回，不进行任何操作。

3. 定义递归过程：如果当前节点不为空，就访问该节点。在这个问题中，“访问”意味着将节点的值 `root->val` 存入结果数组 `result` 中，并将数组大小 `returnSize` 加一。然后，递归调用该函数，遍历当前节点的左子树。最后，递归调用该函数，遍历当前节点的右子树。

4. 主函数操作：在主函数 `preorderTraversal` 中，首先处理边界情况（空树）。为结果数组分配足够的内存（根据题目提示，节点数最多为100）。初始化结果数组大小 `returnSize` 为0。调用辅助递归函数，开始遍历。返回填充好的结果数组。

优点

使用递归法实现前序遍历具有以下显著优点：

1. 代码简洁优雅：代码逻辑直接反映了前序遍历的定义（根->左->右），非常容易理解和编写。几行核心代码就能完成复杂的遍历操作。

2. 可读性极高：递归的自相似性使得代码的意图一目了然，降低了沟通和维护的成本。

3. 符合直觉：树本身就是一种递归定义的数据结构，用递归的方式去操作它是最自然、最符合直觉的。

结论

1. 正确性：递归法完全正确地实现了前序遍历的逻辑，能够按照“根节点 -> 左子树 -> 右子树”的顺序访问所有节点。

2. 高效性：

时间复杂度: O(n)，其中 `n` 是树中节点的总数。每个节点都需要被访问一次，递归函数的调用次数与节点数成正比。

空间复杂度: O(h)，其中 `h` 是树的高度。空间复杂度主要由递归调用栈的深度决定。在最坏的情况下（例如，一棵退化成链表的树），树的高度 `h` 等于节点数 `n`，此时空间复杂度为 O(n)。对于平衡二叉树，空间复杂度为 O(log n)。

3. 适用性：递归法是解决树遍历问题的标准方法和首选方法，特别适用于面试和日常开发等场景。它充分利用了计算机的函数调用栈，将复杂的问题分解为更小的子问题，是分治思想的典型应用。

4. 总结：对于二叉树的前序遍历，递归法是最直观、最简洁、也是最推荐的方法。它完美地平衡了代码复杂度和可读性，是处理树结构问题的强大工具。