三级供应链竞合博弈模拟
这是一个三级供应链博弈模拟系统的完整代码实现,基于郭红莲等人(2008)的研究模型。让我深度解读这个复杂系统的各个组成部分:
概述
1. 核心模型结构
# 三级供应链网络:M个供应商 → 1个制造商 → N个经销商
# 资金流:经销商 ← 制造商 ← 供应商
# 物流:供应商 → 制造商 → 经销商2. 关键技术实现
中文显示支持
def setup_chinese_font():# 跨平台字体配置,解决matplotlib中文显示问题# Windows: SimHei, macOS: Heiti SC, Linux: WenQuanYi自动检测操作系统并配置相应中文字体
设置Agg后端避免GUI冲突
供应链博弈模型
class SupplyChainGame:# 核心经济参数self.w = 1000 # 产品售价self.c_m = 500 # 制造成本self.D_bar = 100000 # 基准需求数学模型
1. 需求函数模型
def demand_function(self, I_r):"""D(I_r) = D_bar + a1 × I_r^b1"""return self.D_bar + self.a1 * (I_r ** self.b1)经济学意义:促销投资I_r的边际收益递减
参数含义:a1-需求敏感性,b1-需求弹性(0<b1<1)
2. 成本函数模型
def cost_function(self, I_s, D):"""c(I_s) = c_bar - a2 × (I_s/D)^b2"""return self.c_bar - self.a2 * ((I_s / D) ** self.b2)规模经济效应:研发投资I_s通过产量D分摊降低成本
技术溢出:b2控制成本降低的边际效果
3. 三种决策模式对比
集中决策(理想基准)
def centralized_profit(self, investments):# 供应链整体利润最大化profit = D × (w - c_m - c) - I_r - I_s最优解:通过
scipy.optimize.minimize求解意义:供应链协同的理论上限
分散决策(现实博弈)
# 经销商利润:(w - w1)×D_i - (1-s1)×I_ri
# 供应商利润:(w2 - c)×D_j - (1-s2)×I_sj
# 制造商利润:(w1 - c_m - w2)×D + s1×I_r + s2×I_s双重边际效应:各级独立决策导致整体效率损失
纳什均衡:通过对称性假设简化计算
协调优化(契约设计)
def find_optimal_contract(self, M, N):# 网格搜索最优契约参数(w1, s1, w2, s2)协调机制:通过批发价+补贴率激励合作
目标:逼近集中决策效率
可视化与交互
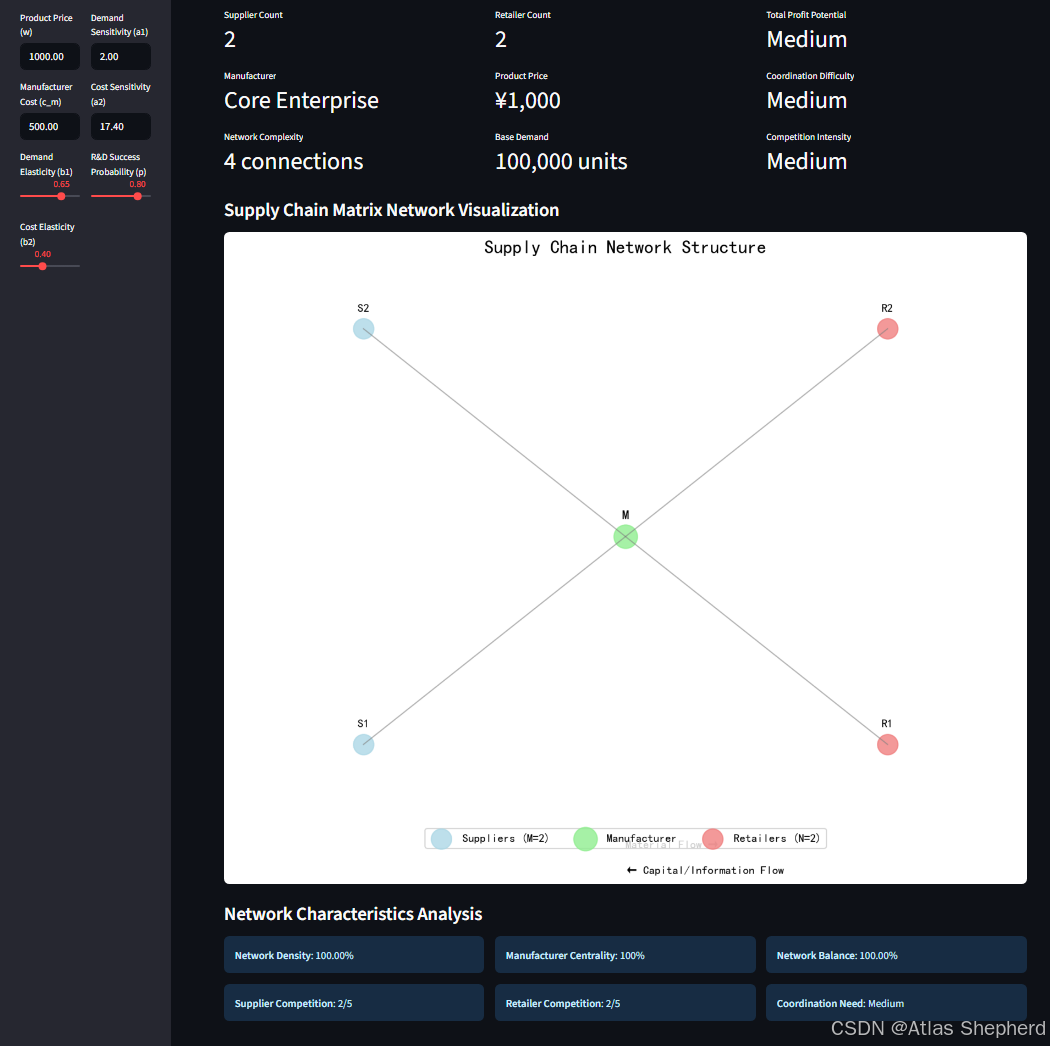
1. 网络结构可视化
def create_matrix_network_visualization(M, N):# 动态生成供应链网络图# 节点位置计算、连线关系、标签标注直观展示M×N复杂网络结构
实时反映参数变化对网络密度的影响
2. 多维度分析面板
敏感性分析
促销投资对系统利润的边际影响
研发投资对成本降低的效果曲线
利润分布分析
饼图显示三级利润分配比例
柱状图对比各参与方收益
协调效果评估
# 协调效率 = 协调后利润 / 集中决策利润
coordination_efficiency = optimal_result['total_profit'] / ideal_profit系统特色与创新点
1. 理论实践结合
将复杂博弈论模型转化为可操作模拟系统
参数可调,支持what-if分析
2. 算法优化
# 对称均衡假设大幅降低计算复杂度
# 从O(M×N)降到O(1)的优化问题
I_r_total = N × I_r_sym
I_s_total = M × I_s_sym3. 用户体验设计
渐进式披露:从概览到细节的四标签页设计
实时反馈:参数调整立即反映在可视化结果中
性能平衡:网格搜索与近似计算兼顾精度与速度
代码
import streamlit as st
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import minimize
import warnings
import sys
import oswarnings.filterwarnings('ignore')# 解决中文字符显示问题
def setup_chinese_font():"""设置中文字体支持"""try:# 尝试使用系统中常见的中文字体if sys.platform.startswith('win'): # Windows系统plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']elif sys.platform.startswith('darwin'): # macOS系统plt.rcParams['font.sans-serif'] = ['Heiti SC', 'STHeiti', 'DejaVu Sans']else: # Linux系统plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei', 'DejaVu Sans']plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 设置matplotlib后端,避免GUI相关的问题plt.switch_backend('Agg')except Exception as e:st.warning(f"字体设置遇到问题: {e}, 使用默认字体")# 初始化字体设置
setup_chinese_font()class SupplyChainGame:def __init__(self):# 默认参数(基于文档中的手机供应链案例)self.w = 1000 # 产品售价self.c_m = 500 # 制造商生产成本self.D_bar = 100000 # 基准需求self.c_bar = 339.7 # 基准成本# 需求函数参数self.a1 = 2self.b1 = 0.65# 成本函数参数self.a2 = 17.4self.b2 = 0.4# 研发成功概率self.p = 0.8def demand_function(self, I_r):"""需求函数:D(I_r) = D_bar + a1 * I_r^b1"""return self.D_bar + self.a1 * (I_r ** self.b1)def cost_function(self, I_s, D):"""成本函数:c(I_s) = c_bar - a2 * (I_s/D)^b2"""if D <= 0 or I_s <= 0:return self.c_barreturn self.c_bar - self.a2 * ((I_s / D) ** self.b2)def centralized_profit(self, investments):"""集中决策下的系统利润函数"""I_r, I_s = investmentsD = self.demand_function(I_r)c = self.cost_function(I_s, D)if I_r < 0 or I_s < 0:return -np.infprofit = D * (self.w - self.c_m - c) - I_r - I_sreturn -profit # 负号因为我们要最小化负利润def decentralized_retailer_profit(self, I_ri, I_r_total, w1, s1):"""经销商利润函数"""if I_r_total <= 0:return 0market_share = I_ri / I_r_totalD_total = self.demand_function(I_r_total)D_i = market_share * D_totalprofit = (self.w - w1) * D_i - (1 - s1) * I_rireturn profitdef decentralized_supplier_profit(self, I_sj, I_s_total, I_r_total, w2, s2):"""供应商利润函数"""if I_s_total <= 0:return 0order_share = I_sj / I_s_totalD_total = self.demand_function(I_r_total)D_j = order_share * D_totalc = self.cost_function(I_s_total, D_total)profit = (w2 - c) * D_j - (1 - s2) * I_sjreturn profit * self.p # 考虑研发成功概率def find_nash_equilibrium(self, M, N, w1, s1, w2, s2):"""寻找纳什均衡投资水平"""# 对称均衡假设下,所有供应商投资相同,所有经销商投资相同def equilibrium_profit(investments):I_r_sym, I_s_sym = investmentsI_r_total = N * I_r_symI_s_total = M * I_s_symretailer_profit = self.decentralized_retailer_profit(I_r_sym, I_r_total, w1, s1)supplier_profit = self.decentralized_supplier_profit(I_s_sym, I_s_total, I_r_total, w2, s2)# 最大化总利润(在对称均衡中)return -(retailer_profit + supplier_profit)# 初始猜测x0 = [10000, 5000]bounds = [(0, None), (0, None)]result = minimize(equilibrium_profit, x0, bounds=bounds, method='L-BFGS-B')if result.success:I_r_sym, I_s_sym = result.xI_r_total = N * I_r_symI_s_total = M * I_s_symD_total = self.demand_function(I_r_total)c = self.cost_function(I_s_total, D_total)# 计算各方利润retailer_profit = N * self.decentralized_retailer_profit(I_r_sym, I_r_total, w1, s1)supplier_profit = M * self.decentralized_supplier_profit(I_s_sym, I_s_total, I_r_total, w2, s2)manufacturer_profit = D_total * (w1 - self.c_m - w2) + s1 * I_r_total + s2 * I_s_totaltotal_profit = retailer_profit + supplier_profit + manufacturer_profitreturn {'I_r_total': I_r_total,'I_s_total': I_s_total,'D_total': D_total,'c': c,'retailer_profit': retailer_profit,'supplier_profit': supplier_profit,'manufacturer_profit': manufacturer_profit,'total_profit': total_profit}else:return Nonedef find_optimal_contract(self, M, N):"""寻找最优协调契约参数"""best_result = Nonebest_total_profit = -np.infbest_params = {}# 搜索最优契约参数空间for w1 in np.linspace(900, 1000, 11):for s1 in np.linspace(0, 1, 6):for w2 in np.linspace(300, 340, 9):for s2 in np.linspace(0, 1, 6):result = self.find_nash_equilibrium(M, N, w1, s1, w2, s2)if result and result['total_profit'] > best_total_profit:best_total_profit = result['total_profit']best_result = resultbest_params = {'w1': w1, 's1': s1, 'w2': w2, 's2': s2}return best_result, best_paramsdef create_matrix_network_visualization(M, N):"""创建矩阵网络可视化"""fig, ax = plt.subplots(figsize=(12, 8))# 定义节点位置supplier_x = np.ones(M) * 1supplier_y = np.linspace(0.1, 0.9, M)manufacturer_x = np.ones(1) * 2manufacturer_y = np.array([0.5])retailer_x = np.ones(N) * 3retailer_y = np.linspace(0.1, 0.9, N)# 绘制节点ax.scatter(supplier_x, supplier_y, s=300, c='lightblue', alpha=0.8, label=f'Suppliers (M={M})')ax.scatter(manufacturer_x, manufacturer_y, s=400, c='lightgreen', alpha=0.8, label='Manufacturer')ax.scatter(retailer_x, retailer_y, s=300, c='lightcoral', alpha=0.8, label=f'Retailers (N={N})')# 绘制连接线for i in range(M):ax.plot([supplier_x[i], manufacturer_x[0]], [supplier_y[i], manufacturer_y[0]],'gray', alpha=0.6, linewidth=1)for j in range(N):ax.plot([manufacturer_x[0], retailer_x[j]], [manufacturer_y[0], retailer_y[j]],'gray', alpha=0.6, linewidth=1)# 添加节点标签for i in range(M):ax.text(supplier_x[i], supplier_y[i] + 0.03, f'S{i + 1}',ha='center', va='bottom', fontsize=10, fontweight='bold')ax.text(manufacturer_x[0], manufacturer_y[0] + 0.03, 'M',ha='center', va='bottom', fontsize=12, fontweight='bold')for j in range(N):ax.text(retailer_x[j], retailer_y[j] + 0.03, f'R{j + 1}',ha='center', va='bottom', fontsize=10, fontweight='bold')# 设置图形属性ax.set_xlim(0.5, 3.5)ax.set_ylim(0, 1)ax.set_title('Supply Chain Network Structure', fontsize=16, fontweight='bold', pad=20)ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05), ncol=3)ax.axis('off')# 添加网络流说明ax.text(0.5, -0.1, 'Material Flow →', fontsize=10, ha='left', transform=ax.transAxes)ax.text(0.5, -0.15, '← Capital/Information Flow', fontsize=10, ha='left', transform=ax.transAxes)return figdef main():st.set_page_config(page_title="Supply Chain Game Simulation", layout="wide")st.title("📊 Three-Level Supply Chain Game Simulation System")st.markdown("Based on Guo Honglian et al. (2008) M-supplier-1-manufacturer-N-retailer supply chain model")# 初始化模型model = SupplyChainGame()# 侧边栏参数设置st.sidebar.header("🔧 Model Parameter Settings")col1, col2 = st.sidebar.columns(2)with col1:M = st.slider("Supplier Count (M)", 1, 100, 2)N = st.slider("Retailer Count (N)", 1, 100, 2)model.w = st.number_input("Product Price (w)", value=1000.0)model.c_m = st.number_input("Manufacturer Cost (c_m)", value=500.0)with col2:model.D_bar = st.number_input("Base Demand (D_bar)", value=100000.0)model.c_bar = st.number_input("Base Cost (c_bar)", value=339.7)model.a1 = st.number_input("Demand Sensitivity (a1)", value=2.0)model.a2 = st.number_input("Cost Sensitivity (a2)", value=17.4)col3, col4 = st.sidebar.columns(2)with col3:model.b1 = st.slider("Demand Elasticity (b1)", 0.1, 0.9, 0.65, 0.05)model.b2 = st.slider("Cost Elasticity (b2)", 0.1, 0.9, 0.4, 0.05)with col4:model.p = st.slider("R&D Success Probability (p)", 0.1, 1.0, 0.8, 0.1)# 主内容区域tab1, tab2, tab3, tab4 = st.tabs(["🏠 System Overview", "📈 Centralized Decision", "🤝 Decentralized Game", "⚖️ Coordination Optimization"])with tab1:st.header("Supply Chain System Overview")col1, col2, col3 = st.columns(3)with col1:st.metric("Supplier Count", M)st.metric("Manufacturer", "Core Enterprise")st.metric("Network Complexity", f"{M * N} connections")with col2:st.metric("Retailer Count", N)st.metric("Product Price", f"¥{model.w:,.0f}")st.metric("Base Demand", f"{model.D_bar:,.0f} units")with col3:st.metric("Total Profit Potential", "High" if M * N > 10 else "Medium")st.metric("Coordination Difficulty", "High" if M + N > 10 else "Medium")st.metric("Competition Intensity", "High" if M > 5 or N > 5 else "Medium")# 供应链矩阵网络结构图st.subheader("Supply Chain Matrix Network Visualization")fig = create_matrix_network_visualization(M, N)st.pyplot(fig)# 网络特性分析st.subheader("Network Characteristics Analysis")col1, col2, col3 = st.columns(3)with col1:st.info(f"**Network Density**: {M * N / (M * N) if M * N > 0 else 0:.2%}")st.info(f"**Supplier Competition**: {M}/5")with col2:st.info(f"**Manufacturer Centrality**: 100%")st.info(f"**Retailer Competition**: {N}/5")with col3:efficiency = min(M, N) / max(M, N) if max(M, N) > 0 else 0st.info(f"**Network Balance**: {efficiency:.2%}")st.info(f"**Coordination Need**: {'High' if efficiency < 0.5 else 'Medium'}")with tab2:st.header("Centralized Decision Model Analysis")st.markdown("**Ideal Scenario: Supply chain as a whole makes decisions**")# 集中决策优化result = minimize(model.centralized_profit, [10000, 5000],bounds=[(0, None), (0, None)], method='L-BFGS-B')if result.success:I_r_opt, I_s_opt = result.xD_opt = model.demand_function(I_r_opt)c_opt = model.cost_function(I_s_opt, D_opt)profit_opt = -result.funcol1, col2, col3, col4 = st.columns(4)col1.metric("Optimal Promotion Investment", f"¥{I_r_opt:,.0f}")col2.metric("Optimal R&D Investment", f"¥{I_s_opt:,.0f}")col3.metric("Optimal Demand", f"{D_opt:,.0f} units")col4.metric("System Optimal Profit", f"¥{profit_opt:,.0f}")# 敏感性分析st.subheader("Investment Sensitivity Analysis")I_r_range = np.linspace(0, 2 * I_r_opt, 50)profits = []for I_r in I_r_range:# 固定促销投资,优化研发投资res = minimize(lambda I_s: model.centralized_profit([I_r, I_s[0]]),[I_s_opt], bounds=[(0, None)], method='L-BFGS-B')if res.success:profits.append(-res.fun)else:profits.append(0)fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))ax1.plot(I_r_range, profits)ax1.axvline(I_r_opt, color='red', linestyle='--', alpha=0.7, label='Optimal Investment')ax1.set_xlabel('Promotion Investment I_r')ax1.set_ylabel('System Profit')ax1.set_title('Impact of Promotion Investment on System Profit')ax1.legend()ax1.grid(True, alpha=0.3)# 成本降低效果I_s_range = np.linspace(0, 2 * I_s_opt, 50)cost_reductions = [model.c_bar - model.cost_function(I_s, D_opt) for I_s in I_s_range]ax2.plot(I_s_range, cost_reductions)ax2.axvline(I_s_opt, color='red', linestyle='--', alpha=0.7, label='Optimal Investment')ax2.set_xlabel('R&D Investment I_s')ax2.set_ylabel('Cost Reduction')ax2.set_title('Impact of R&D Investment on Cost Reduction')ax2.legend()ax2.grid(True, alpha=0.3)st.pyplot(fig)else:st.error("Centralized decision optimization failed, please adjust parameters")with tab3:st.header("Decentralized Game Simulation")st.markdown("**Real Scenario: Independent decision-making with competition**")# 契约参数设置st.subheader("Contract Parameter Settings")col1, col2, col3, col4 = st.columns(4)with col1:w1 = st.slider("Wholesale Price (w1)", 800.0, 1000.0, 945.0)with col2:s1 = st.slider("Promotion Subsidy Rate (s1)", 0.0, 1.0, 0.5)with col3:w2 = st.slider("Procurement Price (w2)", 300.0, 400.0, 320.0)with col4:s2 = st.slider("R&D Subsidy Rate (s2)", 0.0, 1.0, 0.3)if st.button("Run Decentralized Simulation"):with st.spinner("Calculating Nash Equilibrium..."):result = model.find_nash_equilibrium(M, N, w1, s1, w2, s2)if result:st.success("Game equilibrium calculation completed!")col1, col2, col3, col4 = st.columns(4)col1.metric("Total Promotion Investment", f"¥{result['I_r_total']:,.0f}")col2.metric("Total R&D Investment", f"¥{result['I_s_total']:,.0f}")col3.metric("Market Demand", f"{result['D_total']:,.0f} units")col4.metric("Unit Cost", f"¥{result['c']:,.2f}")# 利润分布st.subheader("Profit Distribution Analysis")profits_data = {'Participant': ['Total Retailer Profit', 'Total Supplier Profit', 'Manufacturer Profit','Total System Profit'],'Profit (10k Yuan)': [result['retailer_profit'] / 10000,result['supplier_profit'] / 10000,result['manufacturer_profit'] / 10000,result['total_profit'] / 10000]}fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# 利润分布饼图labels = ['Retailers', 'Suppliers', 'Manufacturer']sizes = [result['retailer_profit'],result['supplier_profit'],result['manufacturer_profit']]ax1.pie(sizes, labels=labels, autopct='%1.1f%%', startangle=90)ax1.set_title('Profit Distribution Ratio')# 利润柱状图positions = range(len(profits_data['Participant']))ax2.bar(positions, profits_data['Profit (10k Yuan)'],color=['lightcoral', 'lightblue', 'lightgreen', 'gold'])ax2.set_xlabel('Participant')ax2.set_ylabel('Profit (10k Yuan)')ax2.set_title('Profit Comparison by Participant')ax2.set_xticks(positions)ax2.set_xticklabels(profits_data['Participant'], rotation=45)st.pyplot(fig)# 显示详细数据st.dataframe(pd.DataFrame(profits_data), width='stretch')else:st.error("Decentralized equilibrium calculation failed, please adjust parameters")with tab4:st.header("Coordination Contract Optimization")st.markdown("**Manufacturer coordinates supply chain through pricing and subsidy strategies**")if st.button("Find Optimal Coordination Contract", type="primary"):with st.spinner("Searching optimal contract parameter space..."):optimal_result, optimal_params = model.find_optimal_contract(M, N)if optimal_result:st.success("Optimal coordination contract found!")st.subheader("Optimal Contract Parameters")col1, col2, col3, col4 = st.columns(4)col1.metric("Optimal Wholesale Price", f"¥{optimal_params['w1']:.1f}")col2.metric("Optimal Promotion Subsidy", f"{optimal_params['s1']:.2%}")col3.metric("Optimal Procurement Price", f"¥{optimal_params['w2']:.1f}")col4.metric("Optimal R&D Subsidy", f"{optimal_params['s2']:.2%}")st.subheader("Post-Coordination Performance")col1, col2, col3, col4 = st.columns(4)col1.metric("Total System Profit", f"¥{optimal_result['total_profit']:,.0f}")col2.metric("Supply Chain Efficiency","High" if optimal_result['total_profit'] > 20000000 else "Medium")col3.metric("Market Demand", f"{optimal_result['D_total']:,.0f} units")col4.metric("Cost Efficiency", f"¥{optimal_result['c']:.1f}")# 协调效果分析st.subheader("Coordination Effect Analysis")# 计算集中决策最优值作为基准centralized_result = minimize(model.centralized_profit, [10000, 5000],bounds=[(0, None), (0, None)], method='L-BFGS-B')if centralized_result.success:ideal_profit = -centralized_result.funcoordination_efficiency = optimal_result['total_profit'] / ideal_profit# 协调效果对比分析st.markdown("#### Pre vs Post Coordination Comparison")# 模拟非协调情况(固定契约参数)fixed_params = {'w1': 945, 's1': 0.5, 'w2': 320, 's2': 0.3}fixed_result = model.find_nash_equilibrium(M, N, **fixed_params)if fixed_result:comparison_data = {'Metric': ['Total System Profit (10k Yuan)', 'Market Demand (units)', 'Unit Cost (Yuan)','Coordination Efficiency'],'Pre-Coordination': [fixed_result['total_profit'] / 10000,fixed_result['D_total'],fixed_result['c'],fixed_result['total_profit'] / ideal_profit],'Post-Coordination': [optimal_result['total_profit'] / 10000,optimal_result['D_total'],optimal_result['c'],coordination_efficiency],'Improvement %': [(optimal_result['total_profit'] - fixed_result['total_profit']) / fixed_result['total_profit'] * 100,(optimal_result['D_total'] - fixed_result['D_total']) / fixed_result['D_total'] * 100,(fixed_result['c'] - optimal_result['c']) / fixed_result['c'] * 100,(coordination_efficiency - fixed_result['total_profit'] / ideal_profit) * 100]}df_comparison = pd.DataFrame(comparison_data)st.dataframe(df_comparison.style.format({'Pre-Coordination': '{:,.2f}','Post-Coordination': '{:,.2f}','Improvement %': '{:+.2f}%'}), width='stretch')# 网络结构对协调效果的影响分析st.markdown("#### Network Structure Impact on Coordination")M_range = [2, 5, 10, 20]N_range = [2, 5, 10, 20]efficiency_data = []profit_data = []# 简化计算,避免长时间等待for m in M_range[:3]: # 只计算前3个值加快速度for n in N_range[:3]:temp_result, _ = model.find_optimal_contract(m, n)if temp_result:# 计算协调效率ideal_res = minimize(model.centralized_profit, [10000, 5000],bounds=[(0, None), (0, None)], method='L-BFGS-B')if ideal_res.success:ideal_profit = -ideal_res.funefficiency = temp_result['total_profit'] / ideal_profit if ideal_profit > 0 else 0efficiency_data.append({'M': m, 'N': n, 'Efficiency': efficiency})profit_data.append({'M': m, 'N': n, 'Profit': temp_result['total_profit'] / 10000})if efficiency_data and profit_data:# 协调效率热力图eff_df = pd.DataFrame(efficiency_data)pivot_eff = eff_df.pivot_table(values='Efficiency', index='M', columns='N')# 利润热力图profit_df = pd.DataFrame(profit_data)pivot_profit = profit_df.pivot_table(values='Profit', index='M', columns='N')fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))# 协调效率热力图sns.heatmap(pivot_eff, annot=True, fmt='.2%', cmap='YlOrRd', ax=ax1,cbar_kws={'label': 'Coordination Efficiency'})ax1.set_title('Supply Chain Coordination Efficiency by Network Structure')ax1.set_xlabel('Retailer Count (N)')ax1.set_ylabel('Supplier Count (M)')# 系统利润热力图sns.heatmap(pivot_profit, annot=True, fmt='.0f', cmap='YlGnBu', ax=ax2,cbar_kws={'label': 'System Profit (10k Yuan)'})ax2.set_title('Total System Profit by Network Structure')ax2.set_xlabel('Retailer Count (N)')ax2.set_ylabel('Supplier Count (M)')plt.tight_layout()st.pyplot(fig)st.caption("Note: Coordination Efficiency = Coordinated System Profit / Centralized Optimal Profit")else:st.error("Optimal contract search failed, please adjust model parameters")if __name__ == "__main__":main()
