[优选算法专题七.分治-快排 ——NO.42~44 颜色分类、排序数组、数组中的第K个最大元素]
一、颜色分类
题目链接
75. 颜色分类
题目描述
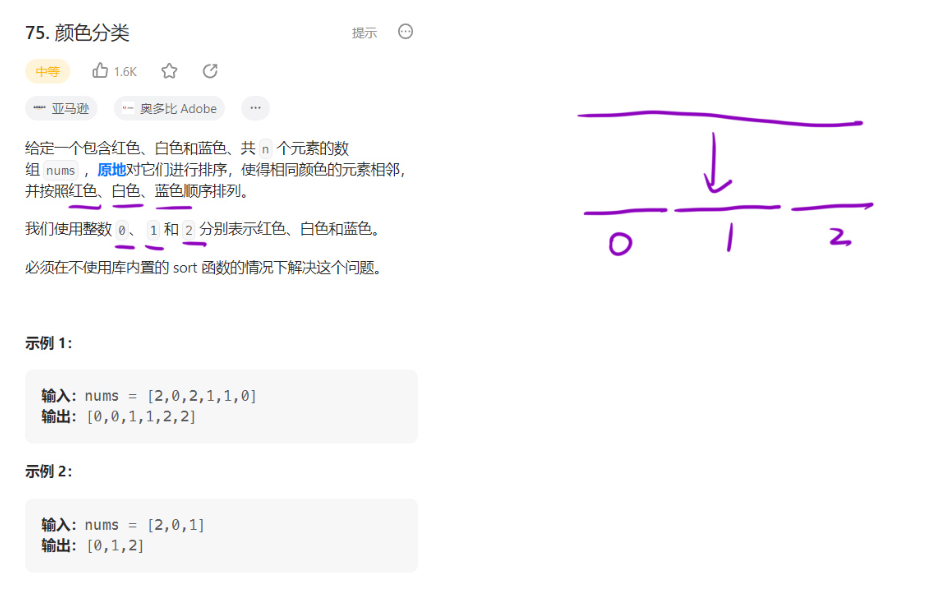
题目解析:
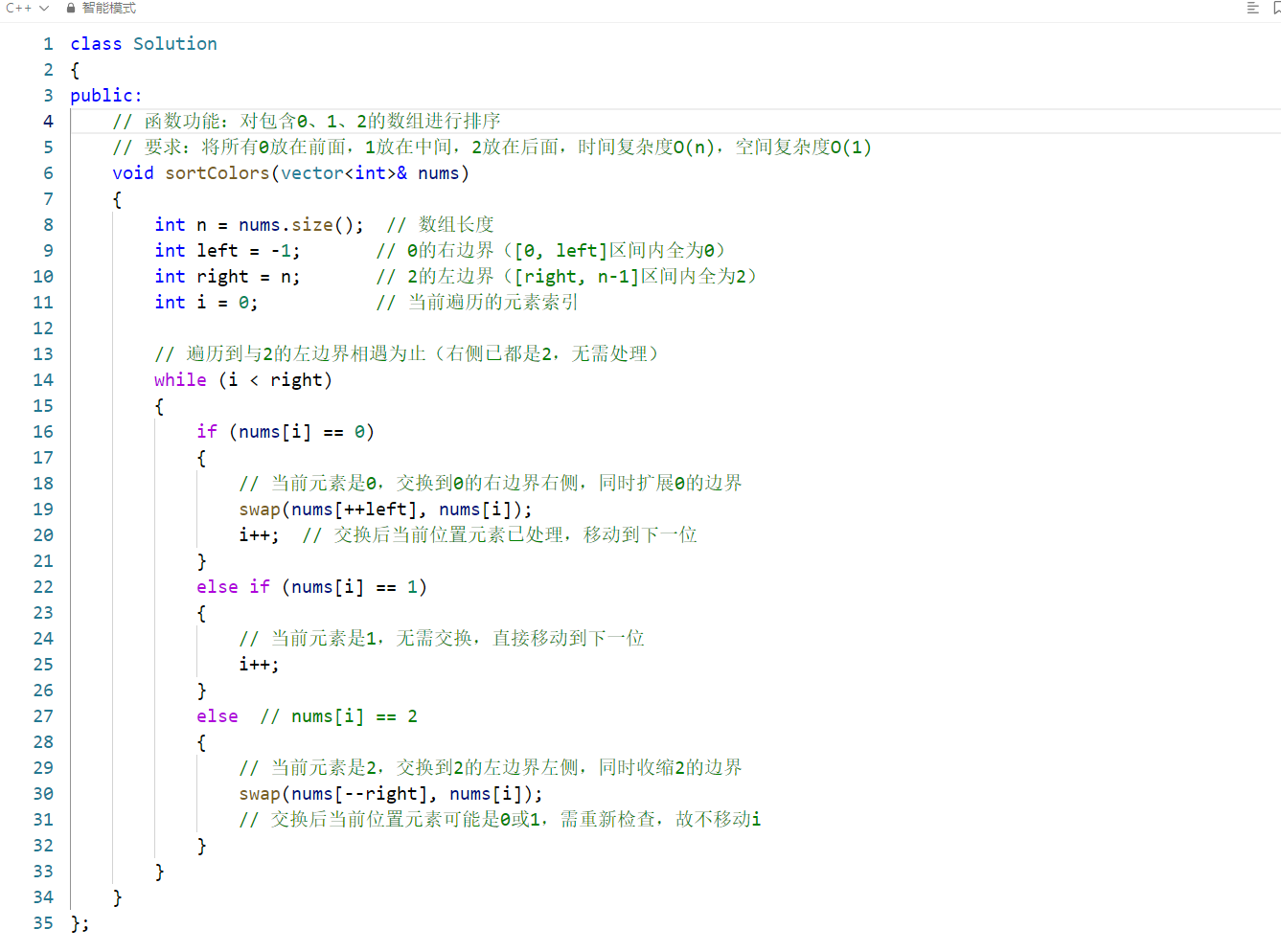
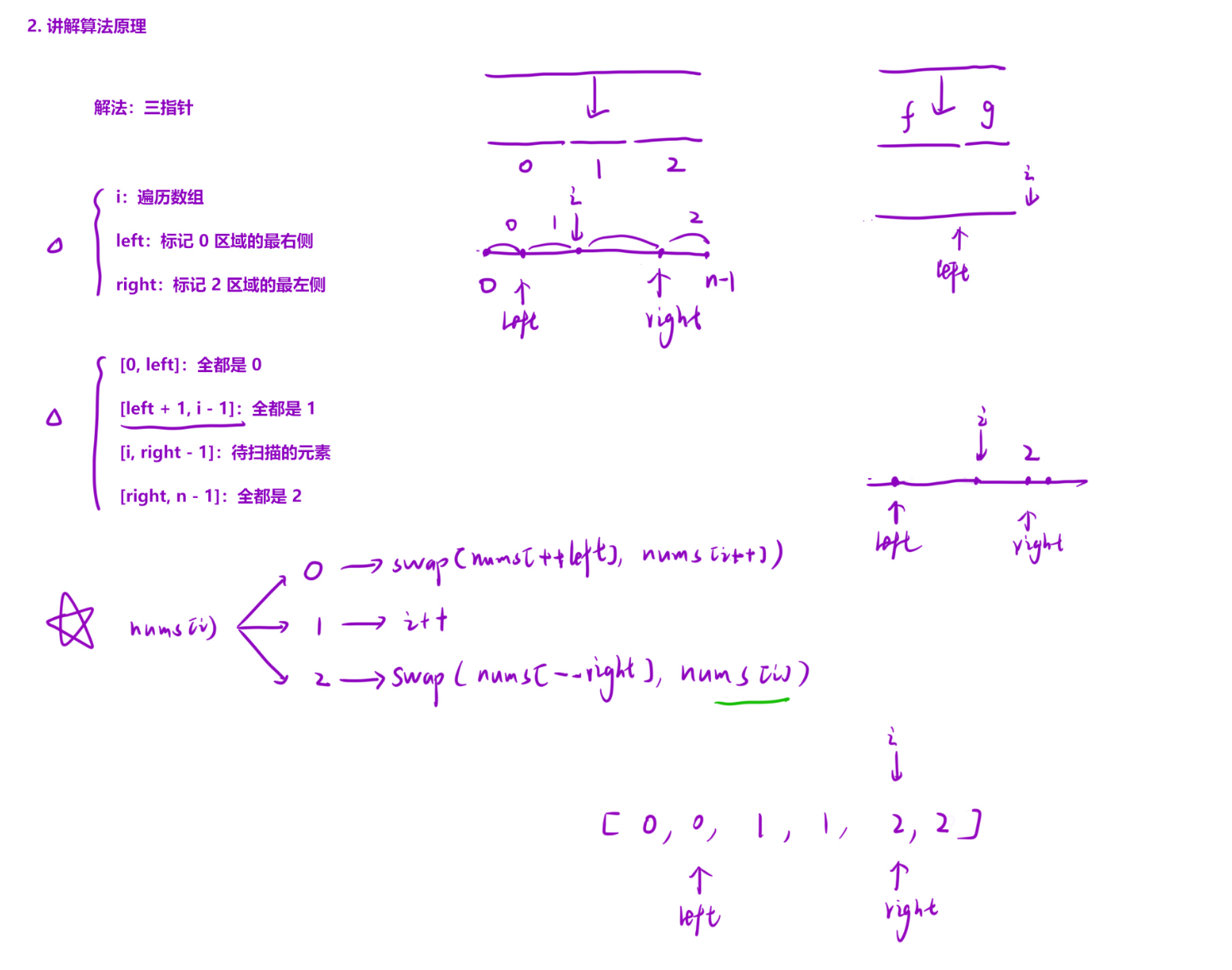
逻辑分析
-
边界定义:
left:标记 0 的右边界(初始为 - 1,意为暂无 0),[0, left]区间内全是 0。right:标记 2 的左边界(初始为 n,意为暂无 2),[right, n-1]区间内全是 2。i:当前遍历的元素索引,初始为 0,遍历范围是[left+1, right-1](未处理的中间区域)。
-
遍历规则:
- 若
nums[i] == 0:需要放到 0 的区域,将其与left+1位置的元素交换,同时left右移(扩展 0 的区域),i右移(当前元素已处理)。 - 若
nums[i] == 1:本身就在中间区域,无需交换,i直接右移。 - 若
nums[i] == 2:需要放到 2 的区域,将其与right-1位置的元素交换,同时right左移(收缩 2 的区域),i不移动(交换后当前位置元素可能是 0 或 1,需重新检查)。
- 若
-
终止条件:当
i >= right时,说明中间未处理区域已空,排序完成。
复杂度分析
- 时间复杂度:
O(n),每个元素最多被遍历一次(i和right移动总次数不超过 n)。 - 空间复杂度:
O(1),仅使用常数个额外变量,原地排序。
二、快速排序
题目链接
912. 排序数组
题目描述:
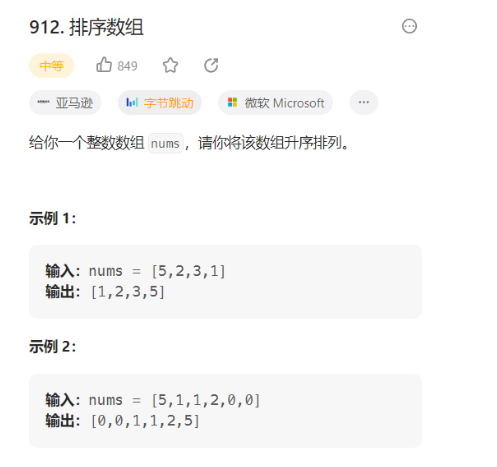

解析
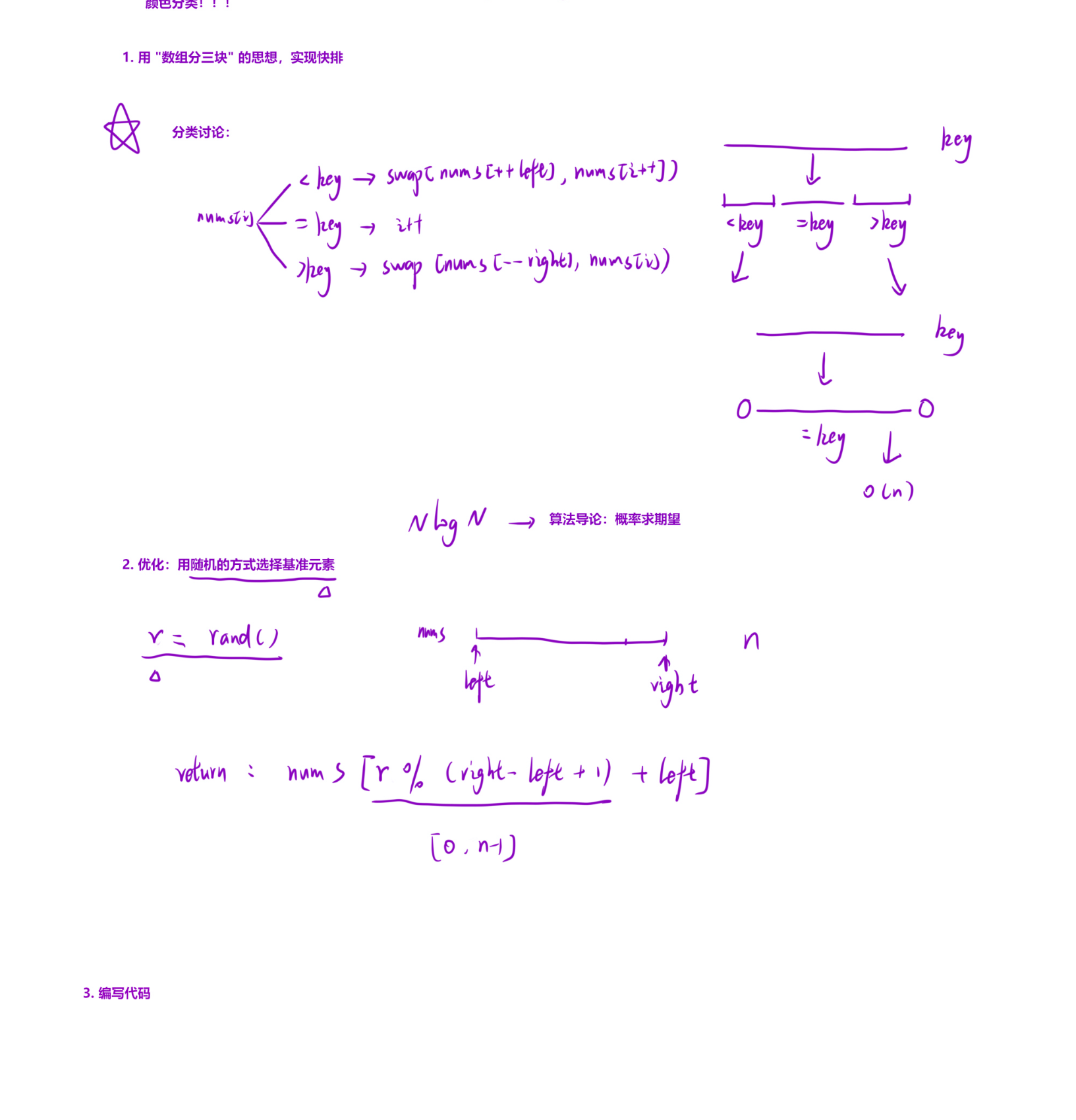
核心算法:快速排序(三向切分优化)
这是一个基于快速排序的数组排序实现,通过「三向切分」优化处理重复元素,同时引入随机选择基准值避免最坏情况,提高排序效率。
逻辑分析
-
快速排序核心思想:通过选择一个「基准值(key)」,将数组划分为三部分:小于 key 的元素、等于 key 的元素、大于 key 的元素。然后递归排序小于 key 和大于 key 的两部分,最终实现整体有序。
-
三向切分的优势:传统快速排序对重复元素较多的数组效率较低(可能导致不平衡划分)。三向切分将等于 key 的元素集中在中间,避免对这部分元素重复排序,大幅优化含大量重复元素的场景。
-
随机选择基准值:通过
getRandom函数在当前区间内随机选择基准值,避免因数组有序(或接近有序)导致的最坏情况(时间复杂度退化到O(n²)),期望时间复杂度稳定在O(n log n)。 -
递归流程:
- 若区间
[l..r]长度小于 2,直接返回(递归终止)。 - 随机选择基准值
key,通过三向切分将区间划分为[l..left](小于 key)、[left+1..right-1](等于 key)、[right..r](大于 key)。 - 递归排序
[l..left]和[right..r]。
- 若区间
复杂度分析
- 时间复杂度:期望
O(n log n),最坏O(n²)(但随机化后概率极低)。 - 空间复杂度:
O(log n)(递归调用栈的深度,平均为log n,最坏O(n))。
题目链接
215. 数组中的第K个最大元素
题目描述

题目解析

核心逻辑拆解
1. 算法核心思想
快速选择算法是快速排序的变种,无需完全排序数组:
- 每次通过 “分区” 将数组分成三部分(小于 / 等于 / 大于基准值)。
- 判断第 k 大元素在哪个分区,仅递归处理目标分区,大幅减少计算量。
2. 关键函数解析
(1)主函数 findKthLargest
- 初始化随机数种子,为后续随机选择基准值做准备(避免有序数组时分区失衡,导致时间复杂度退化到 O (n²))。
- 调用核心的快速选择函数
qsort,指定初始区间为整个数组(0 到 nums.size ()-1)。
(2)核心函数 qsort(快速选择逻辑)
- 递归终止条件:当区间缩小到只有一个元素(l==r),该元素就是目标(此时 k=1)。
- 步骤 1:随机选择基准值:通过
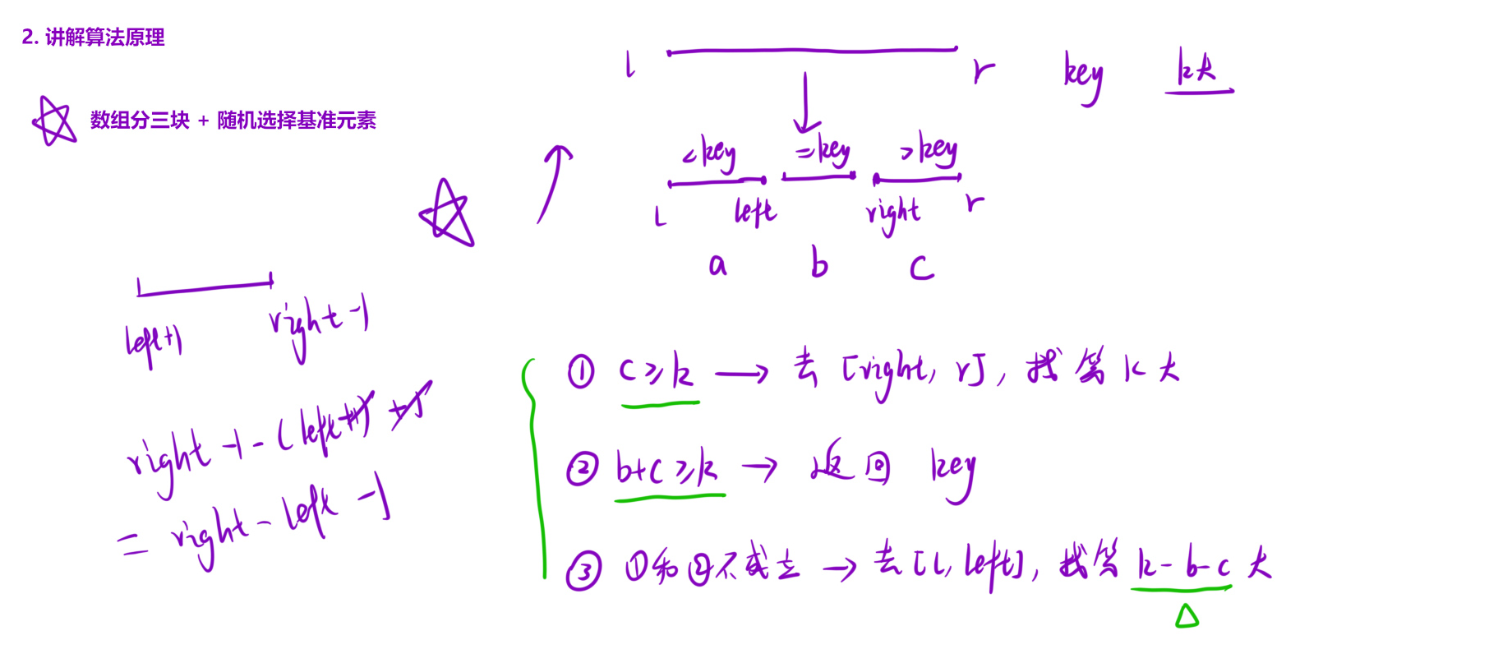
getRandom函数在当前区间随机选一个元素作为 key,保证分区的随机性。 - 步骤 2:三色分区:
- 用三个指针划分区间:[l, left](小于 key)、[left+1, right-1](等于 key)、[right, r](大于 key)。
- 遍历数组时,根据元素与 key 的大小关系,将元素交换到对应区域,避免重复处理相等元素(提升效率)。
- 步骤 3:定位目标分区:
- 计算 “大于 key 的元素个数 c” 和 “等于 key 的元素个数 b”。
- 若 c≥k:第 k 大在右侧(大于 key 的区域),递归处理 [right, r]。
- 若 b+c≥k:第 k 大在中间(等于 key 的区域),直接返回 key(无需继续递归)。
- 否则:第 k 大在左侧(小于 key 的区域),调整 k 为 k-b-c(减去右侧和中间区域的元素个数),递归处理 [l, left]。
(3)辅助函数 getRandom
- 生成 [left, right] 范围内的随机索引,返回对应元素作为基准值,确保分区的随机性。
3.时间与空间复杂度
- 时间复杂度:
- 平均情况:O (n)(每次分区排除一半元素,总操作次数为 n + n/2 + n/4 + ... ≈ 2n)。
- 最坏情况:O (n²)(极端随机下分区始终失衡,但实际概率极低)。
- 空间复杂度:O (log n)(递归调用栈的深度,平均为 log n)。
4.优势与注意事项
- 优势:
- 效率高:平均 O (n) 时间,适合大数据量场景。
- 原地操作:无需额外空间存储数组副本。
- 处理重复元素:三色分区直接跳过相等元素,避免无效交换。
- 注意事项:
- 必须初始化随机数种子(
srand(time(NULL))),否则可能退化到 O (n²)。 - 需确保 k 的有效性(1 ≤ k ≤ 数组长度),否则可能越界。
- 必须初始化随机数种子(
总结
该代码通过 “随机基准 + 三色分区 + 递归减治” 实现了高效的第 k 大元素查找,是面试中解决此类问题的最优方案之一。核心在于利用分区快速缩小查找范围,避免全量排序的冗余计算。
