从零开始学二叉树(上):树的初识 —— 从文件系统到树的基本概念
目录
🌱 引言:你每天都在用“树”,只是没意识到
1️⃣ 什么是树?—— 一种“非线性”的层次结构
线性 vs 非线性:从“排队”到“家族谱”
📌 树的正式定义(别怕,我们慢慢啃)
2️⃣ 树 vs 线性表 vs 图:三兄弟谁是谁?
3️⃣ 树的基本术语详解(生活化比喻)
🔹 父结点(Parent) / 子结点(Child)
🔹 兄弟结点(Sibling)
🔹 结点的度(Degree)
🔹 叶子结点(Leaf) vs 分支结点(Internal Node)
🔹 层次(Level) 与 高度(Height)
🔹 祖先(Ancestor) 与 子孙(Descendant)
🔹 路径(Path)
🔹 森林(Forest)
4️⃣ 树怎么在 C 语言里“存”下来?
❓ 思考:每个结点要存什么?
🌟 孩子兄弟表示法(Child-Sibling Representation)
✨ 举个转换例子:
5️⃣ 树的现实应用:不止是文件系统!
✅ 本篇小结 & 学习建议
💡 思考题(动手更深刻!)
💡 思考题(动手更深刻!)
📢 下期预告:《从零开始学二叉树(中):堆与完全二叉树的奥秘》
作者:一位踩过坑、画过遍历图、调错过指针的大二学生 东岸
目标读者:刚学完 C 语言、正在啃数据结构的大一/大二同学
一句话预告:这是一场从“文件夹”出发,通往“递归思维”的旅程。
🌱 引言:你每天都在用“树”,只是没意识到
想象一下:你打开电脑,双击“此电脑” → 进入“D盘” → 打开“学习资料” → 点进“数据结构作业” → 最终找到那个名为 tree.c 的文件。
这个路径:
D:\ → 学习资料 → 数据结构作业 → tree.c
是不是一层套一层?有没有一种“根在上、叶在下”的结构感?
没错!这正是树形结构在现实中最常见的应用——文件系统。
很多同学刚接触“树”这个概念时,总觉得抽象、玄乎,甚至害怕。其实你早就和它朝夕相处了,只是不知道它的名字罢了。今天,我们就从这个熟悉的“文件夹”出发,一起揭开“树”的神秘面纱。
1️⃣ 什么是树?—— 一种“非线性”的层次结构
线性 vs 非线性:从“排队”到“家族谱”
你学过数组、链表,它们是线性结构:数据一个接一个,像排队打饭,前后关系明确。
但现实世界很多东西不是排队,而是分层、分枝的。比如:
- 家谱:你 → 父母 → 祖父母 → 曾祖父母……
- 公司组织架构:CEO → 部门总监 → 小组长 → 员工
- HTML DOM 树:
<html>→<body>→<div>→<p>
这些结构有一个共同点:一个“上级”可以有多个“下级”,但每个“下级”只能有一个“上级”。这就是树!
📌 树的正式定义(别怕,我们慢慢啃)
树是由 n(n ≥ 0)个有限结点组成的具有层次关系的集合。它有一个特殊的根结点(root),其余结点被分成若干个互不相交的子树。
关键点来了:
- 递归定义:一棵树 = 根 + 若干棵子树。而每棵子树,本身也是一棵树!
→ 这就是树的“递归之美”,也是后续遍历、建树等操作的理论基础。 - 互不相交:子树之间不能共享结点,否则就不是树,而是图了(那是后话)。
- n 个结点 → n-1 条边:因为除了根,每个结点都只有一个爸爸(父结点)。
👉 举个栗子:
假设你有一个文件夹结构如下:
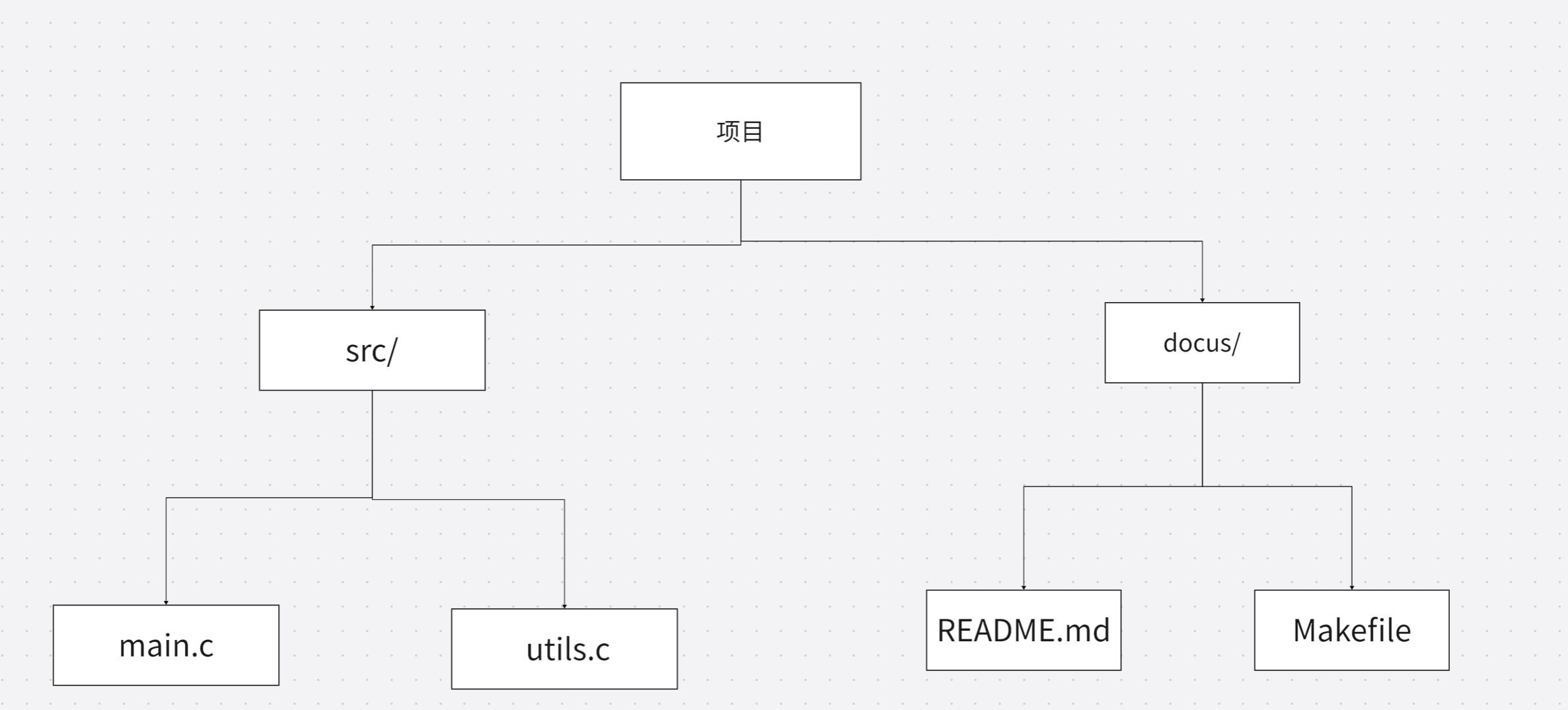
- 根结点是
项目/ src/和docs/是项目/的孩子结点main.c、utils.c是src/的孩子README.md是docs/的孩子Makefile是项目/的另一个孩子
整个结构就是一棵树!
2️⃣ 树 vs 线性表 vs 图:三兄弟谁是谁?
| 结构 | 特点 | 类比 | 适用场景 |
| 线性表 | 一对一,顺序访问 | 排队打饭 | 存储有序数据 |
| 树 | 一对多,层次分明 | 家族族谱、文件系统 | 表达层级关系 |
| 图 | 多对多,任意连接 | 社交网络(A认识B,B认识C,C又认识A) | 路径规划、关系网络 |
✅ 重点提醒:
树 ≠ 图!
树中任意两个结点之间只有唯一路径;而图可以有环、有多个路径。
所以——树是图的特例,但图不是树。
3️⃣ 树的基本术语详解(生活化比喻)
别被术语吓到!我们一个个来,配上例子,保你秒懂。
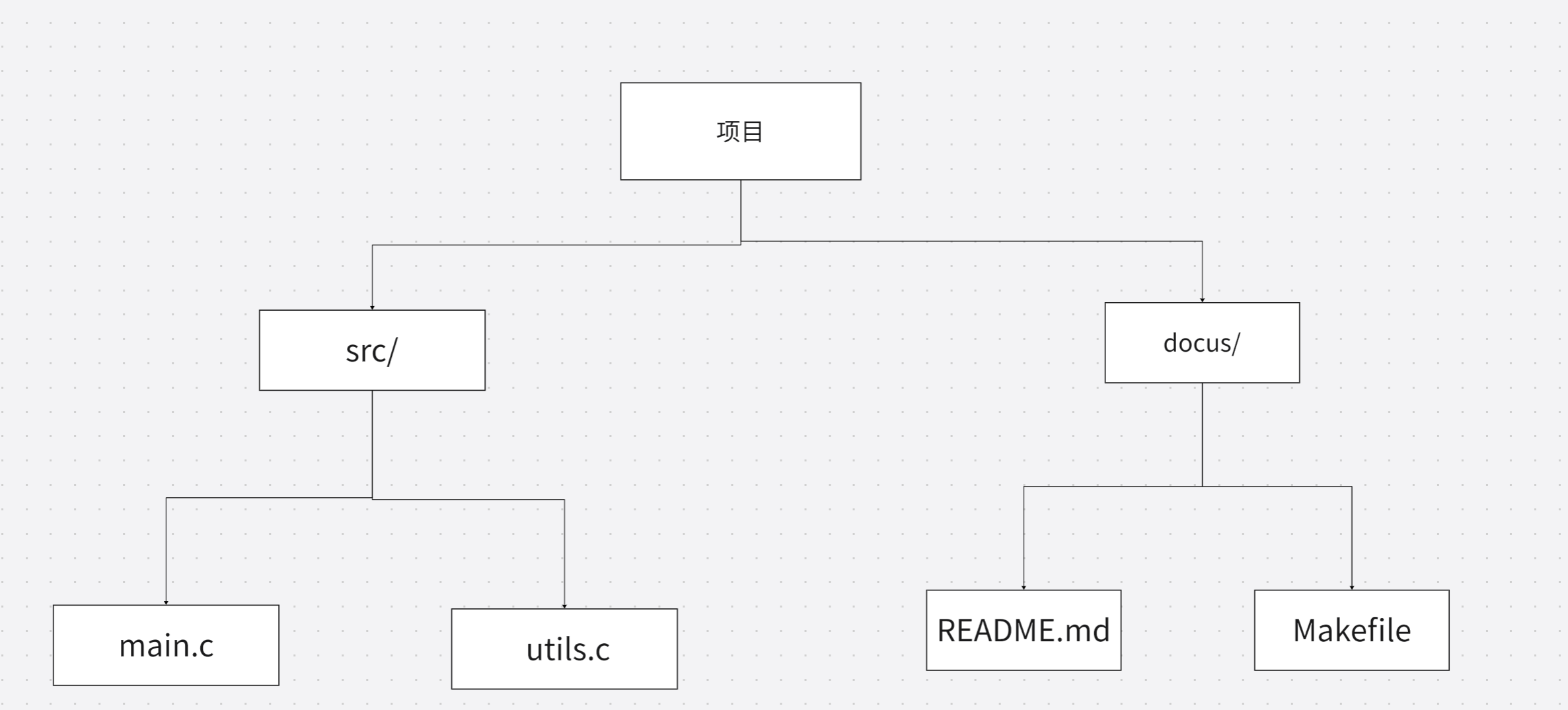
🔹 父结点(Parent) / 子结点(Child)
- 父结点:有孩子的结点
- 子结点:被某个结点“生出来”的结点
比如:你爸是你父结点,你是你爸的子结点(之一)。
在文件系统中,src/是main.c的父目录(即父结点)。
🔹 兄弟结点(Sibling)
有同一个爸爸的结点互为兄弟。
比如:main.c 和 utils.c 都是 src/ 的孩子 → 它们是亲兄弟!
🔹 结点的度(Degree)
一个结点有多少个孩子,它的“度”就是多少。
项目/有 3 个孩子(src/、docs/、Makefile)→ 度 = 3main.c没有孩子 → 度 = 0
📝 树的度 = 所有结点中最大的度。比如上面例子中树的度是 3。
🔹 叶子结点(Leaf) vs 分支结点(Internal Node)
- 叶子结点:度为 0 的结点 → 没有孩子的“终端”结点
→main.c、utils.c、README.md、Makefile都是叶子 - 分支结点:度 ≥ 1 的结点 → 有孩子的“中间”结点
→项目/、src/、docs/是分支结点
✅ 记忆技巧:叶子 = 最底层的文件;分支 = 中间的文件夹。
🔹 层次(Level) 与 高度(Height)
- 根在第 1 层
- 孩子在第 2 层,孙子在第 3 层……
- 树的高度 = 最大层数
上例中:
项目/:第 1 层src/、docs/、Makefile:第 2 层main.c等:第 3 层
→ 树的高度 = 3
🔹 祖先(Ancestor) 与 子孙(Descendant)
- 祖先:从根到该结点路径上的所有结点(包括根,不包括自己)
→main.c的祖先是:src/、项目/ - 子孙:以某结点为根的子树中的所有结点
→项目/的子孙是它下面所有文件和文件夹
🔹 路径(Path)
从结点 A 到结点 B,沿父子关系走的路线。
比如从 main.c 到 README.md 的路径是:
main.c ← src/ ← 项目/ → docs/ → README.md
(注意:必须经过共同祖先)
🔹 森林(Forest)
多棵树组成的集合。
比如你电脑里有:
D:\学习资料(一棵树)D:\游戏(另一棵树)
合起来就是森林。
💡 小知识:把森林中每棵树的根连到一个虚拟根上,就变成一棵大树。这在某些算法中有用!
4️⃣ 树怎么在 C 语言里“存”下来?
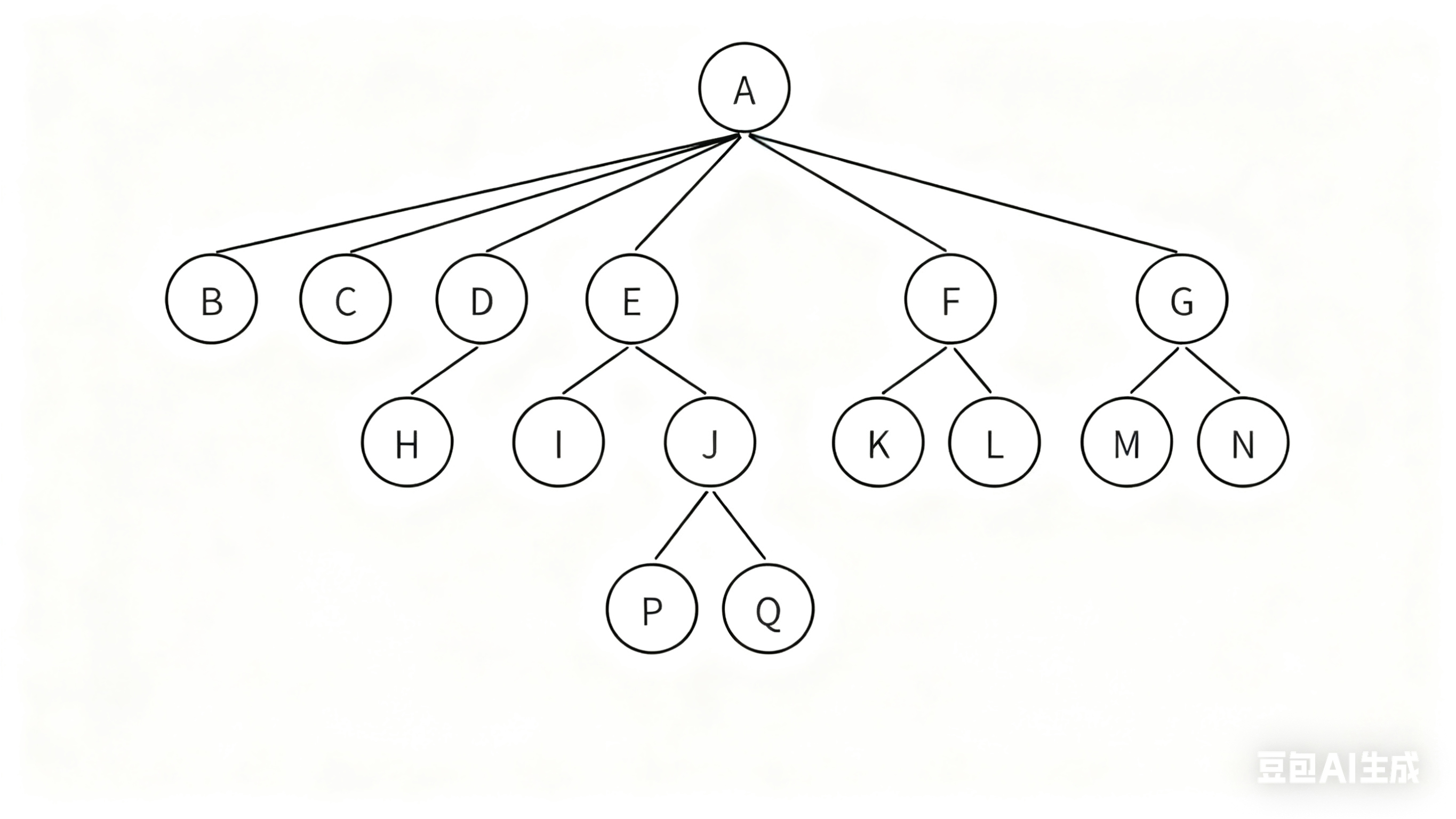
线性表可以用数组或链表,那树这么“分叉”的结构,怎么存?
❓ 思考:每个结点要存什么?
- 数据本身(比如文件名)
- 和孩子的联系(有几个孩子?分别是谁?)
但问题来了:每个结点的孩子数量不确定!有的 0 个,有的 6 个(就像 PDF 里的例子 A 有 6 个孩子)。
如果用“每个结点开 6 个指针”,那叶子结点就浪费了 6 个指针的空间。
于是,前辈们想出了一个聪明办法:
🌟 孩子兄弟表示法(Child-Sibling Representation)
核心思想:把“多叉树”转成“二叉树”来存!
每个结点只存两个指针:
child:指向第一个孩子brother:指向右边的下一个兄弟
struct TreeNode {int data; // 数据域(比如文件名哈希值)struct TreeNode* child; // 第一个孩子struct TreeNode* brother; // 右边的兄弟
};✨ 举个转换例子:
原始树:
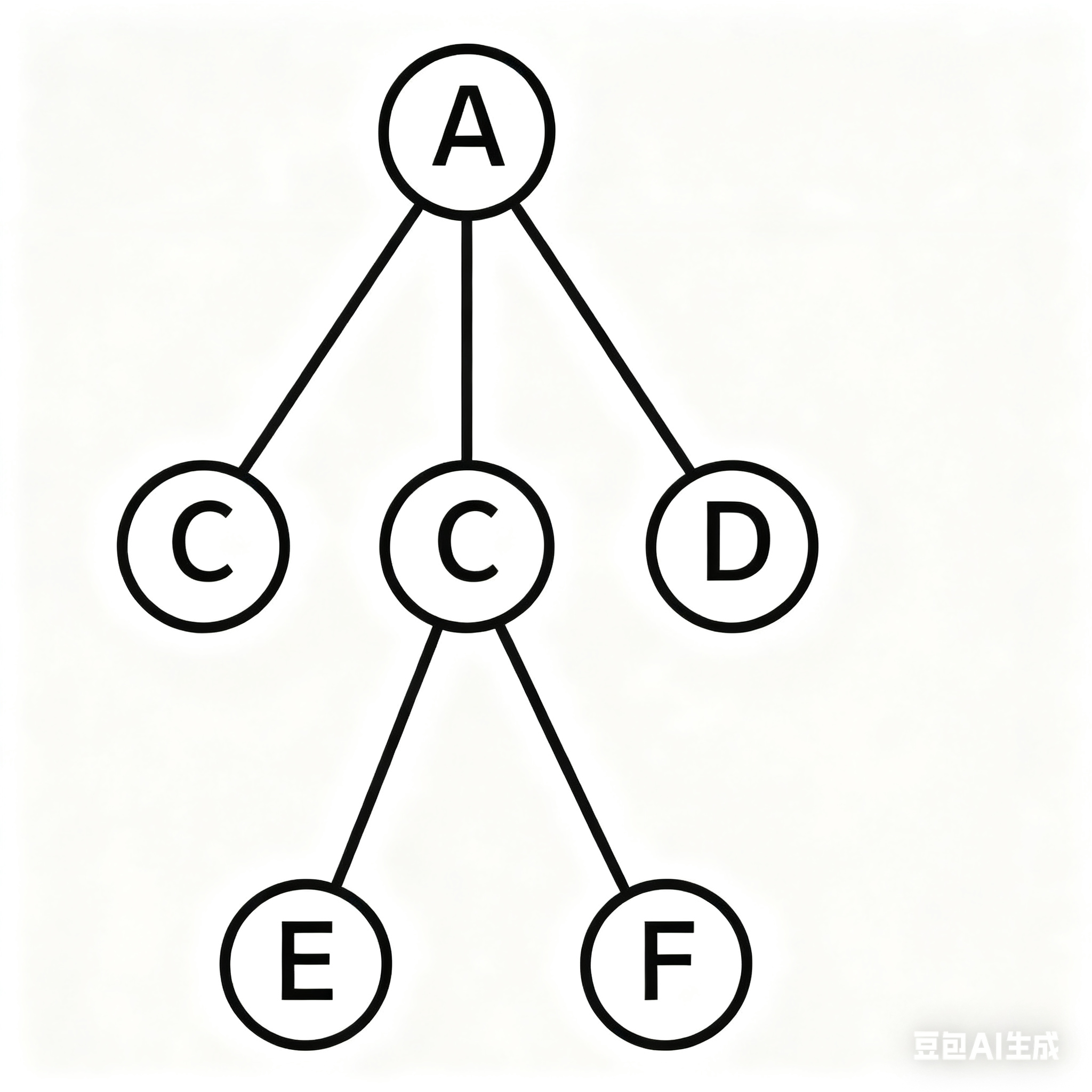
用孩子兄弟法变成:
A
|
B — C — D
|
E — F
- A 的
child= B;B 的brother= C;C 的brother= D - C 的
child= E;E 的brother= F
✅ 优点:
- 每个结点固定两个指针,节省空间
- 天然转化为二叉树,后续所有二叉树算法都能用!
📌 这就是为什么我们重点学“二叉树” —— 它是树结构的“通用表示法”!
5️⃣ 树的现实应用:不止是文件系统!
虽然文件系统是最直观的例子,但树的应用远不止于此:
| XML / JSON 解析 | 层级嵌套天然对应树结构 |
| 编译器语法树(AST) | 把代码解析成语法树,便于分析和优化 |
| 数据库索引(B+树) | 快速查找、范围查询的底层结构 |
| 决策树(机器学习) | 通过树形规则做分类预测 |
| 红黑树(C++ map/set) | 保证插入、查找 O(log n) 的平衡树 |
🔍 踩坑经历:
我第一次写编译器实验,看到“抽象语法树”四个字直接懵了。
后来画了张图,发现就是“if-else”套“for”套“表达式”——不就是树嘛!
画图,是理解树结构最有效的武器!
✅ 本篇小结 & 学习建议
| 树是递归结构 | 根 + 子树,子树也是树 |
| 非线性 = 分层分叉 | 不像数组那样“一条线” |
| 术语要结合例子记 | 别死背定义,用文件夹类比 |
| 孩子兄弟法很妙 | 把多叉转二叉,统一处理 |
| 树无处不在 | 从文件系统到 AI,都在用 |
💡 思考题(动手更深刻!)
- 画一画:在纸上画出你
C:\Users\你的名字目录下的三层结构,标出根、叶子、兄弟。 - 想一想:为什么说“树中任意两结点间有且仅有一条路径”?如果出现两条路径,会发生什么?
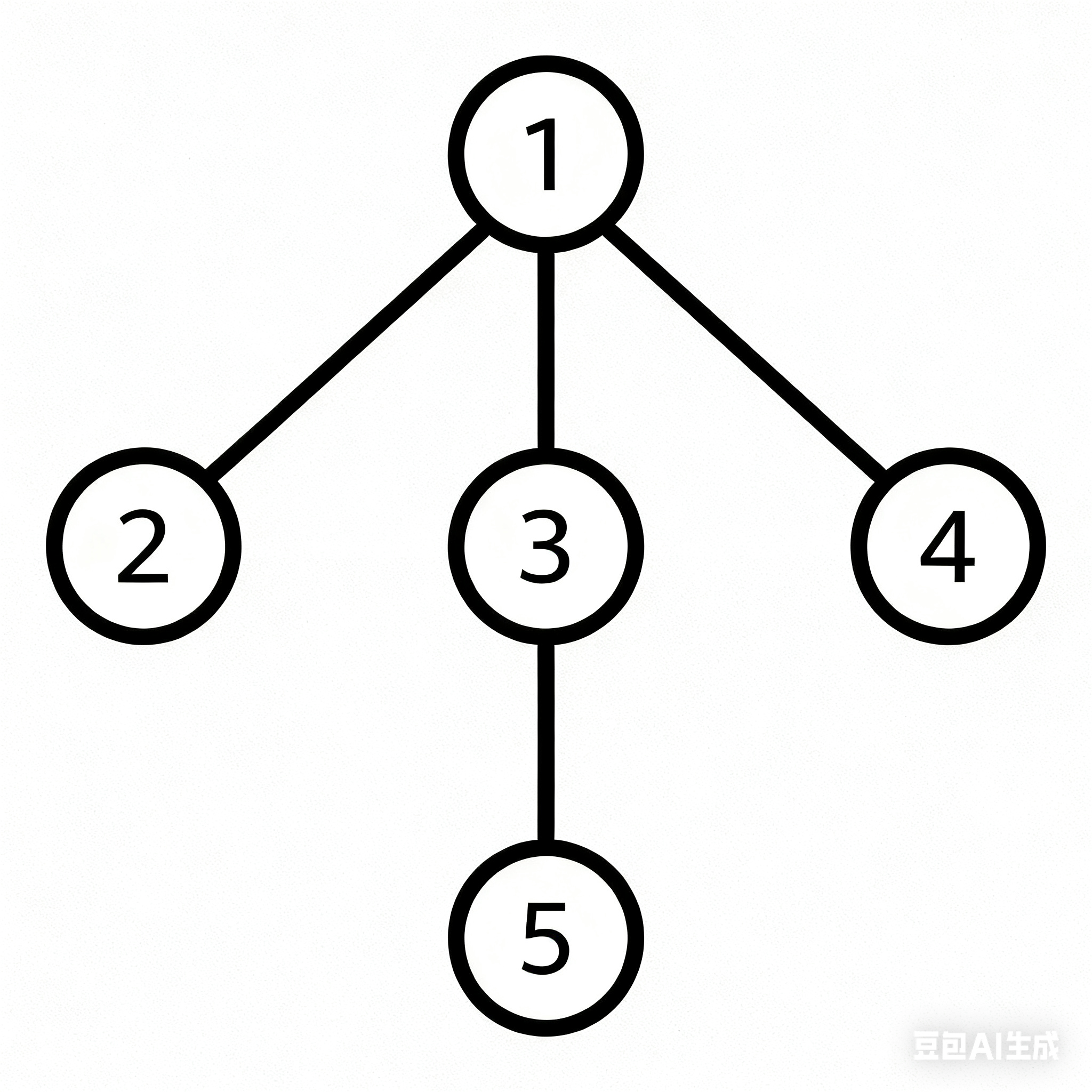
- 试一试:用孩子兄弟表示法,手动将下面这棵树转为二叉形式
💡 思考题(动手更深刻!)
- 画一画:在纸上画出你
C:\Users\你的名字目录下的三层结构,标出根、叶子、兄弟。 - 想一想:为什么说“树中任意两结点间有且仅有一条路径”?如果出现两条路径,会发生什么?
- 试一试:用孩子兄弟表示法,手动将下面这棵树转为二叉形式
📢 下期预告:《从零开始学二叉树(中):堆与完全二叉树的奥秘》
我们将深入:
- 为什么完全二叉树能用数组高效存储?
- 堆到底是啥?为什么插入/删除只要 O(log n)?
- Top-K 问题:如何用一个小堆在百万数据中秒找前 10 名?
更有向上调整 vs 向下调整的复杂度对决,带你理解为什么“建堆用向下调整更快”!
🌟 寄语:
数据结构不是魔法,而是对现实世界的建模。
你不是在学“树”,你是在学如何用代码表达层次与关系。
下次看到文件夹,别只想着找作业——想想它的“树形灵魂”吧!
欢迎在评论区留言你的思考题答案,或分享你生活中的“树结构”例子!
👉 点赞 + 收藏 + 关注,不迷路!
感谢,各位同学的观看


