【多源 BFS】3.地图中的最⾼点（medium）

3.地图中的最⾼点（medium）

题⽬链接：1765. 地图中的最⾼点

题⽬描述：

给你⼀个⼤⼩为 m x n 的整数矩阵 isWater ，它代表了⼀个由 陆地 和 ⽔域 单元格组成的地
图。
• 如果 isWater[i][j] = = 0 ，格⼦ (i, j) 是⼀个 陆地 格⼦。
• 如果 isWater[i][j] = = 1 ，格⼦ (i, j) 是⼀个 ⽔域 格⼦。
你需要按照如下规则给每个单元格安排⾼度：
• 每个格⼦的⾼度都必须是⾮负的。
• 如果⼀个格⼦是 ⽔域 ，那么它的⾼度必须为 0 。
• 任意相邻的格⼦⾼度差 ⾄多 为 1 。当两个格⼦在正东、南、西、北⽅向上相互紧挨着，就称它们为相邻的格⼦。（也就是说它们有⼀条公共边）
找到⼀种安排⾼度的⽅案，使得矩阵中的最⾼⾼度值 最⼤ 。
请你返回⼀个⼤⼩为 m x n 的整数矩阵 height ，其中 height[i][j] 是格⼦ (i, j) 的⾼度。如果有多种解法，请返回 任意⼀个 。
⽰例 1：

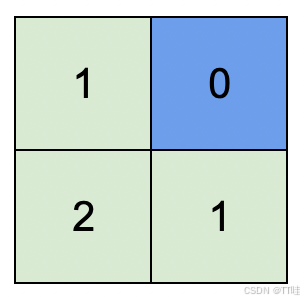
输⼊：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展⽰了给各个格⼦安排的⾼度。
蓝⾊格⼦是⽔域格，绿⾊格⼦是陆地格。
⽰例 2：

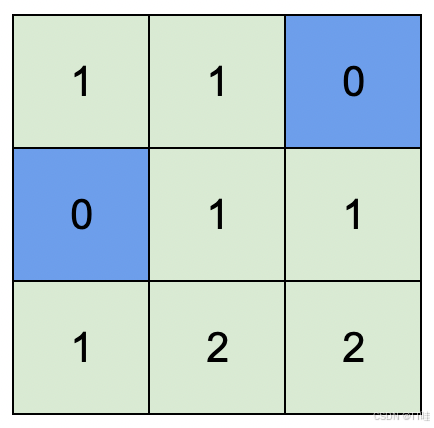
输⼊：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排⽅案中，最⾼可⾏⾼度为 2 。
任意安排⽅案中，只要最⾼⾼度为 2 且符合上述规则的，都为可⾏⽅案。
提⽰：
◦ m = = isWater.length
◦ n = = isWater[i].length
◦ 1 <= m, n <= 1000
◦ isWater[i][j] 要么是 0 ，要么是 1 。
◦ ⾄少有 1 个⽔域格⼦。

解法：

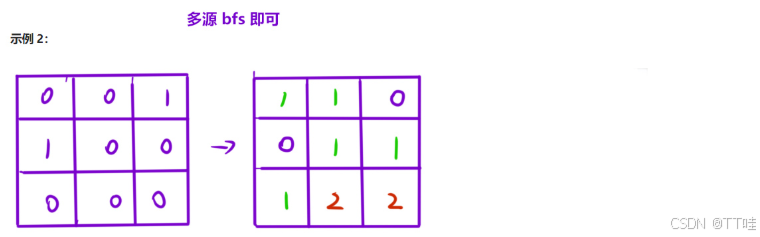
算法思路：

01矩阵的变型题，直接⽤多源 bfs 解决即可。

算法代码：

class Solution
{int[] dx = {0, 0, -1, 1};int[] dy = {1, -1, 0, 0};public int[][] highestPeak(int[][] isWater) {int m = isWater.length, n = isWater[0].length;int[][] dist = new int[m][n];for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)dist[i][j] = -1;Queue<int[]> q = new LinkedList<>();// 1. 所有的源点加⼊到队列⾥⾯for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(isWater[i][j] == 1){q.add(new int[]{i, j});dist[i][j] = 0;}// 2. 多源 bfswhile(!q.isEmpty()){int[] t = q.poll();int a = t[0], b = t[1];for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.add(new int[]{x, y});}}}return dist;}
}