当前位置：首页 > news >正文

超参数调优：Grid Search 和 Random Search 的实战对比

news 2025/11/15 13:27:20

模型训练完能够到达85%的准确率，很多人觉得就差不多了。但是通过超参数优化能让模型释放真正的潜力。最后那3-5个点的提升，往往决定了你的模型是"还行"还是"能打"。

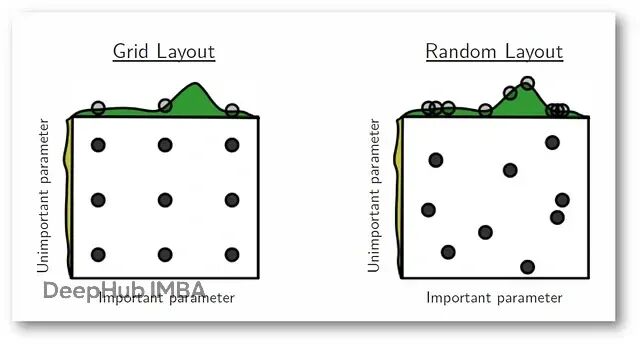
这篇文章会把Grid Search和Random Search这两种最常用的超参数优化方法进行详细的解释。从理论到数学推导，从优缺点到实际场景，再用真实数据集跑一遍看效果。

参数和超参数：两个容易混淆的概念

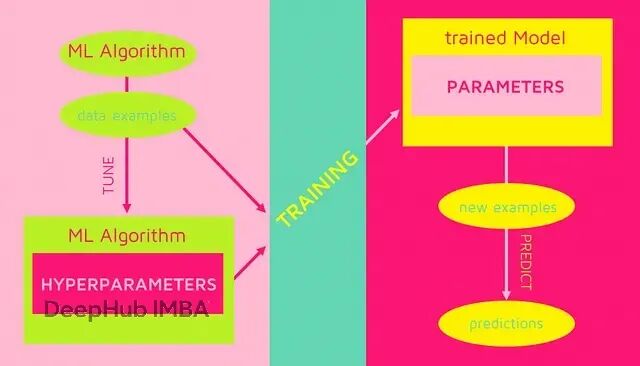
机器学习里，参数和超参数是完全不同的东西。

参数是模型自己从数据里学出来的。线性回归的权重系数w和偏置b，神经网络各层之间的连接权重，逻辑回归的决策边界系数，都属于参数。训练过程中这些值会不断调整，你不用手动去设。

超参数则不同，需要在训练开始前就定好。它们控制着模型怎么学习，学习能力有多强，正则化力度多大。

随机森林的n_estimators（树的数量）、max_depth（树能长多深）、min_samples_split（分裂需要的最少样本）都是超参数。神经网络的learning_rate（学习率）、batch_size（批次大小）、隐藏层数量也是。SVM里的C（正则化参数）、kernel（核函数）、gamma（核系数）也都是一些常见的超参数。

超参数优化的核心目标是在过拟合和欠拟合之间找平衡。只有找到最佳配置模型的泛化能力才能最大化，遇到新数据才能给出靠谱的预测。

已经有很多研究表明，超参数的选择对模型性能的影响不亚于参数优化本身。所以说系统性地调优超参数是构建可靠机器学习模型的必经之路。

Grid Search：最暴力也最稳妥的方法

Grid Search是超参数优化里最直接的思路：把所有组合都试一遍。

算法会扫描所有超参数值的笛卡尔积。你给每个超参数设定几个候选值，然后把这些值的所有可能组合都跑一遍，最后挑出表现最好的那组。

具体步骤很简单：

先定义参数空间，给每个超参数列出候选值
计算笛卡尔积，生成所有可能的组合
用交叉验证评估每个组合的性能
选出验证分数最高的那组参数

Grid Search最大的优点是能保证在离散参数空间里找到全局最优解，但代价也很明显：计算量爆炸。

总评估次数的增长是指数级的，如果有d个参数，每个参数n个候选值，就要评估 n^d 次。参数空间一大这个方法基本就跑不动了。

但是他的优势在于结果可复现，相同的参数空间和随机种子能得到一样的结果。搜索也很全面定义的空间里绝对能找到最优解。而且每个组合可以独立评估，适合并行计算。

劣势就是维度灾难，高维空间里计算成本根本承受不了。连续参数只能离散化处理，存在次优化问题。对那些不重要的参数也要遍历，白白浪费资源。

 print("--- EXPERIMENT 1: GridSearchCV (Small Space) Starting ---")
param_grid_small = {'C': [0.1, 1, 10, 100],'gamma': [1, 0.1, 0.01, 0.001],'kernel': ['rbf', 'poly']
}svc = SVC(random_state=42)
grid_search = GridSearchCV(estimator=svc,param_grid=param_grid_small,cv=5,scoring='accuracy',n_jobs=-1,verbose=0
)start_time_grid = time.time()
grid_search.fit(X_train_scaled, y_train)
end_time_grid = time.time()total_time_grid = end_time_grid - start_time_grid
grid_best_score = grid_search.best_score_print(f"GridSearch (Small) Finished. Time: {total_time_grid:.2f}s, Score: {grid_best_score:.4f}")

低维参数空间、计算资源充足的情况下Grid Search是个不错的选择，但高维问题就得考虑别的办法了。

Random Search：用概率换效率

Bergstra和Bengio在2012年提出Random Search，用概率方法解决Grid Search的计算瓶颈。

Random Search不再系统遍历而是从参数空间随机采样。给每个超参数定义概率分布，然后随机抽取若干组合进行评估。

操作流程：

为每个超参数指定概率分布
根据n_iter参数决定采样次数，随机生成参数组合
用交叉验证评估每组参数的性能
选出验证分数最高的配置

大多数机器学习模型里，真正影响性能的往往只有少数几个关键参数，其他参数的影响很边缘。Random Search正是利用了这个特点。

数学上可以这样理解：假设参数空间是d维的，最优区域在某个d维子空间里。那么Random Search找到最优区域的概率是：

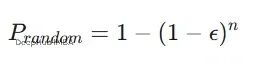
epsilon是最优区域的体积占比，n是采样次数。

好处是相同计算预算下能探索更广的参数空间。连续和离散参数都能处理，在高维问题上也适用。

缺点就是结果带有随机性，不能保证找到全局最优。而且分布的选择会影响结果，在有限次迭代内不保证收敛。

代码实现

 print("--- EXPERIMENT 2: RandomizedSearchCV (Small Space) Starting ---")
param_dist_small = {'C': loguniform(0.1, 100),'gamma': loguniform(0.001, 1),'kernel': ['rbf', 'poly']
}
N_ITERATIONS = 20svc = SVC(random_state=42)
random_search = RandomizedSearchCV(estimator=svc,param_distributions=param_dist_small,n_iter=N_ITERATIONS,cv=5,scoring='accuracy',n_jobs=-1,random_state=42,verbose=0
)start_time_random = time.time()
random_search.fit(X_train_scaled, y_train)
end_time_random = time.time()total_time_random = end_time_random - start_time_random
random_best_score = random_search.best_score_print(f"RandomSearch (Small) Finished. Time: {total_time_random:.2f}s, Score: {random_best_score:.4f}")

大参数空间实验

小规模实验看不出太大差别，所以我们换个更大更复杂的参数空间试试。这次加入poly核的额外参数degree和coef0。

这个实验会让Grid Search的维度诅咒问题暴露无遗。同时看看Random Search能不能在固定预算下高效找到好结果。

 print("--- EXPERIMENT 3: GridSearchCV (LARGE & Inefficient Space) Starting ---")
param_grid_large = {'C': [0.1, 1, 10, 100],'gamma': [1, 0.1, 0.01, 0.001],'kernel': ['rbf', 'poly'],'degree': [2, 3, 4],'coef0': [0.0, 0.5, 1.0]
}TOTAL_GRID_COMBINATIONS = 4 * 4 * 2 * 3 * 3
print(f"GridSearch (Large) Total Combinations: {TOTAL_GRID_COMBINATIONS}")
print(f"GridSearch (Large) Total Model Fits: {TOTAL_GRID_COMBINATIONS * 5}")svc = SVC(random_state=42)
grid_search_large = GridSearchCV(estimator=svc,param_grid=param_grid_large,cv=5,scoring='accuracy',n_jobs=-1,verbose=1
)start_time_grid_large = time.time()
grid_search_large.fit(X_train_scaled, y_train)
end_time_grid_large = time.time()total_time_grid_large = end_time_grid_large - start_time_grid_large
grid_large_best_score = grid_search_large.best_score_
grid_large_best_params = grid_search_large.best_params_print(f"\nGridSearch (Large) Finished.")
print(f"Total Time: {total_time_grid_large:.2f} seconds")print(f"Best CV Score: {grid_large_best_score:.4f}")

 print("--- EXPERIMENT 4: RandomizedSearchCV (LARGE Space) Starting ---")
param_dist_large = {'C': loguniform(0.1, 100),'gamma': loguniform(0.001, 1),'kernel': ['rbf', 'poly'],'degree': randint(2, 5),'coef0': uniform(0.0, 1.0)
}
N_ITERATIONS_LARGE = 30print(f"RandomSearch (Large) Budget: {N_ITERATIONS_LARGE}")
print(f"RandomSearch (Large) Total Model Fits: {N_ITERATIONS_LARGE * 5}")svc = SVC(random_state=42)
random_search_large = RandomizedSearchCV(estimator=svc,param_distributions=param_dist_large,n_iter=N_ITERATIONS_LARGE,cv=5,scoring='accuracy',n_jobs=-1,random_state=42,verbose=1
)start_time_random_large = time.time()
random_search_large.fit(X_train_scaled, y_train)
end_time_random_large = time.time()total_time_random_large = end_time_random_large - start_time_random_large
random_large_best_score = random_search_large.best_score_
random_large_best_params = random_search_large.best_params_print(f"\nRandomSearch (Large) Finished.")
print(f"Total Time: {total_time_random_large:.2f} seconds")print(f"Best CV Score: {random_large_best_score:.4f}")

结果对比

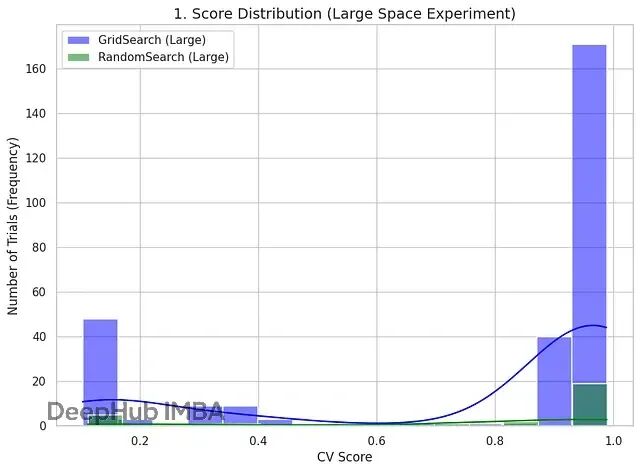
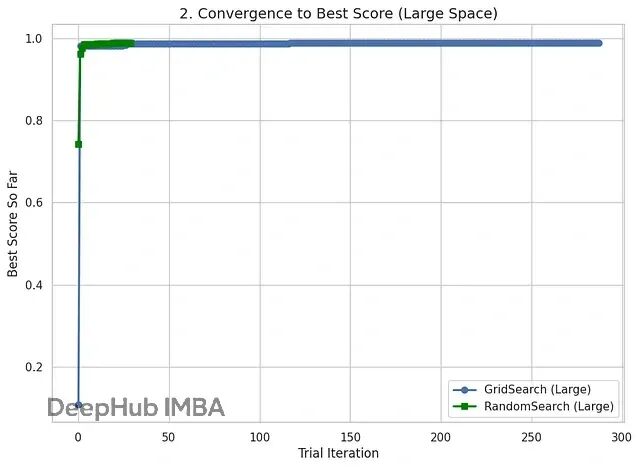
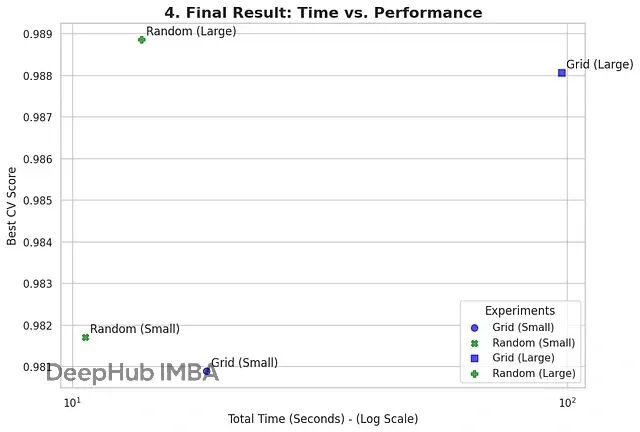
现在把小参数空间和大参数空间的实验结果放一起看：最佳CV分数（模型性能）和总耗时（计算效率）。

这个对比能清楚展示出，随着问题复杂度上升，两种优化策略各自的优势和性能成本权衡。

混合策略：取两者之长

前面的实验已经看到了Grid Search计算成本太高而Random Search扫描范围广但找精确最优点有点靠运气。

那能不能把两种方法的优势结合起来？

业界常用的Coarse-to-Fine策略就是这么干的：

第一阶段用Random Search快速扫描整个大参数空间，找到最有潜力的区域。

第二阶段在这个小区域周围跑密集的Grid Search，精确定位最优点。

这样既避免了全局Grid Search的天文计算量，又能得到高精度的调优结果。不用等几个星期就能拿到好结果。

现在拿实验4（大规模Random Search）找到的最佳参数作为起点，跑一遍混合策略看效果。

 print("--- EXPERIMENT 5: Hybrid 'Coarse-to-Fine' Strategy Starting ---")# 1. Get the best parameters from our 'Coarse' RandomSearch (Exp 4)
coarse_params = random_large_best_params
print(f"Coarse (RandomSearch) Best Params: {coarse_params}")best_C = coarse_params['C']
best_gamma = coarse_params['gamma']
best_kernel = coarse_params['kernel']# 2. Define a new, very TIGHT grid around these best parameters
# We will create 3 values around the best value (e.g., 0.8*best, best, 1.2*best)
# We use np.linspace to create a small range.
refined_param_grid = {'C': np.linspace(best_C * 0.8, best_C * 1.2, 3),'gamma': np.linspace(best_gamma * 0.8, best_gamma * 1.2, 3),'kernel': [best_kernel] # We already found the best kernel, no need to search again
}# Add kernel-specific params ONLY if they were found
if best_kernel == 'poly':best_degree = coarse_params['degree']best_coef0 = coarse_params['coef0']refined_param_grid['degree'] = [best_degree - 1, best_degree, best_degree + 1]refined_param_grid['coef0'] = np.linspace(best_coef0 * 0.8, best_coef0 * 1.2, 3)# Calculate combinations: 3 * 3 * 1 = 9 (or 3*3*1*3*3 = 81 if poly)
# This is still incredibly small compared to the 288 of the full GridSearch!# 3. Run the final 'Fine-Tuning' GridSearch
svc = SVC(random_state=42)
final_search = GridSearchCV(estimator=svc,param_grid=refined_param_grid,cv=5,scoring='accuracy',n_jobs=-1,verbose=1
)start_time_final = time.time()
final_search.fit(X_train_scaled, y_train)
end_time_final = time.time()total_time_final = end_time_final - start_time_final
final_best_score = final_search.best_score_print(f"\nHybrid 'Fine-Tuning' Search Finished.")
print(f"Total Time: {total_time_final:.2f} seconds")
print(f"Best CV Score (Hybrid): {final_best_score:.4f}")
print(f"Best Params (Hybrid): {final_search.best_params_}")# Create a new row for our final table
hybrid_experiment = {'Method': 'Hybrid (Random+Grid)','Combinations/Budget': f"{N_ITERATIONS_LARGE} (Random) + {len(final_search.cv_results_['params'])} (Grid)",'Total Model Fits (CV=5)': (N_ITERATIONS_LARGE * 5) + (len(final_search.cv_results_['params']) * 5),'Best Score': final_best_score,'Total Time (s)': total_time_random_large + total_time_final # Total time is BOTH steps
}# Add this to the existing DataFrame
final_df.loc['Experiment 5 (Hybrid)'] = hybrid_experiment
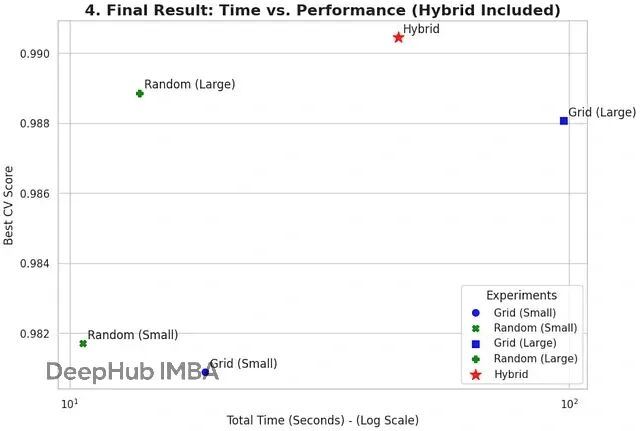
final_df = final_df.round(4)print("--- 🚀 FINAL COMPARISON (Hybrid Included) ---")display(final_df)