磁共振成像原理（理论）30：基本自旋回波成像 (Basic Spin-Echo Imaging)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 7.4

饱和恢复自旋回波序列

在磁共振成像中，普通的饱和恢复和反转恢复序列产生的是T1加权的自由感应衰减信号。然而，为了实现k空间的对称覆盖，通常采用回波信号进行数据采集。本节将详细讨论将自旋回波技术引入这些成像序列后所产生的图像对比度特性。

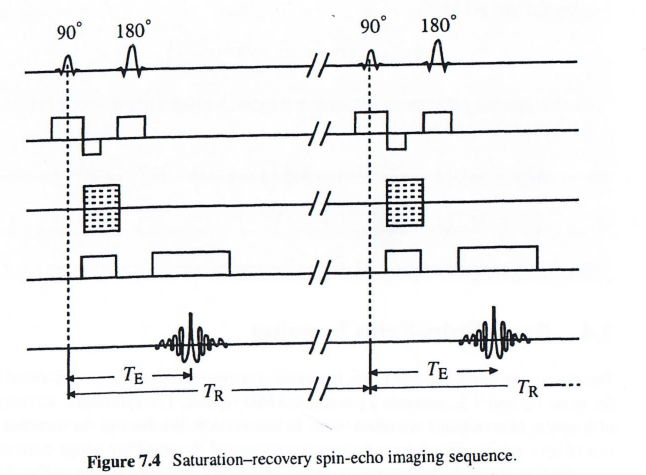
上图展示了饱和恢复自旋回波序列的时序图。该序列结合了饱和恢复的磁化准备机制和自旋回波的信号采集方式。

第1次饱和恢复：$0\le t<T_R$

在$t=0_{-}$时刻，即施加90°射频脉冲 (假设是$x^{\prime }$方向的)前，系统处于热平衡状态，纵向和横向磁化强度分别是：
$$\begin{array}{rl}{M}_z^{\prime }(0_{-})& =M_z^0\\ M_{x^{\prime }{y}^{\prime }}(0_{-})& =0\end{array}\text{\hspace{1em}()}$$

在$t=0_{+}$时刻，即施加90°射频脉冲后，纵向和横向磁化强度分别为：
$$\begin{array}{rl}{M}_z^{\prime }(0_{+})& =0\\ M_{x^{\prime }{y}^{\prime }}(0_{+})& =M_z^0\end{array}\text{\hspace{1em}()}$$

根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

在$0\le t<T_I$ 时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}(t)& =M_z^0\left(1-e^{-t/T_1}\right)& (0<t<T_I)\\ M_{x^{\prime }{y}^{\prime }}(t)& =M_z^0{e}^{-t/T_2}& (0<t<T_I)\end{array}\text{\hspace{1em}()}$$

在$t=T_{I-}$时刻，即180°脉冲施加前，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}(T_{I-})& =M_z^0\left(1-e^{-T_I/T_1}\right)& \\ M_{x^{\prime }{y}^{\prime }}(T_{I-})& =M_z^0{e}^{-T_I/T_2}& \end{array}\text{\hspace{1em}()}$$

理想180°射频脉冲给横向和纵向磁化带来的影响如下：
$$M_{z^{\prime }}\stackrel{{180^{\circ }}_{x^{\prime }}}{\to }-M_{z^{\prime }}\text{\hspace{1em}()}$$
$$M_{x^{\prime }{y}^{\prime }}\stackrel{{180^{\circ }}_{x^{\prime }}}{\to }-M_{x^{\prime }{y}^{\prime }}\text{\hspace{1em}()}$$

在$t=T_{I+}$时刻，即180°脉冲施加后，横向和纵向磁化强度分别为：
$$\begin{array}{rl}{M}_{z^{\prime }}(T_I+)& =-M_{z^{\prime }}({T_I}_{-})=-M_z^0\left(1-e^{-T_I/T_1}\right)\\ M_{x^{\prime }{y}^{\prime }}(T_I+)& =-M_{x^{\prime }{y}^{\prime }}({T_I}_{-})=-M_z^0{e}^{-T_I/T_2}\end{array}\text{\hspace{1em}()}$$

在$t>T_{I+}$时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}(t)& =M_z^0(1-e^{-(t-T_I)/T_1})-M_z^0\left(1-e^{-T_I/T_1}\right)e^{-(t-T_I)/T_1}& \\ & =M_z^0(1-e^{-(t-T_I)/T_1})-M_z^0\left(e^{-(t-T_I)/T_1}-e^{-t/T_1}\right)& \\ & =M_z^0(1-2e^{-(t-T_I)/T_1})+M_z^0{e}^{-t/T_1}& \\ & =M_z^0(1-2e^{-(t-T_I)/T_1}+e^{-t/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}(t)& =-M_z^0{e}^{-t/T_2}& \end{array}\text{\hspace{1em}()}$$

第2次饱和恢复：$T_R\le t<2T_R$

在$t={T_R}_{-}$时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}({T_R}_{-})& =M_z^0(1-2e^{-(T_R-T_I)/T_1}-e^{-T_R/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}({T_R}_{-})& =-M_z^0{e}^{-T_R/T_2}& \end{array}\text{\hspace{1em}()}$$

这里将$T_E=2T_I$代入上式，可得在时间$t={T_R}_{-}$时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}({T_R}_{-})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}({T_R}_{-})& =-M_z^0{e}^{-T_R/T_2}& \end{array}\text{\hspace{1em}()}$$
为了符号方便阅读，这里将${T_R}_{-}\to 0_{-}$，可得：
$$\begin{array}{rlr}{M}_{z^{\prime }}(0_{-})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}(0_{-})& =-M_z^0{e}^{-T_R/T_2}& \end{array}\text{\hspace{1em}()}$$

由于$T_2<T_E<<T_R$，所以上面的式子中横向磁化可以忽略不计。因此

在$t=0_{-}$时刻，即施加90°射频脉冲前，纵向和横向磁化强度分别为
$$\begin{array}{rlr}{M}_{z^{\prime }}(0_{-})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}(0_{-})& ～0& \end{array}\text{\hspace{1em}()}$$

在$t=0_{+}$时刻，即施加90°射频脉冲后，纵向和横向磁化强度分别为：
$$\begin{array}{rl}{M}_z^{\prime }(0_{+})& =0\\ M_{x^{\prime }{y}^{\prime }}(0_{+})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})\end{array}\text{\hspace{1em}()}$$

根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

在$0\le t<T_I$ 时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}(t)& =M_z^0\left(1-e^{-t/T_1}\right)& (0<t<T_I)\\ M_{x^{\prime }{y}^{\prime }}(t)& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})e^{-t/T_2}& (0<t<T_I)\end{array}\text{\hspace{1em}()}$$

在$t=T_{I-}$时刻，即180°脉冲施加前，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}({T_I}_{-})& =M_z^0\left(1-e^{-T_I/T_1}\right)& \\ M_{x^{\prime }{y}^{\prime }}({T_I}_{-})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})e^{-T_I/T_2}& \end{array}\text{\hspace{1em}()}$$

理想180°射频脉冲给横向和纵向磁化带来的影响如下：
$$M_{z^{\prime }}\stackrel{{180^{\circ }}_{x^{\prime }}}{\to }-M_{z^{\prime }}\text{\hspace{1em}()}$$
$$M_{x^{\prime }{y}^{\prime }}\stackrel{{180^{\circ }}_{x^{\prime }}}{\to }-M_{x^{\prime }{y}^{\prime }}\text{\hspace{1em}()}$$

在$t=T_{I+}$时刻，即180°脉冲施加后，横向和纵向磁化强度分别为：
$$\begin{array}{rl}{M}_{z^{\prime }}(T_I+)& =-M_{z^{\prime }}({T_I}_{-})=-M_z^0\left(1-e^{-T_I/T_1}\right)\\ M_{x^{\prime }{y}^{\prime }}(T_I+)& =-M_{x^{\prime }{y}^{\prime }}({T_I}_{-})=-M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})e^{-T_I/T_2}\end{array}\text{\hspace{1em}()}$$

在$t>T_{I+}$时刻，横向和纵向磁化强度分别为：
$$\begin{array}{rlr}{M}_{z^{\prime }}(t)& =M_z^0(1-e^{-(t-T_I)/T_1})-M_z^0\left(1-e^{-T_I/T_1}\right)e^{-(t-T_I)/T_1}& \\ & =M_z^0(1-e^{-(t-T_I)/T_1})-M_z^0\left(e^{-(t-T_I)/T_1}-e^{-t/T_1}\right)& \\ & =M_z^0(1-2e^{-(t-T_I)/T_1})+M_z^0{e}^{-t/T_1}& \\ & =M_z^0(1-2e^{-(t-T_I)/T_1}+e^{-t/T_1})& \\ & & \\ M_{x^{\prime }{y}^{\prime }}(t)& =-M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})e^{-t/T_2}& \end{array}\text{\hspace{1em}()}$$

由上式可得：

• 第一次循环后系统就已经进入了稳态，即后续的循环的起始时刻$t=0_{-}$时的纵向磁化强度都是：
  $$\begin{array}{rl}{M}_{z^{\prime }}(0_{-})& =M_z^0(1-2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1})\end{array}\text{\hspace{1em}(7.24)}$$

• 自旋回波信号的幅度可表示为：
  $$A_E=M_z^0\left(1-2e^{-(T_R-T_E/2)/T_1}+e^{-T_R/T_1}\right)e^{-T_E/T_2}\text{\hspace{1em}(7.25)}$$

在实际成像中，通常满足$T_E\ll T_R$的条件（即回波时间远小于重复时间）。在此条件下，可对公式(7.25)进行合理简化：当$T_E\ll T_R$时，有$T_R-T_E/2\approx T_R$，所以：
$$e^{-(T_R-T_E/2)/T_1}\approx e^{-T_R/T_1}$$

代入公式(7.25)得：
$$A_E=M_z^0\left(1-2e^{-T_R/T_1}+e^{-T_R/T_1}\right)e^{-T_E/T_2}=M_z^0\left(1-e^{-T_R/T_1}\right)e^{-T_E/T_2}\text{\hspace{1em}(7.26)}$$

选择性对比度强调

公式(7.26)表明，饱和恢复自旋回波序列的图像强度同时具有三种加权特性：

$T_1$加权对比度：采用短$T_E$和适当的$T_R$

• 短$T_E$使$e^{-T_E/T_2}\to 1$，消除$T_2$加权效应
• 适当$T_R$确保$(1-e^{-T_R/T_1})$产生明显的$T_1$对比

$T_2$加权对比度：采用长$T_E$和长$T_R$

• 长$T_R$使$(1-e^{-T_R/T_1})\to 1$，消除$T_1$加权效应
• 长$T_E$使$e^{-T_E/T_2}$产生明显的$T_2$对比

自旋密度加权对比度：采用短$T_E$和长$T_R$

• 短$T_E$消除$T_2$加权
• 长$T_R$消除$T_1$加权
• 剩余信号正比于自旋密度

下表总结了不同序列参数值对图像对比度的影响。

反转恢复自旋回波序列

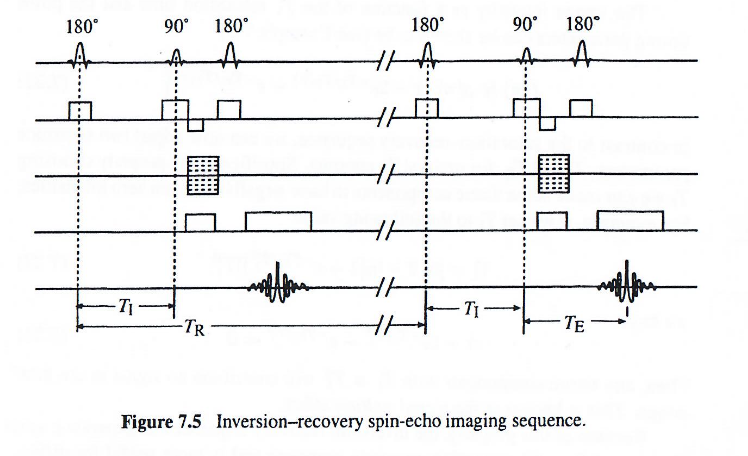
上展示了反转恢复自旋回波序列的时序图。该序列首先施加180°反转脉冲，随后在反转时间$T_I$后施加90°激发脉冲，最后通过180°重聚脉冲产生自旋回波。

对于反转恢复自旋回波序列，自旋回波信号的幅度可推导为：
$$A_E=M_z^0\left(1-2e^{-T_I/T_1}+2e^{-(T_R-T_E/2)/T_1}-e^{-T_R/T_1}\right)e^{-T_E/T_2}\text{\hspace{1em}(7.27)}$$

同样基于$T_E\ll T_R$的实用假设，公式(7.27)可简化为：
$$A_E=M_z^0\left(1-2e^{-T_I/T_1}+e^{-T_R/T_1}\right)e^{-T_E/T_2}\text{\hspace{1em}(7.28)}$$

该表达式表明，反转恢复自旋回波序列能够产生与饱和恢复自旋回波序列相似的$T_1$、$T_2$和自旋密度加权对比度，但具有更强的$T_1$对比度调控能力。

结论

基本自旋回波成像序列通过将自旋回波技术引入饱和恢复和反转恢复序列，实现了对图像对比度的精细调控。公式(7.24)至(7.28)完整描述了这些序列的信号特性，为临床MRI扫描参数优化提供了理论基础。

通过合理选择$T_R$、$T_E$和$T_I$等参数，可以获得满足特定诊断需求的图像对比度，这是自旋回波序列在临床磁共振成像中得以广泛应用的重要原因。