算法学习--快速幂
基本概念:
快速幂--模板

对于暴力解法--直接求a^b很容易出现超时以及存不下的问题(主要是超时问题),使用快速幂可以减少时间复杂度。
算法原理:假如要求5^10,对于幂数10我们使用二进制表示--1010,对于10可以看成2^3*2^1,5^10也就转化为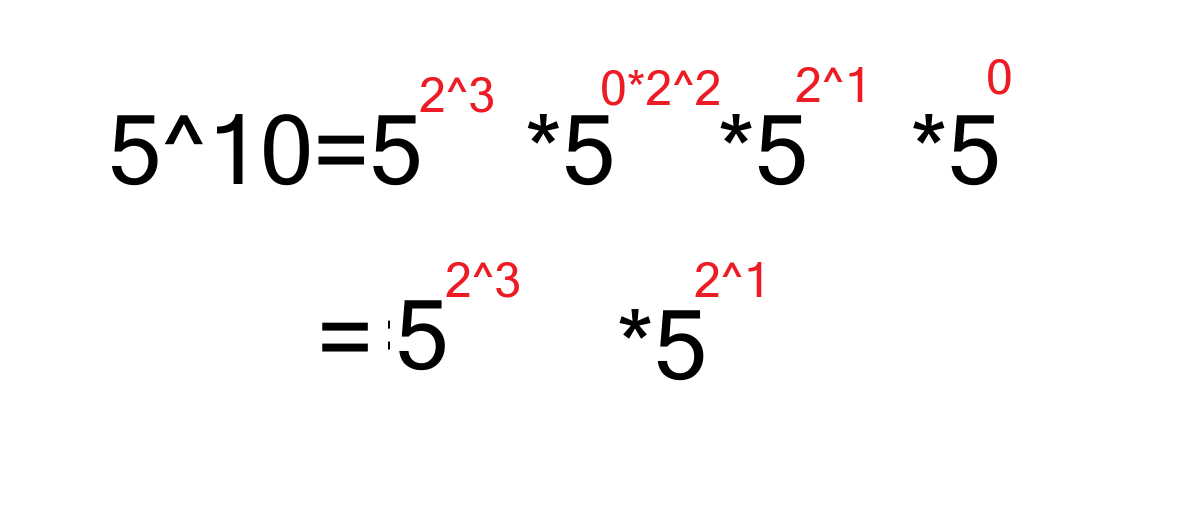
我们可以把这个计算过程看成5不断自乘(降低时间复杂度的核心),并且还只需要得到5^8和5^2这两个部分即可。既然是不断自乘,那又是怎么确定需要那些幂数呢,解决方法就是上面的二进制转化。
任何的数都能用二进制表示,我们把目标幂数看成二进制,在底数不断自乘的同时用位运算判断该处的权值是否需要计入,若为1就计入,否则为0不计入。
模板:
typedef long long ll;
ll calc(ll a,ll b,ll p)
{int ret=1;while(b){if(b&1){ret=(ret*a)%p;}a=a*a%p;b>>=1;}return ret%p;
}补充说明一下,底数自乘的过程中其幂是以二倍的方式递增,完全符合二进制右移后最后一位的权值变化。
模板题目中既然提到了取模运算,捎带手讲一讲。
取模运算中的技巧
常见的取模计算可分为三种:只有加法和乘法;存在减法;存在除法。由于存在除法时会涉及到后面的逆元,先说前面2中。
只有加法和乘法:
对于只有加法或乘法的情况下,取模可以放在任意位置(分配律)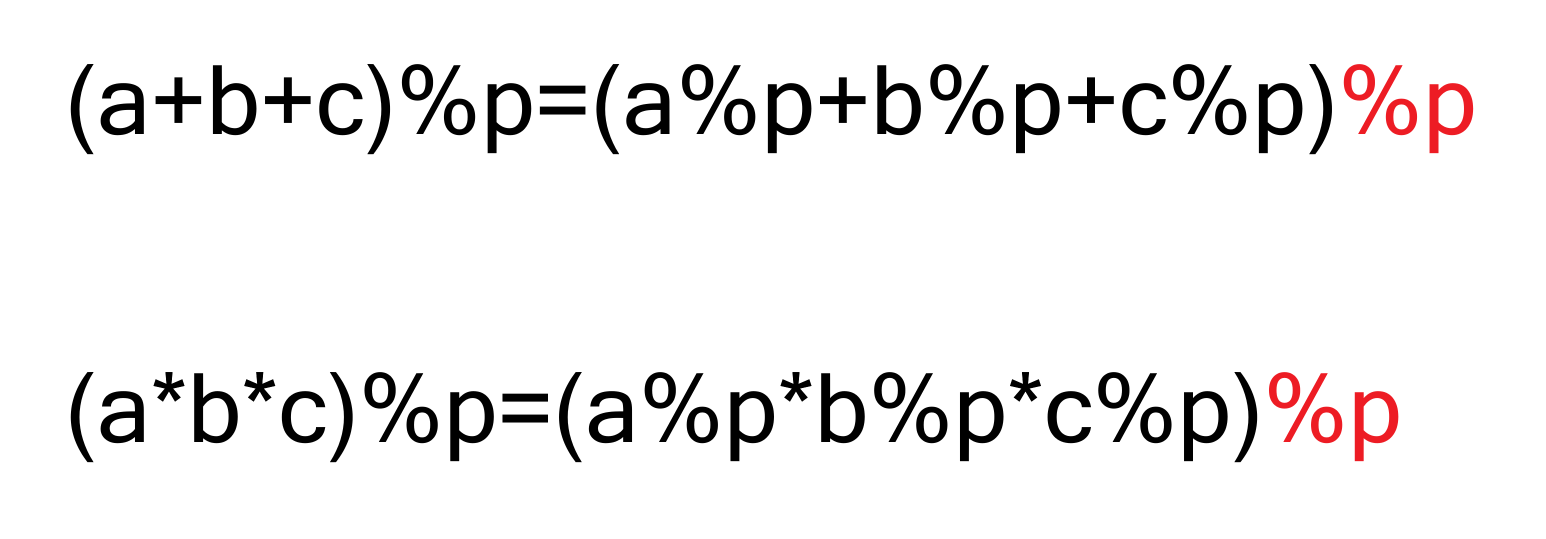
存在减法:
存在减法时可能会出现负数的情况,一旦出现底数为负数就要注意了,负数取模的处理在数学定义和计算机实现中存在差异
| 场景 | 数学定义(结果非负) | 计算机实现(不同语言有差异) |
|---|---|---|
示例:-5 % 3 | 数学上,-5 = 3×(-2) + 1,故结果为 1 | C++/Java 等语言中,结果为 -2(取商向零取整);Python 中,结果为 1(取商向下取整,符合数学定义) |
为了消除这种差异,我们需要对负数进行统一的 “模加模” 处理(肉夹馍):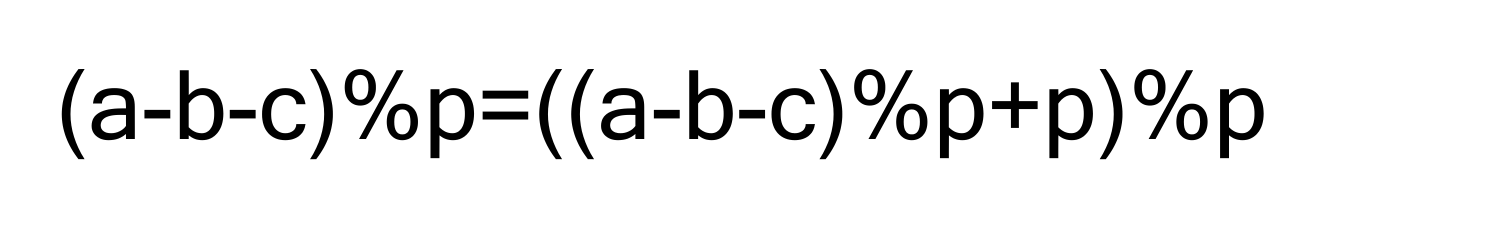
运用上面的技巧可以避免取模运算中的数据溢出问题。
另外,除了a^b这种形式,快速幂也有其它的“样式”,如a*b。
a*b,a*b我们先看成b个a之和,b同样也可以被转化为二进制,二进制的01同样能体现相关权值。唯一不同的就是由之前a为不断自乘变为a不断自加,后面还有可能会碰到a不断自减之类的情况。
总结
但是,总的来说其快速幂的思想并没有发生改变,依旧是依靠运算式中某一数(自己找)的二进制中的01表示相关的权值,当其具备目前权值时计入当前的自运算结果。
毕竟,快速幂的本质是 “二进制拆分 + 分步累积”嘛。
