磁共振成像原理（理论）35：快速梯度回波成像 (Fast Gradient-Echo Imaging)

本专题主要参考《Principles of Magnetic Resonance Imaging A Signal Processing Perspective 》-Sec 9.2

第7.5节已讨论了长重复时间（$T_R$）条件下的梯度回波成像，其通用脉冲序列如下图7.6所示。与传统自旋回波成像类似，梯度回波成像每次激发脉冲采集一条k空间线，因此若采用长$T_R$，无法实现显著的扫描速度提升。本节将重点讨论在极短重复时间（$T_R\ll T_2$）条件下运行的快速梯度回波成像方法。

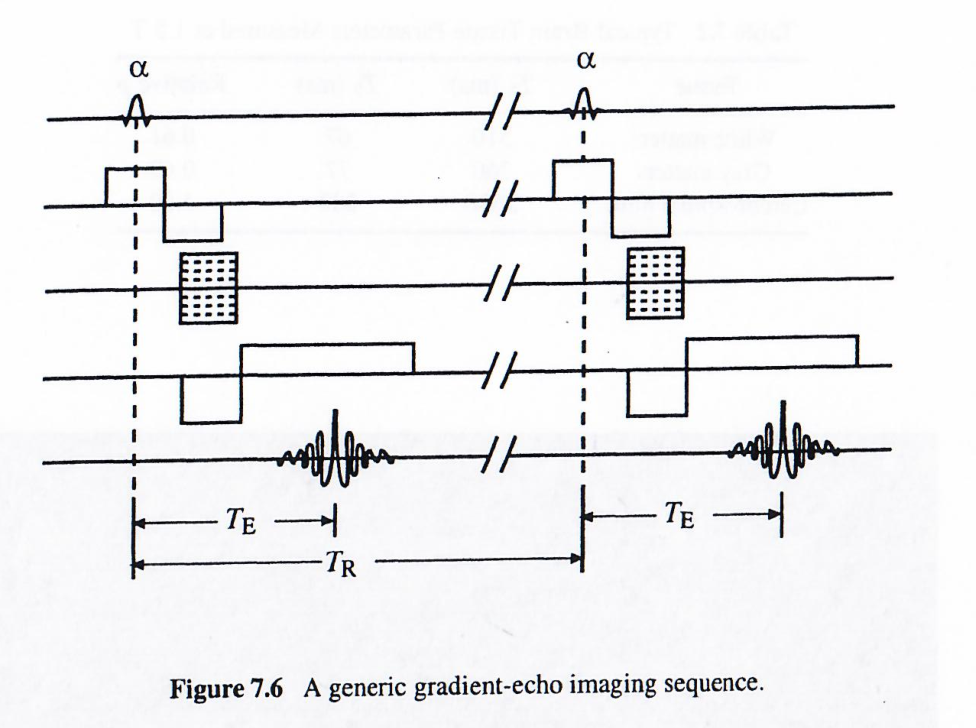
当自旋系统受到一系列周期性射频脉冲激发（满足$T_R\ll T_2$条件）时，系统将达到动态平衡状态，即所谓的稳态。目前已有多种稳态梯度回波成像序列被提出。根据每次激发后横向磁化矢量的处理方式，这些方法可分为两大类：扰相稳态成像方法和真实稳态成像方法。第一类方法建立稳态纵向磁化矢量，但在施加新射频脉冲前会破坏或"抑制"任何残余的横向磁化矢量；第二类方法则允许纵向和横向磁化矢量分量同时达到动态平衡状态。

扰相稳态成像

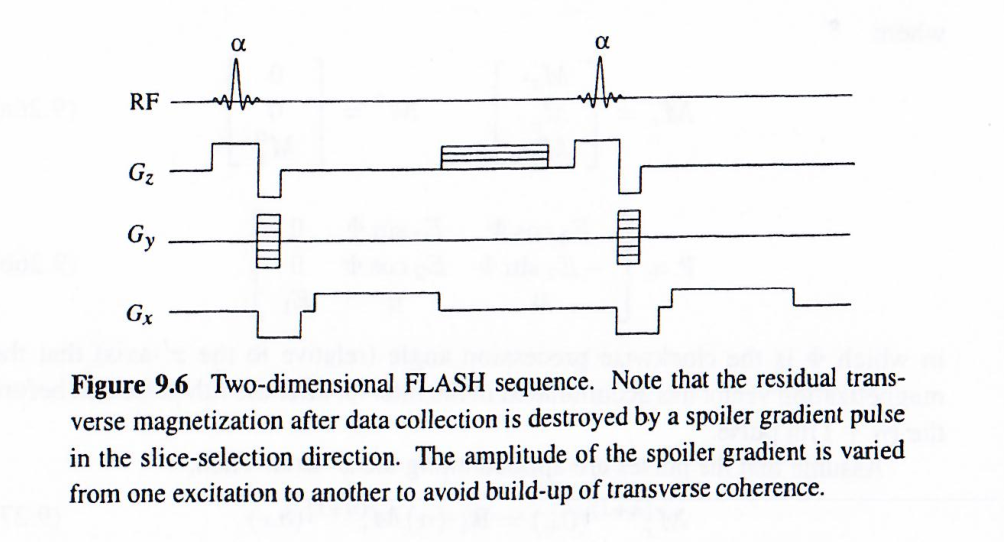
为理解扰相稳态成像的概念，我们以图9.6所示的FLASH（快速小角度激发）序列为例进行分析。该序列也称为扰相GRASS（稳态梯度重聚采集）序列。在此序列中，数据采集后的残余横向磁化矢量通过沿层选方向施加的扰相梯度脉冲进行消除。具体而言，扰相梯度的幅度在每次激发间进行变化，以避免横向磁化矢量的相干累积。扰相是本成像方案的关键要素。

接下来推导扰相稳态实验的信号表达式。在$T_R\ll T_2$条件下，当施加下一个脉冲时，前一个脉冲产生的横向磁化矢量尚未完全失相。采用扰相稳态成像方法时，该残余横向磁化矢量会通过各种扰相方法在施加新脉冲（假设$x^{\prime }$方向的$\alpha$脉冲）前被消除。因此，我们得到完美扰相条件（第n个脉冲激发前）：
$$M_{x^{\prime }{y}^{\prime }}^{(n)}(0_{-})=0\text{\hspace{1em}(9.12)}$$
让我们回顾一下之前的推导过程：

根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

我们得到纵向磁化强度的递推关系（第n-1个脉冲激发后到第n个脉冲激发前这段时间内的纵向磁化的演变）：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{(n-1)}(0_{+})e^{-T_R/T_1}\text{\hspace{1em}(7.30)}$$

其中$M_{z^{\prime }}^{(n)}(0_{-})$和$M_{z^{\prime }}^{(n-1)}(0_{+})$分别表示第n个脉冲前和第(n-1)个脉冲后的纵向磁化强度，两者的时间间隔就是$T_R$，所以将$t\to T_R$导入3.122即可得到式7.30。

利用$x^{\prime }$方向射频脉冲对纵向磁化强度的影响关系，见式3.91，重写如下：
$$R_{x^{\prime }}(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& -\sin \alpha & \cos \alpha \end{array}\right]\text{\hspace{1em}(3.91)}$$

因此得到了$\alpha$脉冲后的纵向磁化强度（注意脉冲前的横向磁化强度是0，见式子9.12，因为脉冲激发前已经完美扰相）：
$$M_{z^{\prime }}^{(n)}(0_{+})=M_{z^{\prime }}^{(n)}(0_{-})\cos \alpha \text{\hspace{1em}(7.31 A)}$$
$$M_{x^{\prime }{y}^{\prime }}^{(n)}(0_{+})=M_{z^{\prime }}^{(n)}(0_{-})\sin \alpha \text{\hspace{1em}(7.31 B)}$$
式(7.30)可以重写为：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{(n-1)}(0_{-})\cos \alpha \cdot e^{-T_R/T_1}\text{\hspace{1em}(7.32)}$$

当第n-1个脉冲激发前的纵向磁化强度$M_{z^{\prime }}^{(n-1)}(0_{-})$，等于第n个射频脉冲激发前的纵向磁化强度$M_{z^{\prime }}^{(n)}(0_{-})$时，此时系统达到动态稳态。假设这个值是$M_{z^{\prime }}^{ss}(0_{-})$，由此可得：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_{z^{\prime }}^{(n-1)}(0_{-})=M_{z^{\prime }}^{ss}(0_{-})\text{\hspace{1em}(7.33)}$$

将稳态条件代入式(7.32)，得到：
$$M_{z^{\prime }}^{ss}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{ss}(0_{-})\cos \alpha \cdot e^{-T_R/T_1}\text{\hspace{1em}()}$$

整理后求解稳态纵向磁化强度：
$$M_{z^{\prime }}^{ss}(0_{-})(1-\cos \alpha \cdot e^{-T_R/T_1})=M_z^0(1-e^{-T_R/T_1})\text{\hspace{1em}()}$$

即
$$M_{z^{\prime }}^{ss}(0_{-})=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\text{\hspace{1em}(7.34)}$$
回顾完毕，回到本章节。因此，当实现完美扰相时，激发后的横向强度$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})$和激发前的纵向磁化强度$M_{z^{\prime }}^{ss}(0_{-})$的稳态值分别是：
$$M_{z^{\prime }}^{ss}(0_{-})=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\text{\hspace{1em}(9.13)}$$

$$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})=M_{z^{\prime }}^{ss}(0_{-})\sin \alpha =\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\sin \alpha \text{\hspace{1em}(9.14)}$$

方程(9.13)和(9.14)表明，扰相稳态信号的幅度取决于翻转角$\alpha$和重复时间$T_R$。对于固定的$T_R$，可通过适当选择$\alpha$来最大化$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{-})$。这个最优角度即著名的恩斯特角，记为${\alpha }_E$：
$$\cos {\alpha }_E=e^{-T_R/T_1}\text{\hspace{1em}(9.15)}$$

或等价表示为：
$${\alpha }_E={\cos }^{-1}\left(e^{-T_R/T_1}\right)\text{\hspace{1em}(9.16)}$$

在稳态成像实验中，理想情况应在系统达到稳态后开始数据采集。接下来评估自旋系统达到扰相稳态所需的脉冲数。

回顾第n个脉冲前的纵向磁化矢量表达式：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-e^{-T_R/T_1})+M_{z^{\prime }}^{(n-1)}(0_{-})\cos \alpha \cdot e^{-T_R/T_1}\text{\hspace{1em}(9.17)}$$

引入变量简化表达：
$$\{\begin{array}{l}{E}_1=e^{-T_R/T_1}\\ E_2=e^{-T_R/T_2}\end{array}\text{\hspace{1em}(9.18)}$$

则方程(9.17)可改写为：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-E_1)+M_{z^{\prime }}^{(n-1)}(0_{-})\cos \alpha \cdot E_1\text{\hspace{1em}(9.19)}$$

求解该差分方程可得：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0(1-E_1)\frac{1-(\cos \alpha \cdot E_1{)}^n}{1-\cos \alpha \cdot E_1}+M_z^0(\cos \alpha \cdot E_1{)}^n(n\ge 1)\text{\hspace{1em}(9.20)}$$

收敛误差定义为$M_{z^{\prime }}^{(n)}(0_{-})$与期望稳态值的差值：

$$\begin{array}{rl}\Delta M_{z^{\prime }}^{(n)}(0_{-})& =M_{z^{\prime }}^{(n)}(0_{-})-M_{z^{\prime }}^{ss}(0_{-})\\ & =M_z^0\frac{(\cos \alpha \cdot E_1{)}^n{E}_1(1-\cos \alpha )}{1-\cos \alpha \cdot E_1}\end{array}\text{\hspace{1em}(9.21)}$$

相对收敛误差为：
$$\frac{\Delta M_{z^{\prime }}^{(n)}(0_{-})}{M_{z^{\prime }}^{ss}(0_{-})}=\frac{(\cos \alpha \cdot E_1{)}^n{E}_1(1-\cos \alpha )}{1-E_1}\text{\hspace{1em}(9.22)}$$

当$\alpha ={\alpha }_E$时，计算可简化为：
$$\frac{\Delta M_{z^{\prime }}^{(n)}(0_{-})}{M_{z^{\prime }}^{ss}(0_{-})}=E_1^{2n+1}\text{\hspace{1em}(9.23)}$$

或者可以写成
$$\begin{array}{rl}n& =\frac{T_1}{2T_R}\ln \left(\frac{\Delta M_{z^{\prime }}^{(n)}(0_{-})}{M_{z^{\prime }}^{ss}(0_{-})}\right)-\frac{1}{2}\end{array}$$

扰相稳态成像的图像对比度特性可从方程(9.14)理解。梯度回波幅度可表示为：
$$A_E=\frac{M_z^0(1-e^{-T_R/T_1})}{1-\cos \alpha \cdot e^{-T_R/T_1}}\sin \alpha \cdot e^{-T_E/T_2^{\ast }}\text{\hspace{1em}(9.24)}$$

注意：上面用的是$T_2^{\ast }$，而不是$T_2$，因为回波是在有频率编码梯度的情况下采集的。

示例1

脑白质在1.5T场强下的$T_1$值约为600ms。假设$T_R=40$ms，计算${\alpha }_E$以及使$M_{z^{\prime }}^{(n)}(0_{-})$达到稳态值99%所需的脉冲数。

根据方程(9.16)计算恩斯特角：
$${\alpha }_E={\cos }^{-1}\left(e^{-40/600}\right)=20.7^{\circ }$$

根据方程(9.23)计算所需脉冲数：
$$\begin{array}{rl}n& =\frac{T_1}{2T_R}\ln \left(\frac{\Delta M_{z^{\prime }}^{(n)}(0_{-})}{M_{z^{\prime }}^{ss}(0_{-})}\right)-\frac{1}{2}\\ & =\frac{600}{2\times 40}\ln (0.01)-\frac{1}{2}\approx 34\end{array}$$

因此，约需要34个预备脉冲才能使$M_{z^{\prime }}^{(n)}(0_{-})$达到其稳态值的99%。

真实稳态成像

当$T_R$与$T_2$相当时，且不破坏横向磁化时，纵向和横向磁化将同时达到稳态。这种现象称为稳态自由进动（SSFP），由Carr于1958年首次研究。

首先推导SSFP信号的表达式。定义$E_1=e^{-T_R/T_1}$，$E_2=e^{-T_R/T_2}$。第(n+1)个脉冲(假设为$z^{\prime }$方向)前的磁化与第n个脉冲后的磁化关系为：
$$M_r^{(n+1)}(0_{-})=P{M}_r^{(n)}(0_{+})+(1-E_1)M^0\text{\hspace{1em}(9.25)}$$

其中：
$$M_r=\left[\begin{array}{c}{M}_{x^{\prime }}\\ M_{y^{\prime }}\\ M_{z^{\prime }}\end{array}\right],M^0=\left[\begin{array}{c}0\\ 0\\ M_z^0\end{array}\right]\text{\hspace{1em}(9.26a)}$$

$$P=\left[\begin{array}{ccc}{E}_2\cos \Phi & E_2\sin \Phi & 0\\ -E_2\sin \Phi & E_2\cos \Phi & 0\\ 0& 0& E_1\end{array}\right]\text{\hspace{1em}(9.26b)}$$

其中$\Phi$是磁化矢量在第n个脉冲后与第(n+1)个脉冲前累积的顺时针进动角（相对于$x^{\prime }$轴的转角）。

假设脉冲沿$x^{\prime }$轴施加，则：
$$M_r^{(n+1)}(0_{+})=R_{x^{\prime }}(\alpha )M_r^{(n+1)}(0_{-})\text{\hspace{1em}(9.27)}$$

代入方程(9.25)得：
$$M_r^{(n+1)}(0_{+})=R_{x^{\prime }}(\alpha )P{M}_r^{(n)}(0_{+})+(1-E_1)R_{x^{\prime }}(\alpha )M^0\text{\hspace{1em}(9.28)}$$

类似地，可推导：
$$M_r^{(n+1)}(0_{-})=P{R}_{x^{\prime }}(\alpha )M_r^{(n)}(0_{-})+(1-E_1)M^0\text{\hspace{1em}(9.29)}$$

设稳态条件：
$$M_r^{(n+1)}(0_{-})=M_r^{(n)}(0_{-})=M_r^{ss}(0_{-})\text{\hspace{1em}(9.30a)}$$
$$M_r^{(n+1)}(0_{+})=M_r^{(n)}(0_{+})=M_r^{ss}(0_{+})\text{\hspace{1em}(9.30b)}$$

得到稳态磁化的控制方程：
$$M_r^{ss}(0_{-})=P{R}_{x^{\prime }}(\alpha )M_r^{ss}(0_{+})+(1-E_1)M^0\text{\hspace{1em}(9.31a)}$$
$$M_r^{ss}(0_{+})=R_{x^{\prime }}(\alpha )P{M}_r^{ss}(0_{+})+(1-E_1)R_{x^{\prime }}(\alpha )M^0\text{\hspace{1em}(9.31b)}$$

方程的解为：
$$M_r^{ss}(0_{-})=(1-E_1)[I-P{R}_{x^{\prime }}(\alpha ){]}^{-1}{M}^0\text{\hspace{1em}(9.32a)}$$
$$M_r^{ss}(0_{+})=(1-E_1)[I-R_{x^{\prime }}(\alpha )P{]}^{-1}{R}_{x^{\prime }}(\alpha )M^0\text{\hspace{1em}(9.32b)}$$

其中$I$是3×3单位矩阵。这些解可明确写为：
$$\{\begin{array}{l}{M}_{x^{\prime }}(0_{-})=M_z^0(1-E_1)E_2\sin \alpha \sin \Phi /D\\ M_{y^{\prime }}(0_{-})=M_z^0(1-E_1)(E_2\sin \alpha \cos \Phi -E_2^2\sin \alpha )/D\\ M_{z^{\prime }}(0_{-})=M_z^0(1-E_1)[1-E_2\cos \Phi -E_2\cos \alpha (\cos \Phi -E_2)]/D\end{array}\text{\hspace{1em}(9.33)}$$

和
$$\{\begin{array}{l}{M}_{x^{\prime }}(0_{+})=M_z^0(1-E_1)E_2\sin \alpha \sin \Phi /D\\ M_{y^{\prime }}(0_{+})=M_z^0(1-E_1)(1-E_2\cos \Phi )\sin \alpha /D\\ M_{z^{\prime }}(0_{+})=M_z^0(1-E_1)[E_2(E_2-\cos \Phi )+(1-E_2\cos \Phi )\cos \Phi ]/D\end{array}\text{\hspace{1em}(9.34)}$$

其中：
$$D=(1-E_1\cos \alpha )(1-E_2\cos \Phi )-(E_1-\cos \alpha )(E_2-\cos \Phi )E_2\text{\hspace{1em}(9.35)}$$

方程(9.34)显示SSFP信号是$\alpha$、$E_1$、$E_2$和$\Phi$的复杂函数。Ernst和Anderson发现产生最大横向磁化的最优翻转角为：
$$\cos {\alpha }_{opt}=\frac{E_1+E_2(\cos \Phi -E_2)/(1-E_2\cos \Phi )}{1+E_1{E}_2(\cos \Phi -E_2)/(1-E_2\cos \Phi )}\text{\hspace{1em}(9.36)}$$

可通过将$M_{y^{\prime }}^{ss}(0_{+})$对$\alpha$求导并令结果为零得到此表达式。可以证明：
$${\frac{d{M}_{x^{\prime }}^{ss}(0_{+})}{d\alpha }|}_{\alpha ={\alpha }_{opt}}={\frac{d{M}_{y^{\prime }}^{ss}(0_{+})}{d\alpha }|}_{\alpha ={\alpha }_{opt}}={\frac{d{M}_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})}{d\alpha }|}_{\alpha ={\alpha }_{opt}}=0\text{\hspace{1em}(9.37)}$$

许多稳态成像方法已被提出并具有实际用途。作为示例，图9.7显示了二维FISP（稳态进动快速成像）序列。与图9.6中的FLASH序列相比，FISP序列中的成像梯度完全平衡，因此每个成像梯度的净效应在激发周期间保持恒定。

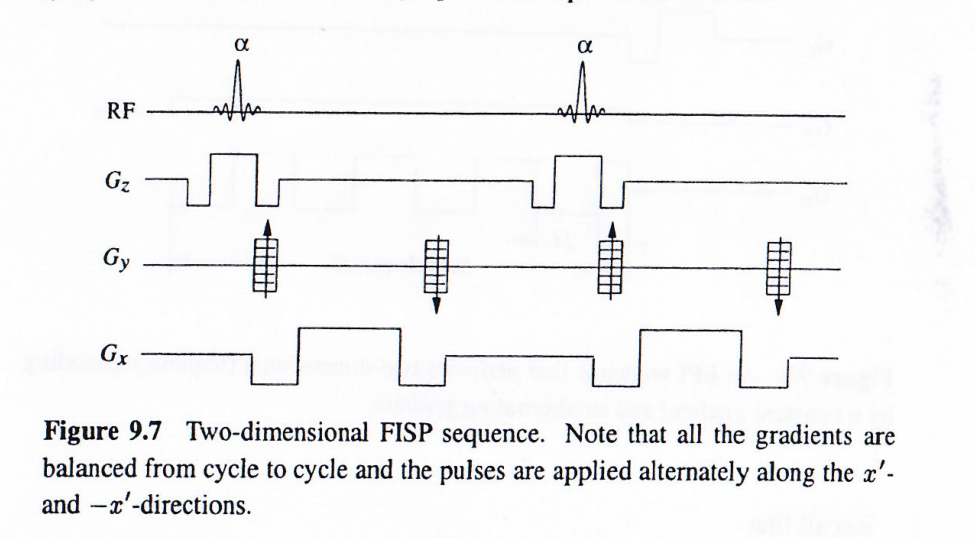
为理解此成像方案的对比度行为，我们检查$\Phi =\pi$的特殊情况。该条件通过交替脉冲和可忽略的场不均匀性实现。在此条件下，$M_{x^{\prime }}(0_{+})=0$，且：

$$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})=M_{y^{\prime }}^{ss}(0_{+})=\frac{M_z^0(1-E_1)\sin \alpha }{(1-E_1\cos \alpha )-E_2(E_1-\cos \alpha )}\text{\hspace{1em}(9.38)}$$

对于$T_R\ll T_2,T_1$，可应用以下近似：

$$E_1\approx 1-\frac{T_R}{T_1}\text{\hspace{1em}(9.39a)}$$

$$E_2\approx 1-\frac{T_R}{T_2}\text{\hspace{1em}(9.39b)}$$

因此，方程(9.38)可重写为：

$$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})=\frac{M_z^0\sin \alpha }{1+T_1/T_2-(T_1/T_2-1)\cos \alpha }\text{\hspace{1em}(9.40)}$$

对于$\alpha =90^{\circ }$，方程(9.40)简化为：

$$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})=M_z^0\frac{T_2}{T_1+T_2}\text{\hspace{1em}(9.41)}$$

或进一步简化为：

$$M_{x^{\prime }{y}^{\prime }}^{ss}(0_{+})=M_z^0\frac{T_2}{T_1}\text{\hspace{1em}(9.42)}$$

注意到$T_1\gg T_2$。方程(9.41)和(9.42)表明FISP图像具有$T_2/T_1$对比度。因此，FISP从具有长$T_2$和短$T_1$的组织产生强信号。对于$T_R\ll T_2$，FISP信号基本上与$T_R$值无关。这意味着FISP可以在非常短的$T_R$下运行而不会牺牲信噪比，这是稳态成像的独特特性。