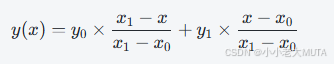语义分割中上采样Up-sampling的原理

参考视频：面试必刷：语义分割中上采样（Upsampling）的原理是什么？_哔哩哔哩_bilibili

回答思路

1. 为什么以及如何将低分辨率特征恢复为高分辨率输出？

2. 如何通过反卷积和跳跃连接实现细节重建？

3. 为什么上采样在分割任务中至关重要？

---

为什么需要恢复高分辨率？

语义分割任务的目标是对输入图像中的每个像素进行分类，输出图像尺寸需与输入保持一致，保证像素级别的精确预测。

而在编码（下采样）阶段，为了提取更丰富的语义信息，网络会逐步降低特征图的空间分辨率，这导致输出的特征图尺寸远小于输入尺寸。

因此，需要将这些低分辨率的语义特征“放大”回高分辨率，方便得到像素级的预测。

如何实现恢复？

上采样是将低分辨率特征图恢复到高分辨率的过程。常用方法包括：

• 插值法（如双线性插值）：简单快速，但对细节恢复有限。
• 转置卷积（反卷积）：通过学习参数的卷积核，将特征图空间放大，同时提取更丰富特征。
• 子像素卷积：通过重排通道实现空间放大。
• 无参数上采样 + 卷积：先插值放大再卷积，兼顾效率和效果。

如何通过反卷积和跳跃连接实现细节重建？

反卷积负责恢复空间分辨率且增强语义特征，跳跃连接补充空间细节，二者结合使得解码器能重建出更精细、准确的分割边界和物体结构。

为什么上采样在分割任务中至关重要？

语义分割需要对每个像素分类，输出保持输入尺寸。上采样是唯一使特征恢复到输入空间维度的操作，保证预测的空间一致性。上采样帮助网络将高层语义信息映射回空间维度，同时结合跳跃连接携带的空间细节，实现语义与空间的有机结合。

---

知识点

线性插值

核心思想：在两个已知数据点之间构造一条直线，根据横坐标位置在线段上的比例，计算该位置对应的函数值（像素值）。

目标点的值是相邻点的加权平均，权重与目标点与已知点的距离成反比。

一维线性插值

假设已知两个点 (x0,y0) 和 (x1,y1)，要估计 x∈(x0,x1) 处的函数值 y(x)，可用：

即根据距离比例对两个端点值做线性加权。

二维线性插值

转置卷积（反卷积）

详情请看：膨胀卷积（空洞卷积）和转置卷积（反卷积）_dilation conv-CSDN博客

转置卷积的作用是：根据输入特征图和卷积核，生成一个比输入更大空间尺寸的输出，实现空间分辨率的上采样。

与普通卷积（下采样或维持尺寸）不同，转置卷积通过插入“空洞”或零填充的方式，将输入映射到更大尺寸的输出。

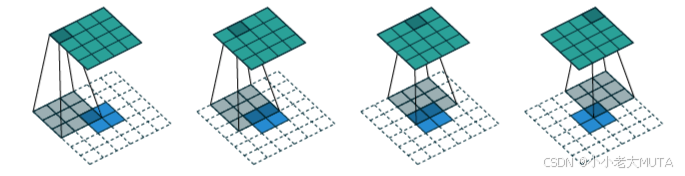
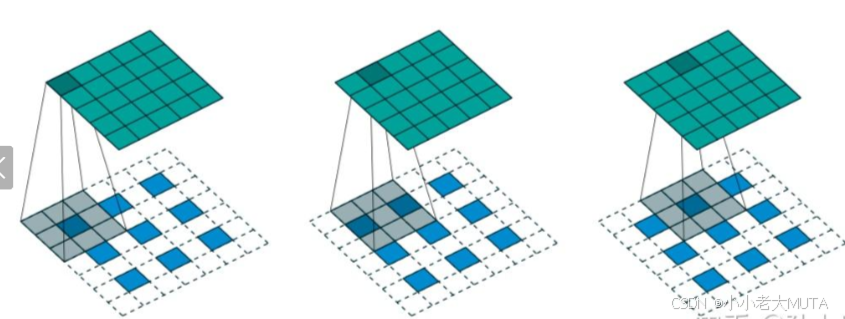
直观理解

普通卷积是“卷积核在输入上滑动取加权和”

转置卷积是“将输入的每个元素乘以卷积核，放置到对应的位置，然后重叠相加”

为什么叫转置卷积？

转置卷积的名称来源于它与普通卷积在矩阵乘法表现形式上的转置关系。

本质上是普通卷积的“逆过程”，但并不是真正的数学逆运算，而是通过特定方式实现空间上的“扩张”。

跳跃连接

语义分割网络通常采用“编码器-解码器”架构，编码器负责逐步降低空间分辨率，提取高层次语义特征；解码器负责逐步上采样，恢复空间分辨率。

如下图所示，就是经典的U-Net网络：

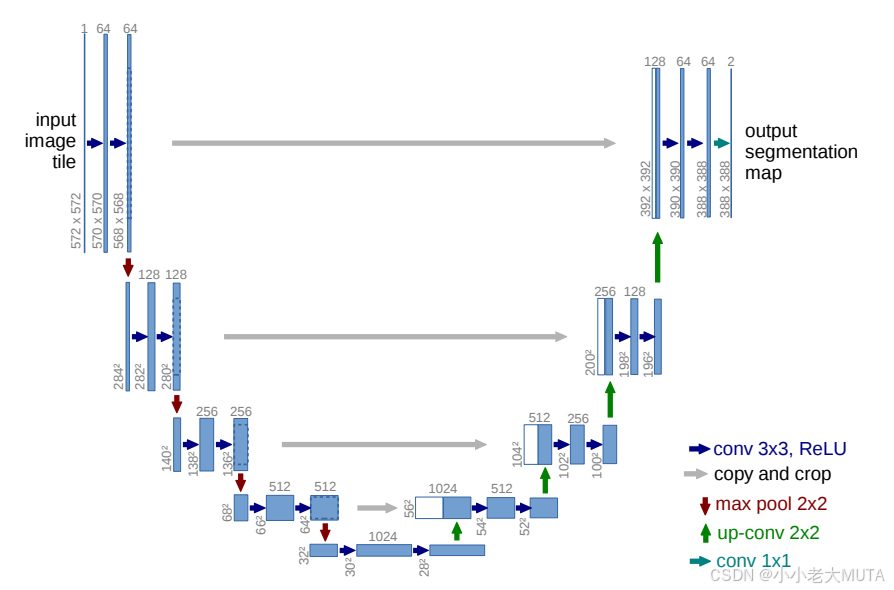
跳跃连接是指在网络中，将编码器某一中间层的特征图直接传递（跳过若干层）给伽玛琪对应分辨率的特征图，并融合使用。在上图就是中间灰色的横线箭头表示的意思。

跳跃连接的核心作用

• 补充空间细节信息：浅层特征保留了较丰富的边缘、纹理等细节信息，弥补深层上采样后的模糊。
• 缓解梯度消失，促进训练：跳跃连接提供了梯度的直接传递路径，帮助网络更好地训练。

---