NeurIPS 2025 中科大等提出PIR：实例感知后处理修正框架，显著提升时序预测可靠性！

在交通规划、天气预报等众多领域，时间序列预测技术都扮演着关键角色。尽管现有的深度学习模型在总体预测精度上取得了显著成功，但它们往往忽略了实例级的变化——即便是性能强大的模型，在面对一些由数据分布偏移、数据缺失或罕见模式导致的特殊情况时，也可能做出糟糕的预测。这导致了模型在某些特定时刻的预测结果并不可靠，形成了性能表现上的“长尾问题”。

为了解决这一难题，本论文提出了一个名为PIR，即事后识别与修正的预测增强框架。该框架首先通过评估预测结果的不确定性来“识别”出那些可能出错的预测，然后从“局部”和“全局”两个维度利用上下文信息来“修正”它们。实验证明，PIR框架能够作为一个通用插件，显著提升多种主流预测模型的性能和可靠性。

另外我整理了NeurIPS 2025时间序列相关论文+源码合集，感兴趣的可以自取，希望能帮到你！

原文 资料 这里！

一、论文基本信息

论文标题： Improving Time Series Forecasting via Instance-aware Post-hoc Revision

作者姓名： Zhiding Liu, Mingyue Cheng, Guanhao Zhao, Jiqian Yang, Qi Liu, Enhong Chen

作者单位/机构： 中国科学技术大学，认知智能全国重点实验室

论文链接： https://arxiv.org/abs/2405.23583

论文代码： https://github.com/icantnamemyself/PIR

二、主要贡献与创新

1. 首次揭示并关注了时间序列预测中存在的实例级变化，并指出其是导致模型在特定情况下预测失败的关键原因。
2. 提出了一个创新的模型无关框架PIR，通过“先识别，后修正”的后处理范式来应对这一挑战。
3. 巧妙地设计了局部与全局相结合的修正机制，全面利用协变量、外部信息和历史数据来提升预测的鲁棒性。
4. PIR作为一个即插即用的模块，无需改动现有模型结构，具有极强的通用性和实际应用价值。

三、研究方法与原理

PIR模型的核心思路是：先利用不确定性估计来识别出初始预测结果中可能存在的“坏”预测，然后结合局部上下文与全局相似历史数据，对这些预测进行针对性修正。

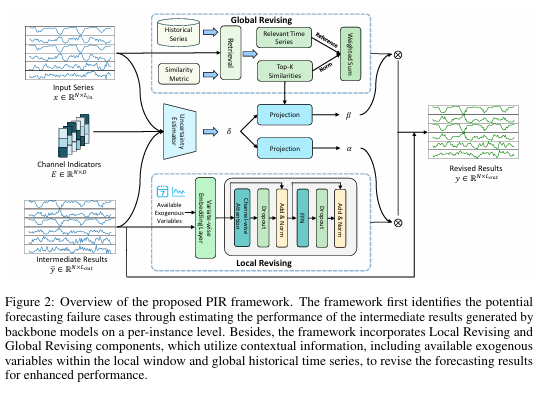
整个框架由三个关键模块组成：失败识别（Failure Identification）、局部修正（Local Revising）和全局修正（Global Revising）。

失败识别模块

这个模块的目标是在没有真实标签的情况下，判断一个由基础模型给出的预测结果 $\bar{y}$ 有多大的可能会出错。作者创新地将这个问题转化为一个不确定性估计 (Uncertainty Estimation) 任务。其核心思想是，一个预测的不确定性越高，其产生的预测误差可能就越大。

因此，作者设计了一个简单的神经网络 $f_{ue}(\cdot )$ 来估计每个预测实例的不确定度 $\delta$。为了让这个估计更准确，他们引入了一个辅助约束，即让估计出的不确定度 $\delta$ 去逼近该实例真实的均方误差 (Mean Squared Error, MSE) 。具体公式如下：
$$\begin{gathered} \delta =f_{ue}(x,\bar{y},E), \\ {\mathcal{L}}_{ue}=\frac{1}{N}\sum _1^N\Vert \delta -\Vert \bar{y}-y{\Vert }_2^2{\Vert }_1 \end{gathered}$$
其中，$x$ 是输入序列，$\bar{y}$ 是基础模型的预测结果，$y$ 是真实值。$E$ 是一个通道嵌入矩阵，用于提供不同变量的身份信息。损失函数 ${\mathcal{L}}_{ue}$ 采用平均绝对误差 (Mean Absolute Error, MAE) 来衡量估计的不确定度与真实误差之间的差距。通过这种方式，模型学会了如何为每个预测实例“打分”，分数越高（即$\delta$越大），代表这个预测越不可靠，越需要被修正。

局部修正模块

当识别出某个预测可能不准后，PIR会首先尝试从“局部”寻找修正线索。这里的“局部”指的是与当前预测时间窗口紧密相关的上下文信息，主要包括协变量 (covariates) 和外生变量 (exogenous variables)。例如，在预测某个地区的用电量时，同一时间其他地区的用电量（协变量）以及节假日信息（外生变量）都能提供有价值的参考。

具体实现上，该模块将基础模型对协变量的中间预测结果 $\bar{y}$ 以及编码后的外生变量信息 $c$ 进行拼接，然后送入一个标准的Transformer模型中。该过程可由以下公式表示：
$$\begin{gathered} H^0=[h_{co},h_{exo}], \\ {h}_{co}=\text{CoVariateEmb}(\bar{y}), \\ {h}_{exo}=\text{ExoVariateEmb}(c) \end{gathered}$$
通过Transformer强大的自注意力机制，模型可以捕捉这些局部信息之间的复杂依赖关系，从而生成一个修正项 $y_{local}$，用于纠正原始预测中可能存在的偏差。

原文 资料 这里！

全局修正模块

局部修正虽然有效，但如果遇到非常罕见或从未见过的模式，它可能也无能为力。为此，PIR引入了全局修正模块，其核心思想是从海量的历史数据中寻找与当前情况相似的“历史经验”。

该模块首先会构建一个仅包含训练数据的“历史数据库”。当需要修正一个新的预测实例 $x$ 时，它会通过计算相似度（如余弦相似度）从数据库中检索出Top-K个最相似的历史输入序列，其过程如下：
$$\text{Index},w=\text{TopKSim}(\text{Enc}(x),\text{Enc}(X))$$
其中，$\text{Enc}(\cdot )$ 是一个编码函数，用于提取序列的关键特征。找到这K个最相似的历史输入后，模型会取出它们对应的真实未来序列 $Y_{re}$。基于一个合理的假设——相似的过去预示着相似的未来——模型将这K个历史未来序列根据其相似度得分 $w$ 进行加权平均，从而得到一个全局修正项 $y_{global}$：
$$\begin{gathered} p=\text{Softmax}(w), \\ {y}_{global}=\text{WeightedSum}(p,Y_{re}) \end{gathered}$$
这个全局修正项为模型应对长尾分布中的罕见模式提供了强有力的支持。

最终优化

最后，PIR将基础模型的原始预测 $\bar{y}$、局部修正项 $y_{local}$ 和全局修正项 $y_{global}$ 进行动态加权融合，得到最终的预测结果 $y_{pred}$。
$$y_{pred}=\bar{y}+\alpha y_{local}+\beta y_{global}$$
这里的权重 $\alpha$ 和 $\beta$ 不是固定的，而是由失败识别模块估计出的不确定度 $\delta$ 动态生成的。具体来说，当不确定度 $\delta$ 越高时，模型会赋予修正项更大的权重。整个框架通过一个联合优化的损失函数 $\mathcal{L}={\mathcal{L}}_{pr}+\lambda {\mathcal{L}}_{ue}$ 进行端到端的训练，其中 ${\mathcal{L}}_{pr}$ 是最终预测结果的MSE损失。

四、实验设计与结果分析

论文在多个公开基准数据集上进行了详尽的实验，这些数据集覆盖了能源、交通、天气等多个领域，包括用于长期预测的ETTh1/2, ETTm1/2, Electricity, Weather等，以及用于短期预测的PEMS系列数据集。实验选择了四种不同架构的主流模型（PatchTST, SparseTSF, iTransformer, TimeMixer）作为基础模型，以验证PIR框架的通用性。评价指标为MSE和MAE。

对比实验

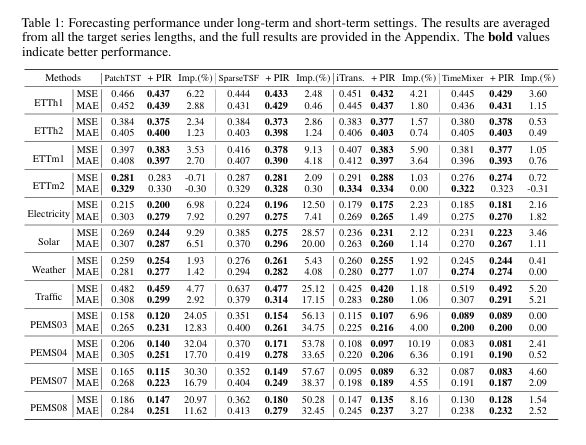
表1展示了PIR框架在集成到四种不同基础模型后，在12个数据集上的性能对比。从结果中可以清晰地看到，PIR几乎在所有场景下都为基础模型带来了性能提升。例如，它为PatchTST带来了平均8.99%的MSE下降，为SparseTSF带来了高达25.87%的MSE下降。这一结果有力地证明了PIR框架的有效性和通用性。

值得注意的是，相较于iTransformer这类本身就考虑了通道间依赖（即利用了协变量信息）的模型，PIR在PatchTST和SparseTSF这类通道独立模型上的提升更为显著。这说明PIR的局部修正模块有效地弥补了这些模型在上下文信息利用上的不足，同时也证明了即使对于已经很强的模型，PIR依然能通过其独特的识别修正机制发掘提升空间。

可视化对比

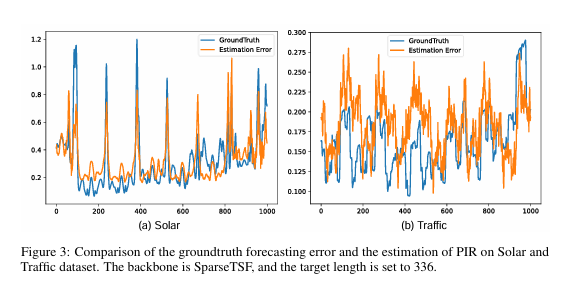
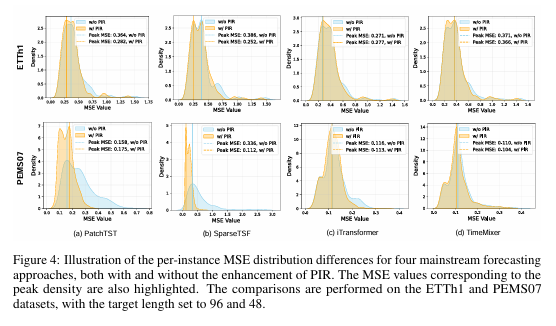
为了更直观地展示PIR的工作原理和效果，论文进行了定性分析。

在图3中，作者对比了PIR估计的预测误差与真实的预测误差。可以看出，两条曲线的峰谷走势高度一致，这表明PIR的失败识别模块能够准确地判断出哪些预测实例的质量较差，为后续的精准修正奠定了坚实基础。

在图4中，作者展示了加入PIR前后，模型在每个实例上的MSE分布变化。可以观察到，经过PIR增强后，误差分布曲线明显向左侧（低误差区域）偏移，且峰值更高，意味着绝大多数实例的预测都变得更加准确。同时，曲线的“长尾”也变得更短，说明那些原本预测得非常糟糕的极端情况得到了有效修正。例如，在PEMS07数据集上，模型预测误差的尾部被显著拉回，展示了PIR在提升预测可靠性方面的强大能力。

消融实验

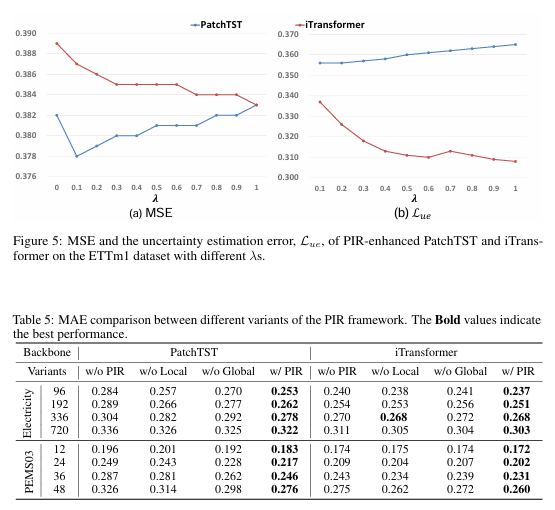
在论文附录的表5和图5中，作者进行了消融研究，以验证框架中各个组件的必要性。

表5分别移除了局部修正模块（w/o Local）和全局修正模块（w/o Global）进行对比。结果显示，单独使用任何一个修正模块都能带来一定的性能提升，而将两者结合使用时效果最好。这证明了局部和全局修正分别从不同角度提供了有益信息，二者相辅相成。

图5则探讨了失败识别模块中辅助约束的重要性。实验表明，当约束权重 $\lambda >0$ 时，模型的不确定性估计误差 ${\mathcal{L}}_{ue}$ 更低，最终的预测精度也更高。这证实了通过预测误差来指导不确定性估计是一种有效的设计。

五、论文结论与评价

总结

本文深入探讨了时间序列预测中普遍存在但常被忽视的实例级变化问题，并创新性地提出了一个模型无关的后处理框架PIR。理论上，它通过一种将不确定性估计与预测误差相关联的巧妙机制来识别潜在的预测失败案例，并结合局部与全局上下文信息进行双重修正。实验上，PIR在多个数据集和多种基础模型上都取得了显著的性能提升，证明了其作为一个通用插件的有效性和强大潜力。这项工作为提升时间序列预测模型的可靠性开辟了一个全新的、富有前景的研究方向。

优点

1. 视角新颖，切中痛点：论文首次将“实例级预测失败”作为一个核心问题进行系统性研究，解决了现有模型“平均性能高但个体表现不稳”的实际痛点。
2. 通用性与实用性强：作为模型无关的后处理插件，PIR可以轻松地与各种现有或未来的预测模型集成，大大增强了其应用价值，而不需要对基础模型进行复杂改造。
3. 设计完备且可解释：框架设计逻辑清晰，失败识别、局部修正、全局修正三个模块各司其职、相辅相成。特别是将不确定性与预测误差挂钩的设计，为模型的修正行为提供了合理的解释。

缺点

1. 计算开销增加：该框架在原始模型的基础上增加了识别和修正的计算步骤，特别是全局检索模块，在历史数据库非常庞大时可能会引入额外的推理延迟，这在对实时性要求极高的场景下可能是一个挑战。
2. 修正效果有其边界：修正模块的有效性依赖于“有用的”上下文信息。如果局部协变量与目标变量关联性弱，或者全局历史库中不存在与当前模式相似的实例，那么修正效果可能会打折扣。
3. 对目标序列的噪声不敏感：如论文局限性部分所述，该框架主要关注由输入端变化导致的预测失败。对于由目标序列本身存在的噪声、异常值等数据质量问题，该框架并未直接处理，这为未来的研究留下了改进空间。

原文 资料 这里！