线性代数 - 3 阶方阵的行列式 可视化

线性代数 - 3 阶方阵的行列式

flyfish

只有方阵（行数与列数相等的矩阵）才有行列式。

2×2行列式表示平行四边形的面积

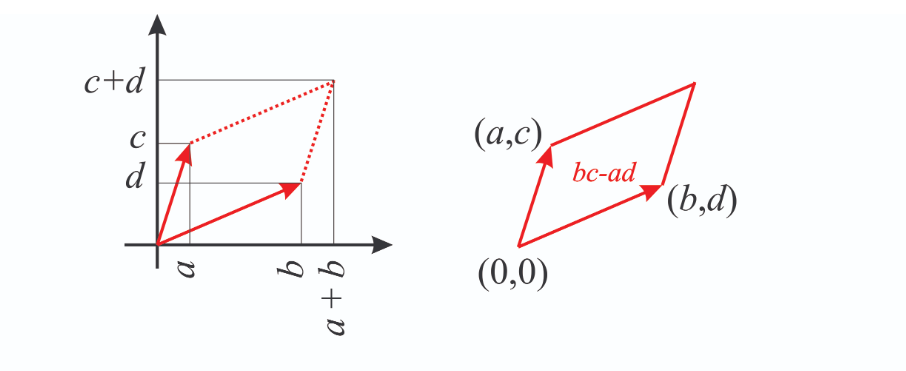
这里有详细的可视化过程

3×3行列式，其绝对值表示平行六面体的体积。

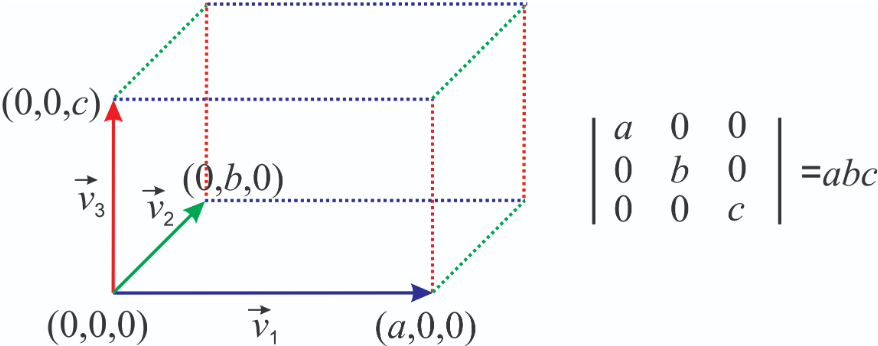
1. 长方体

三个向量 $\overrightarrow{v_1}=(a,0,0)$、$\overrightarrow{v_2}=(0,b,0)$、$\overrightarrow{v_3}=(0,0,c)$ 分别沿x、y、z轴方向延伸，张成一个长方体。
根据长方体体积公式，其体积为：
$$\text{体积}=\text{长}\times \text{宽}\times \text{高}=a\times b\times c$$

2. 矩阵与行列式部分（对角矩阵）

由这三个向量构成的3×3矩阵是对角矩阵：
$$\left|\begin{array}{ccc}a& 0& 0\\ 0& b& 0\\ 0& 0& c\end{array}\right|$$
对角矩阵的行列式等于主对角线元素的乘积，因此：
$$\text{行列式值}=a\times b\times c$$

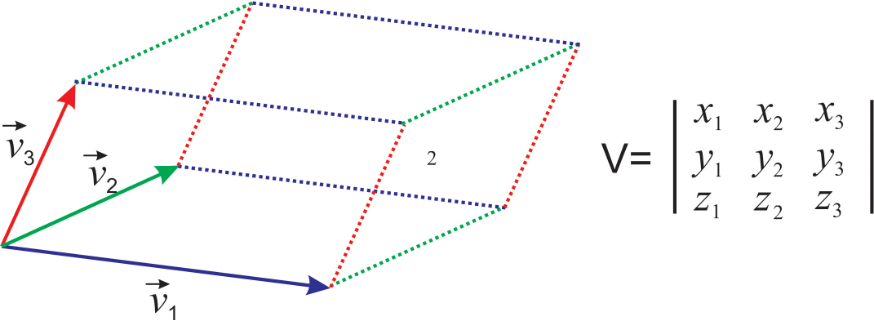
平行六面体
三个向量 $\overrightarrow{v_1}、\overrightarrow{v_2}、\overrightarrow{v_3}$ 从同一起点出发，“拉伸”后围成一个平行六面体。
行列式
若三个向量的坐标分别为 $\overrightarrow{v_1}=(x_1,y_1,z_1)$、$\overrightarrow{v_2}=(x_2,y_2,z_2)$、$\overrightarrow{v_3}=(x_3,y_3,z_3)$，则平行六面体的体积 $V$ 满足：
$$V=\left|\left|\begin{array}{ccc}{x}_1& x_2& x_3\\ y_1& y_2& y_3\\ z_1& z_2& z_3\end{array}\right|\right|$$

$$V=|h|\Vert \mathbf{a}\times \mathbf{b}\Vert =\Vert \mathbf{c}\Vert |\cos (\theta )|\Vert \mathbf{a}\times \mathbf{b}\Vert =|\mathbf{c}\cdot (\mathbf{a}\times \mathbf{b})|$$

上面式子的由来

3阶行列式

1. 基于三维向量的行列式

在三维空间${\mathbb{R}}^3$中，三个有序向量$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$的行列式定义为标量三重积：
$$\det (\mathbf{a},\mathbf{b},\mathbf{c})=\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$$
其中：
$\mathbf{b}\times \mathbf{c}$是叉积（结果为垂直于$\mathbf{b}$、$\mathbf{c}$平面的向量，模长等于$\mathbf{b}$、$\mathbf{c}$张成的平行四边形面积）；
$\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$是点积（结果为标量，其绝对值等于$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$张成的平行六面体体积）。

2. 基于3×3矩阵的行列式

若将三个向量$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$作为列向量构成3×3矩阵：
$$A=(\mathbf{a}\mathbf{b}\mathbf{c})=\left(\begin{array}{ccc}{a}_1& b_1& c_1\\ a_2& b_2& c_2\\ a_3& b_3& c_3\end{array}\right)$$
则该矩阵的行列式为：
$$\det A=\left|\begin{array}{ccc}{a}_1& b_1& c_1\\ a_2& b_2& c_2\\ a_3& b_3& c_3\end{array}\right|=\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$$

3阶行列式既可以理解为“三个三维向量的标量三重积”，也可以理解为“由这三个向量作为列（或行）构成的3×3矩阵的行列式”，其数值本质是这三个向量张成的平行六面体的体积的代数度量（符号反映定向，绝对值是体积）。

3阶行列式的“拉普拉斯展开，将3阶行列式分解为3个2阶行列式的线性组合，并通过标量三重积验证其正确性

1. 3阶行列式的按列展开（拉普拉斯展开）

3阶行列式按第一列展开：
$$\left|\begin{array}{ccc}{a}_1& b_1& c_1\\ a_2& b_2& c_2\\ a_3& b_3& c_3\end{array}\right|=a_1\left|\begin{array}{cc}{b}_2& c_2\\ b_3& c_3\end{array}\right|-a_2\left|\begin{array}{cc}{b}_1& c_1\\ b_3& c_3\end{array}\right|+a_3\left|\begin{array}{cc}{b}_1& c_1\\ b_2& c_2\end{array}\right|$$
每一项的结构：第一列的元素 × 对应的2阶余子式 × 符号（由行号+列号的奇偶性决定，第一列列号为1，故符号为$(-1{)}^{i+1}$，即$a_1$正、$a_2$负、$a_3$正）。
展开为多项式：将2阶行列式按“$mq-np$”公式展开后，得到：
$$a_1{b}_2{c}_3-a_1{b}_3{c}_2-a_2{b}_1{c}_3+a_2{b}_3{c}_1+a_3{b}_1{c}_2-a_3{b}_2{c}_1$$
这与3阶行列式的对角线法则结果完全一致。

2. 通过标量三重积验证

证明通过标量三重积（点积与叉积的结合）验证展开式的正确性：
设向量$\mathbf{a}=(a_1,a_2,a_3)$，$\mathbf{b}=(b_1,b_2,b_3)$，$\mathbf{c}=(c_1,c_2,c_3)$。
先计算叉积$\mathbf{b}\times \mathbf{c}$：
$$\mathbf{b}\times \mathbf{c}=\left(\begin{array}{c}{b}_2{c}_3-b_3{c}_2\\ b_3{c}_1-b_1{c}_3\\ b_1{c}_2-b_2{c}_1\end{array}\right)$$
再计算点积$\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$：
$$\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})=a_1(b_2{c}_3-b_3{c}_2)-a_2(b_1{c}_3-b_3{c}_1)+a_3(b_1{c}_2-b_2{c}_1)$$

展开后与行列式展开的多项式形式完全一致，从而证明了按列展开的公式是正确的。将3阶行列式分解为3个2阶行列式的线性组合（拉普拉斯展开），并通过标量三重积的代数运算验证其正确性。即通过递归，将n阶行列式分解为n个(n-1)阶行列式的组合。

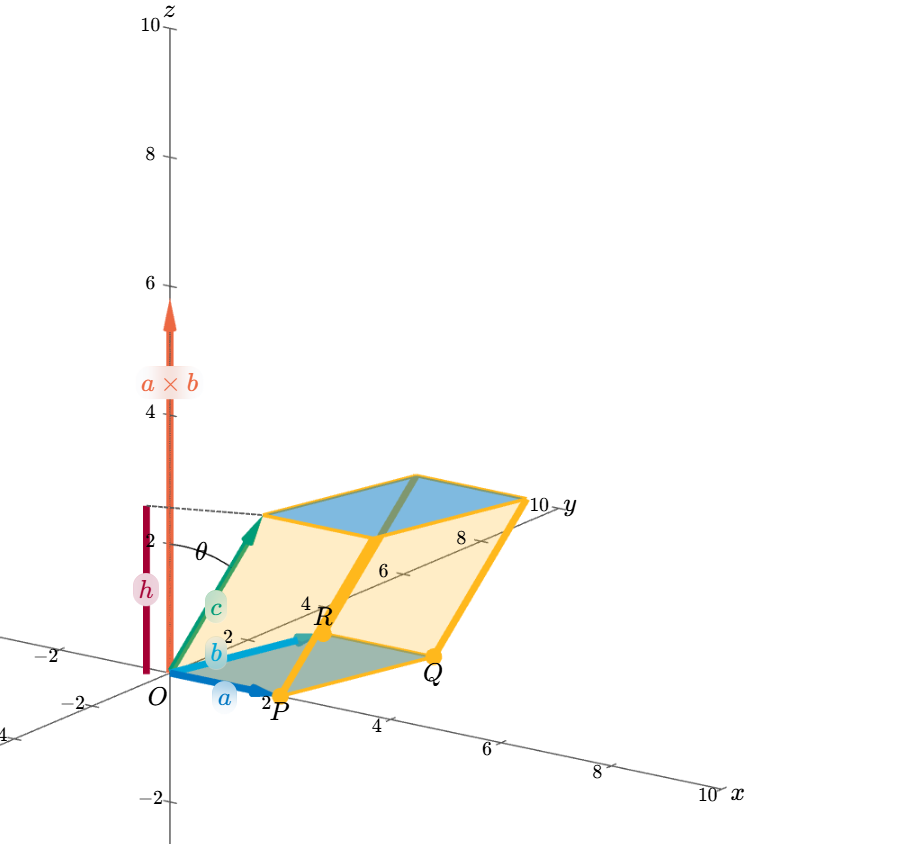
平行六面体的体积与行列式的关系，是“底面积（叉积的模长）× 高度（向量的投影）= 体积”

向量 $\vec{a}$、$\vec{b}$：在底面（X-Y平面）张成平行四边形 $OPQR$的两个边向量；
向量 $\vec{c}$：垂直于底面的“高度方向”向量；
向量 $\vec{a}\times \vec{b}$：$\vec{a}$和 $\vec{b}$的叉积向量，其方向垂直于底面，模长等于底面平行四边形的面积。

高度 $h$：向量 $\vec{c}$在底面法向（即 $\vec{a}\times \vec{b}$方向）的投影长度，计算公式为：
$$h=\Vert \vec{c}\Vert \cdot \cos (0.16\pi )=2.61$$
其中 $\Vert \vec{c}\Vert$是向量 $\vec{c}$的模长，$0.16\pi$是 $\vec{c}$与底面法向的夹角，$\cos (0.16\pi )$是投影系数。

底面积 $\mathcal{A}$：底面平行四边形 $OPQR$的面积，等于 $\vec{a}$和 $\vec{b}$叉积的模长：
$$\mathcal{A}=\Vert \vec{a}\times \vec{b}\Vert =5.82$$

体积 $\mathcal{V}$：平行六面体的体积 = 底面积 × 高度，即：
$$\mathcal{V}=h\cdot \mathcal{A}=2.61\times 5.82=15.2$$

若将 $\vec{a}、\vec{b}、\vec{c}$作为3×3矩阵的列向量，则该矩阵的行列式的绝对值就等于这个平行六面体的体积（即 $|\det (\vec{a},\vec{b},\vec{c})|=\mathcal{V}$）。而推导中，体积又被分解为“叉积的模长（底面积）× 点积的投影（高度）”。