全面且详细地解析神经网络中梯度下降(Gradient Descent, GD)的原理
1. 核心思想:下山的比喻
想象一下,你站在一座大山的某个位置,浓雾弥漫,你的目标是尽快到达山谷的最低点。你看不清全貌,但你能明确感知到当前位置的坡度。
你会怎么做?最直观的策略是:
-
环顾四周,找到最陡峭的下坡方向。
-
朝着这个方向迈出一步。
-
重复这个过程,不断地“试探-下坡”,直到你感觉到自己不再下降(到达了某个最低点)。
梯度下降就是这个过程的数学化身:
-
山: 神经网络的损失函数(Loss Function) 表面,这是一个由网络所有参数(权重和偏置)决定的高维曲面。
-
你的位置: 参数的当前值($\theta$)。
-
山谷最低点: 损失函数的最小值,此时网络参数最优,预测最准。
-
最陡峭的下坡方向: 损失函数在当前位置的负梯度(Negative Gradient)。
2. 目标:最小化损失函数
神经网络训练的唯一目标是找到一组参数(权重 $w$ 和偏置 $b$),使得网络的预测值与真实值之间的差距最小。
这个“差距”我们用一个损失函数(Loss Function)或成本函数(Cost Function),记为 $J(\theta)$ 来量化。$\theta$ 代表了网络中所有的参数。
-
例如,在回归问题中,常用的损失函数是均方误差(MSE):
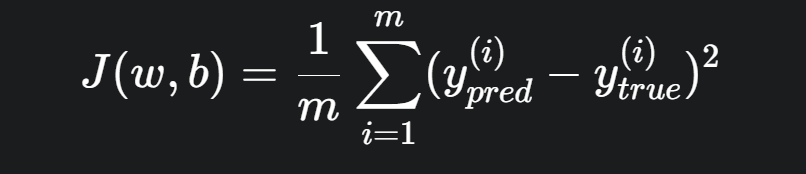

3. 关键:梯度 (Gradient)
梯度(Gradient)是一个向量,它指向函数在当前点增长最快的方向。
4. 梯度下降的更新规则
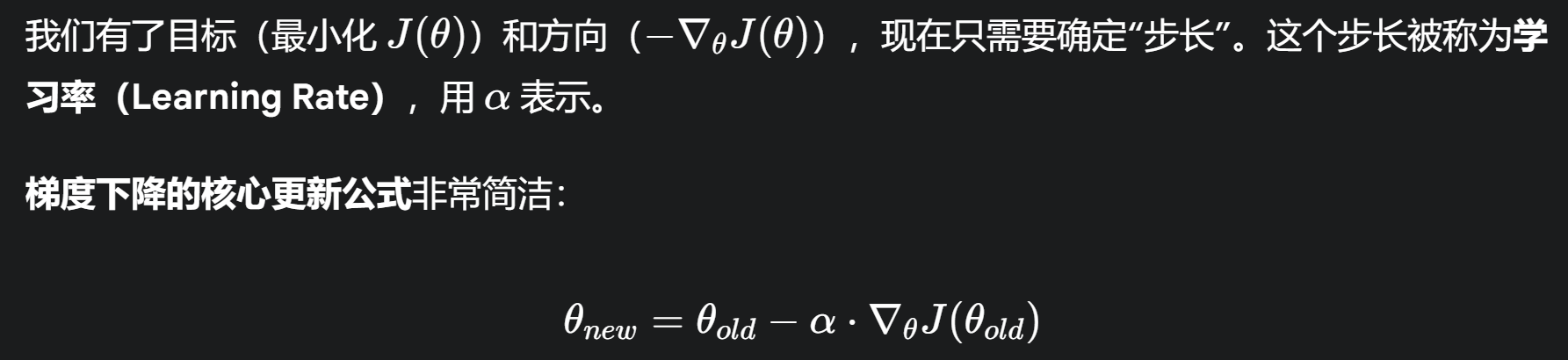
用通俗的语言解释这个迭代过程:
学习率


