当前位置：首页 > news >正文

【Algorithm】前缀和算法

news 2025/11/13 6:47:54

本篇文章主要讲解前缀和算法

1 前缀和算法的概念

1）一维前缀和

2）二维前缀和

2 总结

1 前缀和算法的概念

所谓前缀和算法，就是给你一个数组 nums，当你想要快速计算出 nums 中某一段区间元素的和的时候，比如要计算 nums 数组 [i, j] 区间元素的和，暴力解法就是从 i 下标开始，创建一个 sum 变量，记录元素的和，一直遍历到 j，显然最坏情况下就是当求的是 nums 中所有元素的和时，时间复杂度就是 O(n)。但是如果我们求 n 次 nums 所有元素的和，那么时间复杂度就会变成 O(n^2)。

这时，就可以通过前缀和算法来快速计算出 nums 数组中一段区间元素的和。在前缀和算法中，我们需要借助一个 dp 数组，dp[i] 表示的是 nums 中 [0, i] 区间内的所有元素的和。那么如果有了 dp 数组，那么 [i, j] 区间元素的和就可以写成 dp[j] - dp[i-1]，只要有这么一个 dp 数组，那就可以采用 O(1) 的时间复杂度来快速计算出 nums 中某段区间的和，这时候就会将时间复杂度变为 O(n)。

那么 dp 数组怎么填充呢？既然 dp[i] 表示的 nums 中 [0, i] 区间内元素的和，那么 dp[i-1] 就表示 nums 中 [0, i-1] 区间内元素的和，所以其实 dp[i] = dp[i - 1] + nums[i] 的，这样只要遍历一遍 nums，那么我们就可以填充完 dp 数组，进而就可以快速求出 nums 中一段区间的和了。但是在使用 dp 数组的过程中，需要注意一点，那就是如果我们求的是 nums 中 [0, i] 区间内的值呢？此时元素和就是 dp[i] - dp[-1]，这时越界了，所以为了考虑到这种边界情况，我们应该将 dp 数组开辟为 n + 1 个空间，n 为 nums 数组的元素个数，dp[1] 就代表的是 nums 数组中 [0, 0] ，也就是 nums[0] 数组的值，dp[2] 就代表 nums 数组中 [0, 1] 区间元素的和，那么 dp[0] 应该填几呢？只有当我们计算的是 [0, i] 区间的值时才会用到 dp[0]，而 [0, i] 区间元素的和存储在 dp[i + 1] 内，所以 sum = dp[i+1] - dp[0] = dp[i+1]，所以直接令 dp[0] = 0 就可以了。另外，如果 dp 增加一维，那么如果用数组下标代表数组区间，那么 [i, j] 区间的和就应该是 dp[j + 1] - dp[i] 了。总之，为了不越界，dp 数组必须增加一维，至于具体公式是什么，只要具体分析就好了。

以上就是前缀和算法的概念与基本思想，如果大家了解过动态规划算法，那么前缀和算法就是一种动态规划算法，状态标识就是 dp[i] 的含义，状态转移方程就是 dp[i] = dp[i-1] + nums[i]。前缀和算法分为一维前缀和和二维前缀和，接下来我们就通过两道题目来具体使用前缀和算法。

1）一维前缀和

链接：【模板】前缀和_牛客题霸_牛客网

题目描述：

描述

对于给定的长度为 n 的数组 {a1,a2,…,an}，我们有 m 次查询操作，每一次操作给出两个参数 l,r，你需要输出数组中第 l 到第 r 个元素之和，即 al+al+1+⋯+ar 。

输入描述：

第一行输入两个整数 n,m(1≦n,m≦10^5)，n,m(1≦n,m≦10^5) 代表数组中的元素数量、查询次数。

第二行输入 n 个整数 a1,a2,…,an(−10^9≦ai≦10^9)a1,a2,…,an(−10^9≦ai≦10^9) 代表初始数组。

此后 m 行，每行输入两个整数 l,r(1≦l≦r≦n)，l,r(1≦l≦r≦n) 代表一次查询。

输出描述：

对于每一次查询操作，在一行上输出一个整数，代表区间和。

示例1

输入：
3 2
1 2 4
1 2
2 3
输出：
3
6

题目解析：

这道题目基本上与上面所讲的前缀和算法思想相同，但还是有几个不同点的。题目中的数字是第 l 个和第 r 个数字之间所有数字的和， 0 下标就是第一个数字，1 下标就是第二个数字，所以 [l, r] 区间用下标来表示就是 [l - 1, r - 1] 区间，其他的与上面都是一样的。

注意：牛客网上的题目为 ACM 模式，也就是会给你一个 main 函数，头文件包含、输入输出等全是自己写，之前 leetcode 为核心代码模式，只实现核心函数就可以。

算法讲解：

很显然，这道题目就是采用前缀和算法了。在使用前缀和算法时，我们需要先创建一个 dp 数组，那么计算 [l, r] 区间的和的时候，因为是第 l 个数到第 r 个数，所以 sum = dp[r] - dp[l-1] 。因为出现了 dp[l - 1]，所以为了防止越界，我们需要将 dp 设置为 n + 1 维，那么预处理就是 dp[i] = dp[i - 1] + nums[i - 1]，需要注意那么几点：

（1） i 要从 1 开始，因为 dp[0] 是一个无效区间，只是为了防止越界，才多出一维的

（2）中间是加上 nums[i-1]，因为 dp[i] 是比 nums 多一维的

（3） dp[0] = 0

代码：

#include <iostream>
#include <vector>
using namespace std;int main() 
{int n, m;cin >> n >> m;vector<int> nums(n);for (int i = 0; i < n; i++) cin >> nums[i];//预处理前缀和数组//记得要开辟 n + 1 个空间vector<long long> dp(n + 1);for (int i = 1; i <= n; i++) dp[i] = dp[i-1] + nums[i-1];int l, r;for (int i = 0; i < m; i++){cin >> l >> r;cout << dp[r] - dp[l-1] << endl;}return 0;
}

2）二维前缀和

上面的都是一维前缀和，那么如果 nums 变为了一个二维数组，此时的 dp 数组也就必须跟着变为一个二维数组，那么此时的前缀和是什么呢？在一维前缀和中是计算一段区间内的值，那么当变为一个二维数组时，此时计算的就是一个 (i,j) 点到 (h, k) 点之间的所有元素的和了，(i, j) 为左上角的点，(h, k) 为右下角的点，例如：

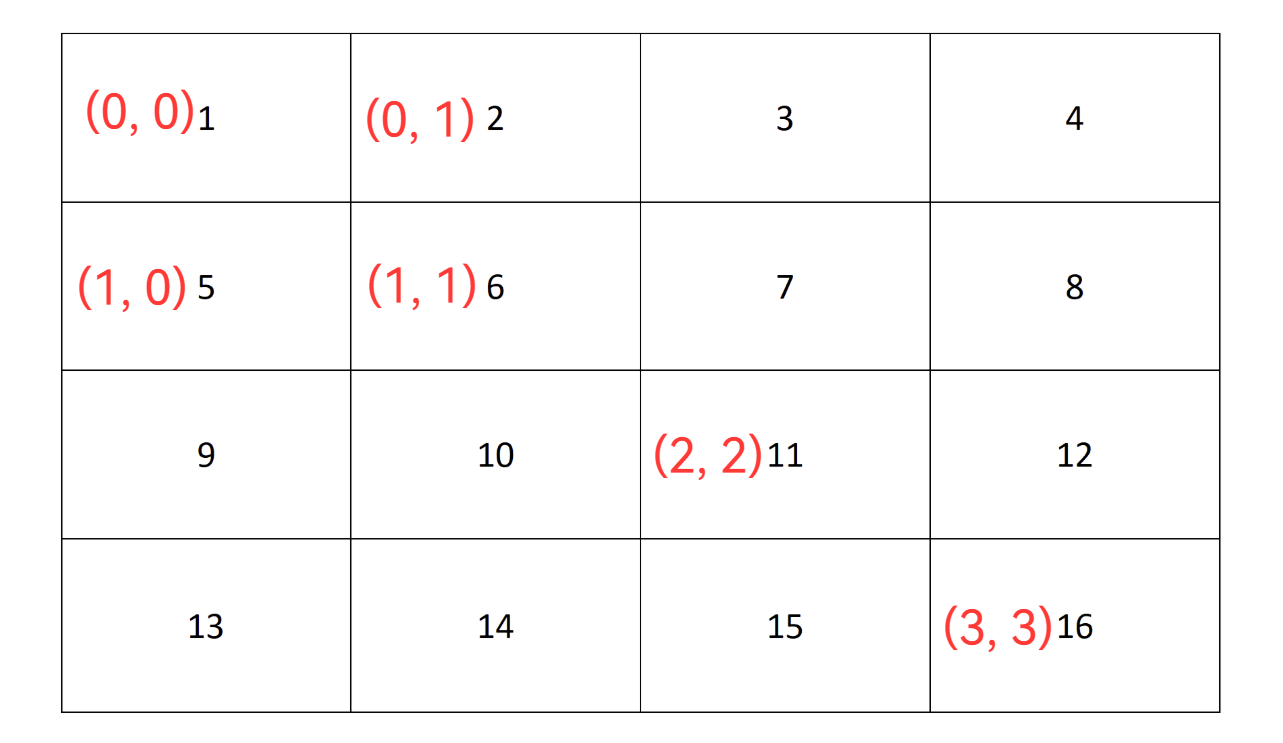
有这么一个二维数组，其中标注了一些元素的坐标，其余元素依此类推，所以说如果是 (0, 0) - (1. 1)，那么表示的就是 (0, 0)、(0, 1)、(1, 0)、(1, 1) 这四个位置元素的和。

所以仿照一维前缀和中的 dp 数组，那么二维前缀和中的 dp 数组中的 dp[i][j] 表示的就是 (0, 0) - (i, j) 这个子二维数组的元素的和，那么要求的子二维数组的和就是：

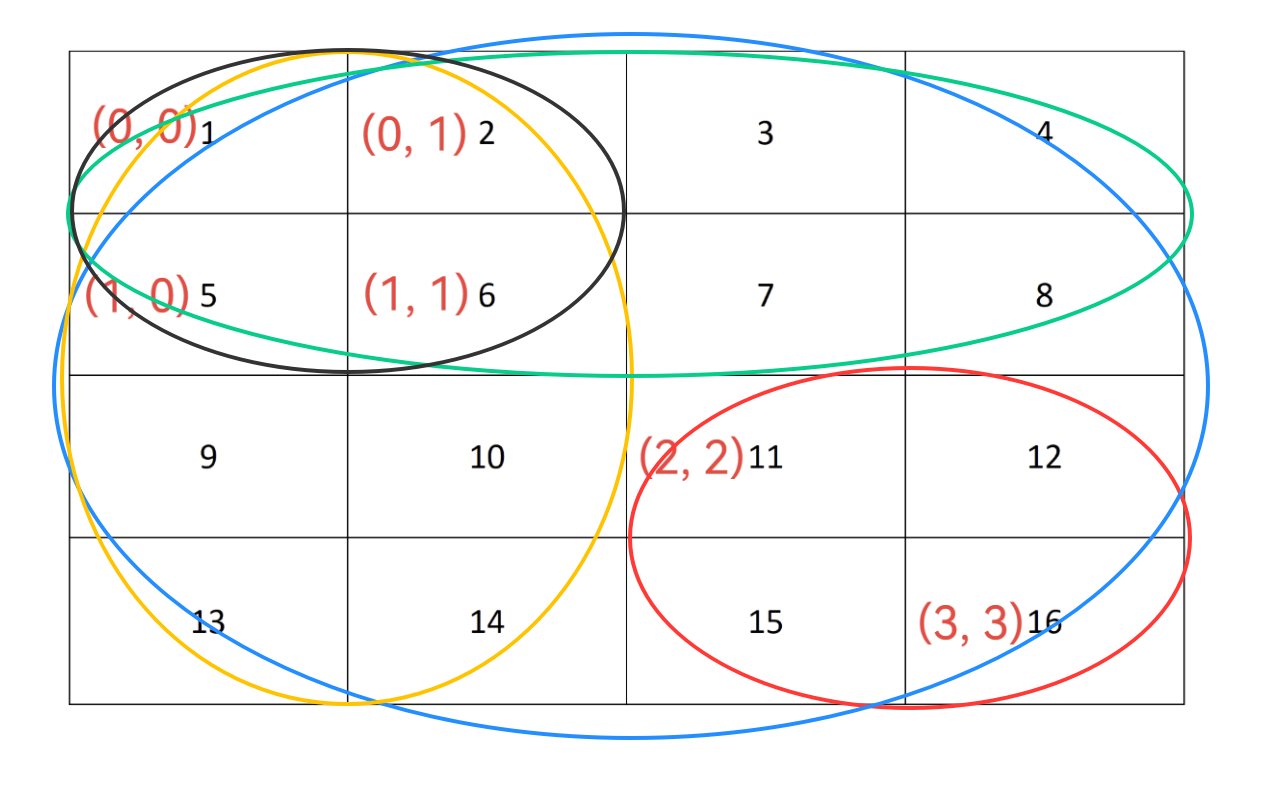
红色为要求的，那么红色 = 蓝色 - 黄色 - 绿色 + 黑色。所以如果以这种方法表示，那么 (i, j) - (h, k) 子二维数组元素和用 dp 数组表示就应该是：sum = dp[h][k] - dp[h][j - 1] - dp[i-1][k] + dp[i-1][j-1]，这样就可以利用前缀和求出子二维数组的和了。

当然与一维数组一样，我们依然要注意越界问题，如果出现了越界，那就多增加一行增加一列，初始化只要让第一行第一列全都是 0 就可以了。接下来我们通过一道题目来看一下二维前缀和。

链接：【模板】二维前缀和_牛客题霸_牛客网

题目描述：

描述

给定一个由 n 行 m 列整数组成的矩阵 {ai,j}{ai,j}（下标均从 11 开始）。
现有 q 次独立查询，第 k 次查询给定四个整数 x1,y1,x2,y2，表示左上角坐标 (x1,y1) 与右下角坐标 (x2,y2) 满足 1≦x1≦x2≦n 且 1≦y1≦y2≦m。请你计算该子矩阵中全部元素之和，记为

S(x1,y1,x2,y2)= $\sum_{i =x1}^{xn}\sum_{j = y1}^{ym}$ ai,j。你需要依次回答所有查询。

输入描述

在一行上输入三个整数 n,m,q(1≦n,m≦10^3; 1≦q≦10^5)，依次表示矩阵的行数、列数与查询次数。此后 n 行，每行输入 m 个整数 ai,1,ai,2,…,ai,m(−10^9≦ai,j≦10^9)ai,1,ai,2,…,ai,m(−10^9≦ai,j≦10^9)，表示矩阵第 i 行的元素；共计 n×m 个整数。此后 q 行，每行输入四个整数 x1,y1,x2,y2，所有变量均满足1≦x1≦x2≦n,1≦y1≦y2≦m。

输出描述

对于每一次查询，在一行上输出一个整数，表示对应子矩阵元素之和。

示例1

输入：
3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4
输出：
8
25
32

题目解析：

这道题目与上面说的是一个意思，只不过需要注意这里的左上角与右下角坐标都是从 1 开始的。

算法讲解：

很显然也是利用前缀和算法了。我们需要先预处理一个 dp 数组，这次的 dp 数组需要变成二维的，也就是 vector<vector<long long>>，这里变成 long long 主要是为了防止 int 溢出的，因为这里的 x1, y1, x2, y2 都是从 1 开始，所以我们也就需要多加一行多加一列，那么 dp[i][j] 就表示 (1, 1) 位置到 (i, j) 位置的子二维数组的和，那么为了快速填出 dp[i][j] 位置的和，我们可以想一下怎么利用前面已经求过的 dp 值来更新这个 dp[i][j] 呢？dp[i][j] 可以如图求出：

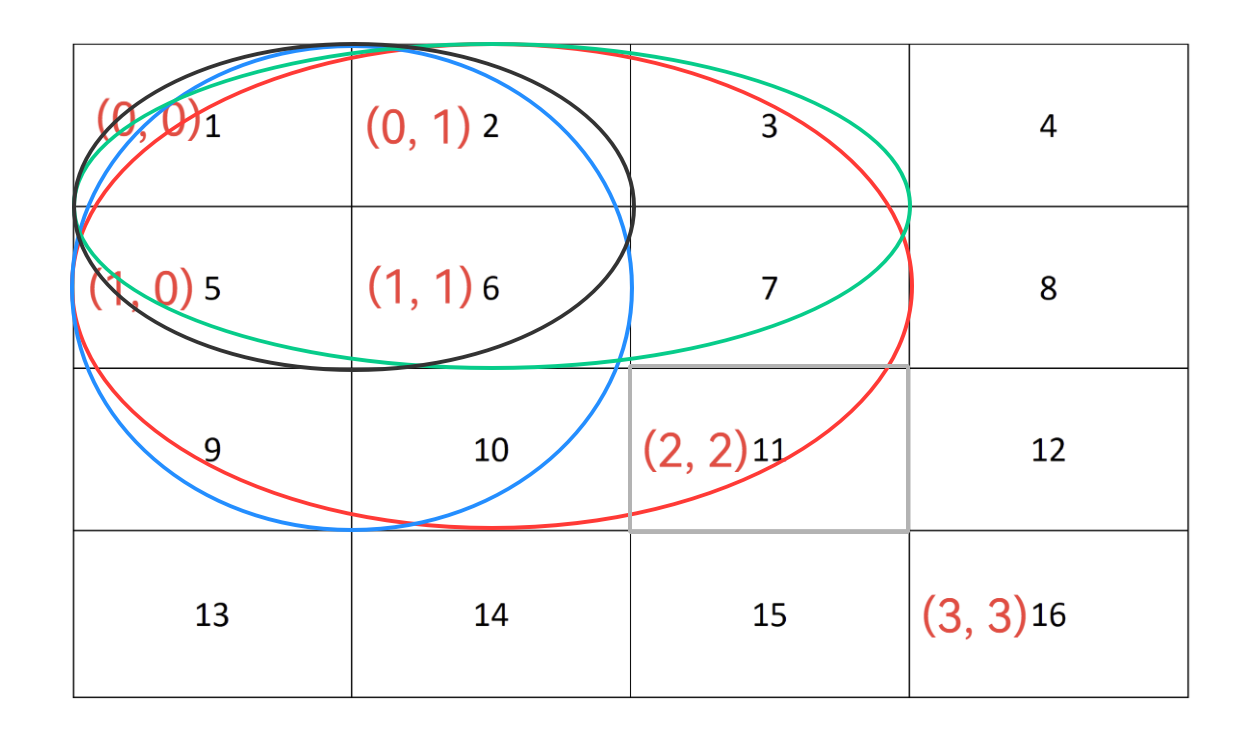
红色(dp[3][3]) = 蓝色(dp[3][2]) + 绿色(dp[2][3]) - 黑色(dp[2][2]) + 灰色(nums[2][2])（nums里面为下标，因为从 (0, 0) 开始，所以必须减 1），所以根据这个就可推断出 dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + nums[i-1][j-1]，再结合上面所讲的，即可求出结果。

代码：

#include <iostream>
#include<vector>
using namespace std;int main() 
{int n = 0, m = 0, q = 0;cin >> n >> m >> q;//1. 读入数据vector<vector<int>> arr(n+1, vector<int>(m+1));for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++)cin >> arr[i][j];//2. 处理前缀和矩阵vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));for (int i = 1;i <= n;i++)for (int j = 1;j <= m;j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];//3. 使用前缀和矩阵int x1 = 0, y1 = 0, x2 = 0, y2 = 0;while (q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x2][y1 - 1] - dp[x1-1][y2] + dp[x1 - 1][y1 - 1] << endl;}
}

2 总结

前缀和算法属于动态规划算法的一个具体实例，但是没有学过动态规划算法依然可以使用前缀和算法，当题目中让我们求出数组中某一个区间的部分元素的和时，我们就可以使用前缀和算法了。前缀和算法的核心是如何预处理 dp 数组与如何使用 dp 数组，至于那些边界情况，要不要多开一行多开一列等，具体问题具体分析就可以了。

查看全文

http://www.dtcms.com/a/601147.html