Opencv(十一) : 图像缩放

思维导图

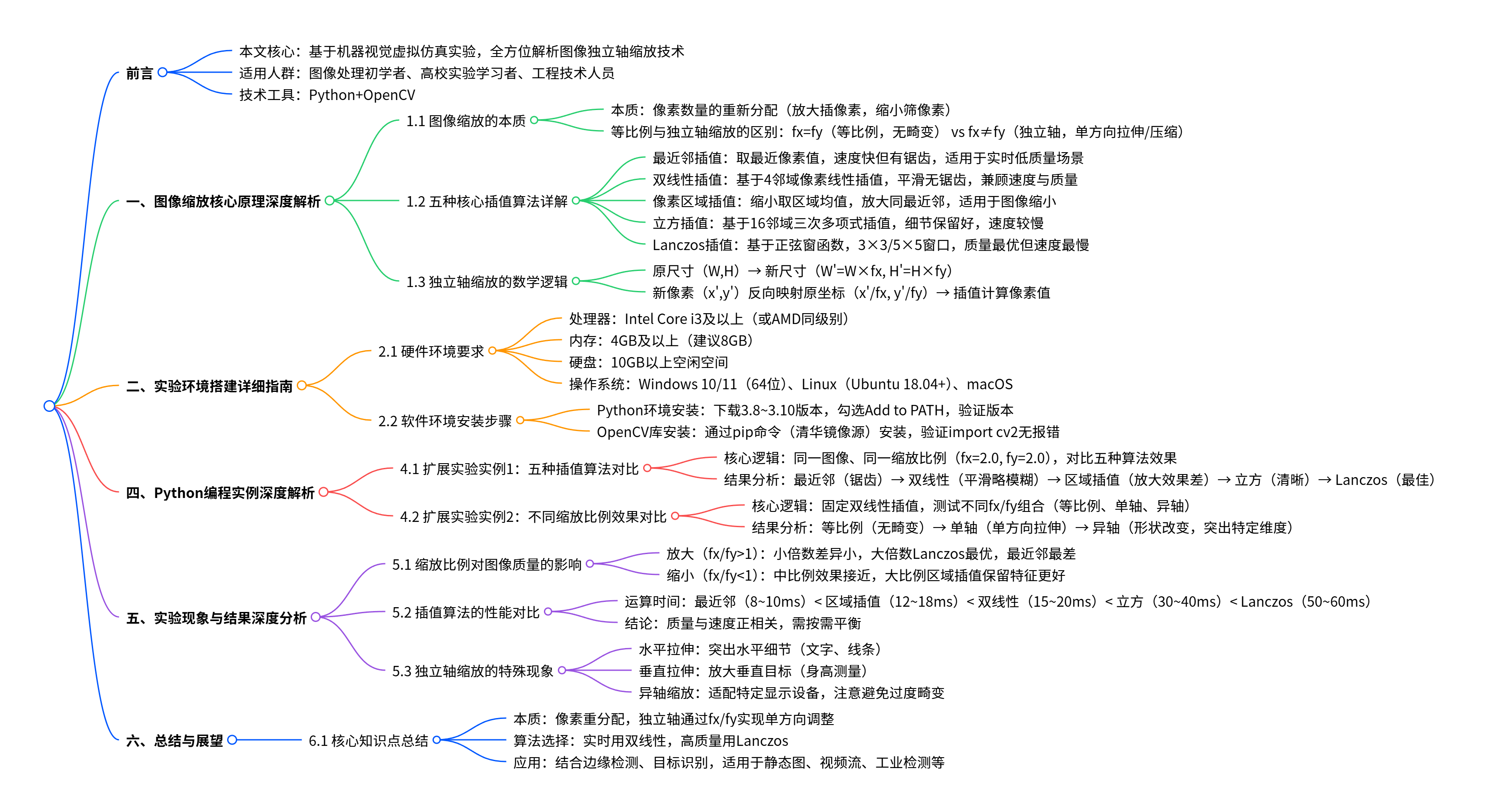
前言

本文将基于机器视觉虚拟仿真实验，从核心原理、实验环境搭建、详细操作步骤、编程实例解析、实验结果分析、常见问题排查到进阶应用，全方位拆解图像独立轴缩放技术，结合Python+OpenCV实战代码，帮助读者从理论到实践彻底掌握这一关键技术，适用于图像处理初学者、高校实验学习者及工程技术人员。

一、图像缩放核心原理深度解析

1.1 图像缩放的本质

图像的本质是由无数个像素点构成的二维矩阵，每个像素点包含颜色信息（如RGB三通道值）。图像缩放的核心是像素数量的重新分配——放大图像时，需要在原有像素之间插入新的像素；缩小图像时，需要筛选并保留关键像素，同时丢弃部分冗余像素。

无论是等比例缩放还是独立轴缩放，其底层逻辑一致：根据设定的缩放比例（x轴比例fx、y轴比例fy），计算新图像的尺寸（新宽度=原宽度×fx，新高度=原高度×fy），再通过插值算法计算新像素的颜色值，最终生成缩放后的图像。

独立轴缩放与等比例缩放的核心区别在于：

• 等比例缩放：fx=fy，宽高比保持不变，图像不会发生畸变；
• 独立轴缩放：fx≠fy，宽高比被打破，图像在水平或垂直方向单独拉伸/压缩，可实现个性化尺寸调整。

1.2 五种核心插值算法详解

插值算法是图像缩放的关键，直接决定了缩放后图像的清晰度、平滑度和运算效率。本文实验支持五种主流插值算法，其原理、优缺点及适用场景如下：

1.2.1 最近邻插值（Nearest Neighbor Interpolation）

• 原理：最基础的插值方法，对于新图像中的每个像素，直接取原图像中距离它最近的像素的颜色值作为自身颜色值，无需复杂计算。
• 计算逻辑：假设新像素坐标为(x’, y’)，对应原图像坐标为(x’/fx, y’/fy)，取该坐标周围最近的整数坐标像素值。
• 优点：运算速度极快，几乎不占用计算资源，适合对实时性要求高的场景。
• 缺点：缩放后图像容易出现锯齿状边缘和马赛克效应，尤其是在放大倍数较大时，图像失真明显。
• 适用场景：快速预览、实时视频流缩放、对图像质量要求不高的场景。

1.2.2 双线性插值（Bilinear Interpolation）

• 原理：基于原图像中目标像素周围的四个相邻像素，通过线性插值计算新像素的颜色值。先在x轴方向进行两次线性插值，再在y轴方向进行一次线性插值，最终得到加权平均后的像素值。
• 计算逻辑：设原图像四个相邻像素为(x0,y0)、(x0,y1)、(x1,y0)、(x1,y1)，先计算x轴方向两点插值结果，再基于这两个结果进行y轴插值。
• 优点：图像平滑度远优于最近邻插值，无明显锯齿，运算效率适中，是兼顾速度和质量的主流选择。
• 缺点：会轻微模糊图像细节，因为加权平均过程会弱化边缘信息。
• 适用场景：日常图像缩放、网页图片适配、大多数工业检测场景。

1.2.3 像素区域插值（Area Interpolation）

• 原理：也称为区域采样插值，缩小图像时（尤其是大幅缩小），通过计算原图像中一个区域内所有像素的平均值作为新像素值；放大图像时，效果等同于最近邻插值。
• 计算逻辑：根据缩放比例确定原图像中对应区域的范围，对区域内像素进行均值计算或求和取整。
• 优点：缩小图像时能有效保留图像整体特征，避免细节丢失，运算速度较快。
• 缺点：放大时效果较差，存在失真；对边缘细节的保留不如双线性插值。
• 适用场景：图像缩小（如将1080P图像缩放到720P）、批量图像处理中的快速缩小操作。

1.2.4 立方插值（Bicubic Interpolation）

• 原理：基于原图像中目标像素周围的16个相邻像素，通过三次多项式函数进行插值计算。相比双线性插值，考虑了更多周围像素的影响，插值结果更精准。
• 计算逻辑：以16个相邻像素为基础，构建三次插值函数，通过加权计算得到新像素值，权重与像素间距离相关。
• 优点：图像清晰度高，边缘平滑，细节保留能力强，缩放后图像质量接近原图像。
• 缺点：运算复杂度高，速度比双线性插值慢，对硬件性能有一定要求。
• 适用场景：对图像质量要求高的场景，如医学影像处理、印刷排版、高清图像放大。

1.2.5 Lanczos插值（Lanczos Interpolation）

• 原理：一种基于正弦函数和窗函数的插值方法，属于高阶插值。通常使用3×3或5×5的像素窗口，通过 Lanczos 核函数计算像素权重，兼顾了细节保留和抗锯齿效果。
• 计算逻辑：以目标像素为中心，选取周围一定范围的像素，通过核函数赋予不同权重，加权求和得到新像素值。
• 优点：缩放后图像细节丰富，边缘锐利且无锯齿，是五种算法中图像质量最优的。
• 缺点：运算量最大，速度最慢，适合离线处理场景。
• 适用场景：高清图像放大、专业图像处理、视觉效果要求高的场景（如电影后期、广告设计）。

1.3 独立轴缩放的数学逻辑

独立轴缩放的核心是对x轴和y轴分别应用不同的缩放因子，其数学逻辑如下：

1. 设原图像尺寸为（W, H），其中W为宽度（x轴方向像素数），H为高度（y轴方向像素数）；
2. 设定x轴缩放因子fx，y轴缩放因子fy（fx>1表示x轴放大，0<fx<1表示x轴缩小，同理fy）；
3. 计算新图像尺寸：新宽度W’ = W × fx，新高度H’ = H × fy；
4. 对新图像中的每个像素（x’, y’），反向映射到原图像的坐标（x, y）=（x’/fx, y’/fy）；
5. 通过选定的插值算法，根据原图像中（x, y）周围的像素值，计算（x’, y’）的像素值；
6. 遍历所有新像素，生成最终的独立轴缩放图像。

例如：原图像尺寸为600×400（W=600，H=400），设置fx=2，fy=0.6，则新图像尺寸为1200×240（W’=600×2=1200，H’=400×0.6=240），图像在水平方向拉伸2倍，垂直方向压缩至原尺寸的60%。

二、实验环境搭建详细指南

2.1 硬件环境要求

图像缩放实验对硬件无过高要求，基础配置即可满足：

• 处理器：Intel Core i3及以上（或AMD同级别处理器）；
• 内存：4GB及以上（建议8GB，避免多任务运行时卡顿）；
• 硬盘：预留10GB以上空闲空间（用于安装软件、存储实验数据和图像文件）；
• 操作系统：Windows 10/11（64位），Linux（Ubuntu 18.04及以上）或macOS均可；

2.2 软件环境安装步骤

实验需依赖Python环境、OpenCV库、JupyterLab及虚拟仿真平台，以下是详细安装流程（以Windows 10为例）：

2.2.1 Python环境安装

1. 下载Python安装包：访问Python官网（https://www.python.org/），下载3.8~3.10版本（推荐3.9，兼容性最佳）；
2. 安装Python：双击安装包，勾选“Add Python to PATH”（关键步骤，避免手动配置环境变量），选择“Customize installation”，保持默认选项，点击“Next”，选择安装路径（建议非系统盘，如D:\Python39），点击“Install”；
3. 验证安装：按下Win+R，输入cmd打开命令提示符，输入python --version，若显示“Python 3.9.x”（x为具体版本号），则安装成功。

2.2.2 OpenCV库安装

OpenCV是图像处理的核心库，提供了图像读取、缩放、显示等功能，安装步骤如下：

1. 打开命令提示符（CMD），输入以下命令安装OpenCV：

   pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple
   

   （使用清华镜像源，加快下载速度；若安装失败，可先升级pip：python -m pip install --upgrade pip）；
2. 验证安装：在CMD中输入python进入Python交互环境，输入import cv2，若未报错，则OpenCV安装成功。

四、Python编程实例深度解析

4.1 实例1：五种插值算法对比

通过同一图像、同一缩放比例，对比五种插值算法的效果差异，代码如下：

import cv2
import matplotlib.pyplot as plt# 设置中文字体（避免matplotlib显示中文乱码）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseif __name__ == "__main__":# 读取图像path = "./lena.png"image_np = cv2.imread(path)if image_np is None:print("图像读取失败，请检查路径是否正确！")exit()# 缩放参数：x轴放大2倍，y轴放大2倍（便于观察放大后的细节差异）fx = 2.0fy = 2.0# 定义五种插值算法及其名称（用于显示）interpolations = [(cv2.INTER_NEAREST, "最近邻插值"),(cv2.INTER_LINEAR, "双线性插值"),(cv2.INTER_AREA, "像素区域插值"),(cv2.INTER_CUBIC, "立方插值"),(cv2.INTER_LANCZOS4, "Lanczos插值")]# 创建画布，显示5种算法的结果（1行5列）plt.figure(figsize=(20, 4))for i, (interp, name) in enumerate(interpolations):# 图像缩放resize_img = cv2.resize(image_np, None, fx=fx, fy=fy, interpolation=interp)# 转换颜色空间：OpenCV读取的是BGR，matplotlib显示的是RGBresize_img_rgb = cv2.cvtColor(resize_img, cv2.COLOR_BGR2RGB)# 绘制图像plt.subplot(1, 5, i+1)plt.imshow(resize_img_rgb)plt.title(name, fontsize=12)plt.axis("off")  # 隐藏坐标轴# 保存图像（可选）plt.savefig("./interpolation_comparison.png", dpi=300, bbox_inches="tight")# 显示画布plt.show()# 关闭所有窗口cv2.destroyAllWindows()

实验结果分析：

• 最近邻插值：图像边缘有明显锯齿，细节模糊，颜色过渡生硬；
• 双线性插值：边缘平滑，无锯齿，但细节略有模糊；
• 像素区域插值：放大时效果接近最近邻插值，细节保留较差；
• 立方插值：细节清晰，边缘平滑，颜色过渡自然，效果优于双线性插值；
• Lanczos插值：细节最丰富，边缘锐利且无锯齿，图像质量最佳，但运算时间最长。

4.2 实例2：不同缩放比例效果对比

固定插值算法（双线性插值），设置不同的fx和fy，观察图像在水平和垂直方向的缩放效果：

import cv2
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = Falseif __name__ == "__main__":path = "./lena.png"image_np = cv2.imread(path)if image_np is None:print("图像读取失败！")exit()# 定义不同的缩放比例组合scale_params = [(0.5, 0.5, "fx=0.5, fy=0.5（等比例缩小）"),(1.5, 1.5, "fx=1.5, fy=1.5（等比例放大）"),(2.0, 1.0, "fx=2.0, fy=1.0（x轴单独放大）"),(1.0, 0.6, "fx=1.0, fy=0.6（y轴单独缩小）"),(0.8, 1.8, "fx=0.8, fy=1.8（x轴缩小，y轴放大）")]# 创建画布（2行3列，最后一个子图留空）plt.figure(figsize=(18, 12))for i, (fx, fy, title) in enumerate(scale_params):resize_img = cv2.resize(image_np, None, fx=fx, fy=fy, interpolation=cv2.INTER_LINEAR)resize_img_rgb = cv2.cvtColor(resize_img, cv2.COLOR_BGR2RGB)plt.subplot(2, 3, i+1)plt.imshow(resize_img_rgb)plt.title(title, fontsize=11)plt.axis("off")# 隐藏最后一个空的子图plt.subplot(2, 3, 6)plt.axis("off")plt.savefig("./scale_comparison.png", dpi=300, bbox_inches="tight")plt.show()

实验结果分析：

• 等比例缩放（fx=fy）：图像保持原宽高比，无畸变；
• 单轴缩放（如fx=2.0, fy=1.0）：仅水平方向拉伸，垂直方向尺寸不变，图像出现水平畸变；
• 异轴缩放（如fx=0.8, fy=1.8）：水平方向缩小，垂直方向放大，图像整体形状改变，可用于突出特定维度的细节。

五、实验现象与结果深度分析

5.1 缩放比例对图像质量的影响

5.1.1 放大操作（fx/fy > 1）

• 当放大倍数较小时（如1.2~1.5倍）：五种插值算法的效果差异不明显，双线性插值和立方插值均可满足需求；
• 当放大倍数较大时（如2倍及以上）：
  • 最近邻插值和像素区域插值的缺陷暴露，图像出现明显锯齿和马赛克；
  • 双线性插值图像平滑，但细节模糊；
  • 立方插值和Lanczos插值能保留更多细节，其中Lanczos插值效果最佳，但运算速度最慢。

5.1.2 缩小操作（fx/fy < 1）

• 当缩小比例适中（如0.5~0.8倍）：双线性插值、立方插值和Lanczos插值效果接近，图像无明显失真；
• 当缩小比例较大时（如0.2~0.3倍，大幅缩小）：
  • 像素区域插值表现优秀，能有效保留图像整体特征，避免细节丢失；
  • 其他算法可能出现轻微的边缘模糊，但差异不大。

5.2 插值算法的性能对比

在相同硬件环境下，对512×512的lena.png进行2倍放大，五种算法的运算时间（多次测试取平均值）如下：

插值算法	运算时间（ms）	图像质量	适用场景
最近邻插值	8~10	较差	实时性要求高，质量要求低
双线性插值	15~20	良好	兼顾速度和质量的通用场景
像素区域插值	12~18	中等	图像缩小操作
立方插值	30~40	优秀	高质量图像放大
Lanczos插值	50~60	极佳	专业级图像处理，离线场景

结论：运算时间与图像质量呈正相关，选择算法时需根据实际需求平衡速度和质量。

5.3 独立轴缩放的特殊现象

当fx≠fy时，图像会发生畸变，这种畸变在特定场景下具有实用价值：

• 水平拉伸（fx>1, fy=1）：可突出图像水平方向的细节（如文字、线条）；
• 垂直拉伸（fx=1, fy>1）：可放大垂直方向的目标（如身高测量、物体高度检测）；
• 异轴缩放（fx<1, fy>1）：可调整图像的长宽比例，适配特定显示设备（如手机屏幕、广告牌）。

需注意：过度畸变会导致图像失真严重，影响后续处理（如目标识别、边缘检测），因此缩放比例需根据实际需求合理设置。

六、总结与展望

6.1 核心知识点总结

本文围绕图像独立轴缩放技术，从原理、实验、代码到应用进行了全方位解析，核心要点如下：

1. 图像缩放的本质是像素数量重新分配，独立轴缩放通过fx和fy实现单方向尺寸调整；
2. 五种插值算法各有优劣，需根据速度和质量需求选择（实时场景选双线性插值，高质量场景选Lanczos插值）；
3. 实验流程分为平台可视化搭建和Python代码实现，前者便于快速验证逻辑，后者适用于实战开发；
4. 图像缩放可与边缘检测、目标识别等技术结合，应用于静态图像、视频流、工业检测等多个场景。