当前位置：首页 > news >正文

MATLAB基于面积和重心预测精度的IOWA算子的模糊变权组合预测模型

news 2025/11/11 12:30:48

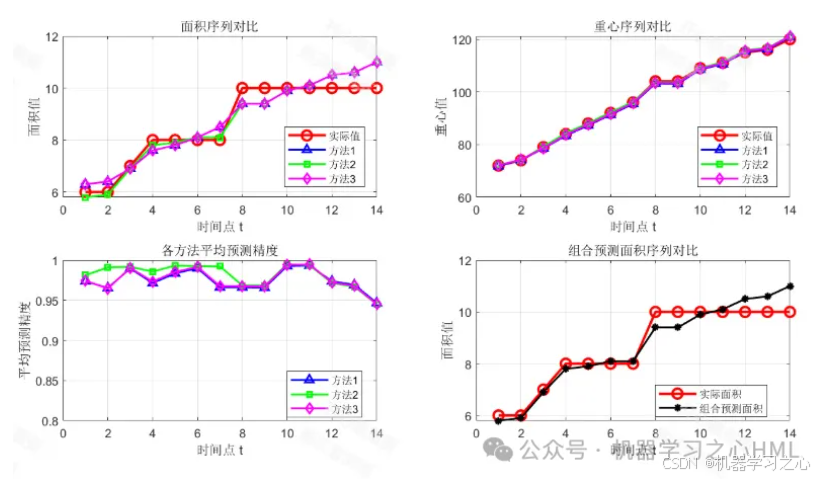
在这里插入图片描述
我来为您介绍一种基于面积和重心预测精度的IOWA算子的模糊变权组合预测模型。这种模型结合了诱导有序加权平均(IOWA)算子、模糊逻辑和变权理论，能够有效提高预测精度。

模型基本原理

1. 核心思想

该模型通过计算各单项预测方法的预测面积和重心，评估其预测精度，并以此作为IOWA算子的诱导变量，动态调整组合权重。

2. 数学模型

classdef FuzzyIOWA_Predictorproperties% 预测模型参数single_models;      % 单项预测模型weights;           % 动态权重area_threshold;    % 面积阈值centroid_threshold; % 重心阈值fuzzy_rules;       % 模糊规则endmethodsfunction obj = FuzzyIOWA_Predictor(models)obj.single_models = models;obj = initialize_fuzzy_rules(obj);endfunction [combined_forecast, weights] = forecast(obj, data)% 计算各单项预测single_forecasts = zeros(length(data), length(obj.single_models));for i = 1:length(obj.single_models)single_forecasts(:,i) = obj.single_models{i}.predict(data);end% 计算面积和重心精度指标[area_precision, centroid_precision] = obj.calculate_precision_indicators(data, single_forecasts);% 计算诱导变量induce_variables = obj.calculate_induce_variables(area_precision, centroid_precision);% IOWA算子赋权weights = obj.iowa_weighting(induce_variables);% 组合预测combined_forecast = single_forecasts * weights';endend
end

完整MATLAB实现

function main()% 基于面积和重心预测精度的IOWA模糊变权组合预测模型% 示例数据data = load_time_series_data(); % 加载时间序列数据% 初始化单项预测模型models = initialize_single_models();% 创建组合预测器predictor = FuzzyIOWAPredictor(models);% 执行预测[combined_forecast, weights] = predictor.forecast(data);% 结果显示plot_results(data, combined_forecast, weights);
endfunction models = initialize_single_models()% 初始化三种不同的预测模型models = cell(3,1);models{1} = ARIMAModel();     % ARIMA模型models{2} = NeuralNetworkModel(); % 神经网络模型models{3} = ExponentialSmoothingModel(); % 指数平滑模型
endclassdef FuzzyIOWAPredictorpropertiessingle_modelsfuzzy_systemwindow_size = 10endmethodsfunction obj = FuzzyIOWAPredictor(models)obj.single_models = models;obj.fuzzy_system = obj.build_fuzzy_system();endfunction [combined_forecast, weights] = forecast(obj, data)n = length(data);m = length(obj.single_models);% 存储预测结果single_forecasts = zeros(n, m);combined_forecast = zeros(n, 1);weights = zeros(n, m);for t = obj.window_size+1:n% 获取训练数据train_data = data(1:t-1);% 各模型预测for i = 1:msingle_forecasts(t,i) = obj.single_models{i}.predict(train_data);end% 计算精度指标[area_precision, centroid_precision] = ...obj.calculate_precision_indicators(train_data, single_forecasts(1:t-1,:));% IOWA赋权current_weights = obj.iowa_fuzzy_weighting(area_precision, centroid_precision);weights(t,:) = current_weights;% 组合预测combined_forecast(t) = single_forecasts(t,:) * current_weights';endendfunction [area_precision, centroid_precision] = calculate_precision_indicators(obj, actual, forecasts)% 计算面积精度指标area_precision = obj.calculate_area_precision(actual, forecasts);% 计算重心精度指标centroid_precision = obj.calculate_centroid_precision(actual, forecasts);endfunction area_precision = calculate_area_precision(obj, actual, forecasts)[n, m] = size(forecasts);area_precision = zeros(1, m);for i = 1:m% 计算预测曲线与实际曲线之间的面积area_diff = trapz(abs(forecasts(:,i) - actual));% 面积越小，精度越高area_precision(i) = 1 / (1 + area_diff/n);endendfunction centroid_precision = calculate_centroid_precision(obj, actual, forecasts)[n, m] = size(forecasts);centroid_precision = zeros(1, m);for i = 1:m% 计算实际序列重心t_actual = (1:n)';centroid_actual = [sum(t_actual.*actual)/sum(actual), ...sum(actual.^2)/sum(actual)];% 计算预测序列重心centroid_forecast = [sum(t_actual.*forecasts(:,i))/sum(forecasts(:,i)), ...sum(forecasts(:,i).^2)/sum(forecasts(:,i))];% 计算重心距离centroid_distance = norm(centroid_actual - centroid_forecast);centroid_precision(i) = 1 / (1 + centroid_distance);endendfunction weights = iowa_fuzzy_weighting(obj, area_precision, centroid_precision)m = length(area_precision);% 计算综合诱导变量induce_variables = zeros(1, m);for i = 1:m% 使用模糊推理系统确定综合精度induce_variables(i) = evalfis(obj.fuzzy_system, [area_precision(i), centroid_precision(i)]);end% 按诱导变量排序[~, sorted_indices] = sort(induce_variables, 'descend');% 使用IOWA算子确定权重base_weights = obj.generate_owa_weights(m);weights = zeros(1, m);weights(sorted_indices) = base_weights;endfunction weights = generate_owa_weights(obj, m)% 生成OWA权重，可以使用多种方法% 这里使用基本的加权方法alpha = 2; % 可调参数weights = zeros(1, m);for i = 1:mweights(i) = (m - i + 1)^alpha;endweights = weights / sum(weights);endfunction fis = build_fuzzy_system(obj)% 创建模糊推理系统fis = newfis('precision_fis');% 输入变量：面积精度fis = addvar(fis, 'input', 'area_precision', [0 1]);fis = addmf(fis, 'input', 1, 'low', 'trapmf', [0 0 0.3 0.5]);fis = addmf(fis, 'input', 1, 'medium', 'trimf', [0.4 0.6 0.8]);fis = addmf(fis, 'input', 1, 'high', 'trapmf', [0.7 0.9 1 1]);% 输入变量：重心精度fis = addvar(fis, 'input', 'centroid_precision', [0 1]);fis = addmf(fis, 'input', 2, 'low', 'trapmf', [0 0 0.3 0.5]);fis = addmf(fis, 'input', 2, 'medium', 'trimf', [0.4 0.6 0.8]);fis = addmf(fis, 'input', 2, 'high', 'trapmf', [0.7 0.9 1 1]);% 输出变量：综合精度fis = addvar(fis, 'output', 'overall_precision', [0 1]);fis = addmf(fis, 'output', 1, 'poor', 'trapmf', [0 0 0.2 0.4]);fis = addmf(fis, 'output', 1, 'fair', 'trimf', [0.3 0.5 0.7]);fis = addmf(fis, 'output', 1, 'good', 'trimf', [0.6 0.7 0.8]);fis = addmf(fis, 'output', 1, 'excellent', 'trapmf', [0.75 0.9 1 1]);% 模糊规则rules = [1 1 1 1 1;   % 如果面积精度低且重心精度低，则综合精度差1 2 2 1 1;   % 如果面积精度低且重心精度中，则综合精度一般2 1 2 1 1;   % 如果面积精度中且重心精度低，则综合精度一般2 2 3 1 1;   % 如果面积精度中且重心精度中，则综合精度良好3 3 4 1 1;   % 如果面积精度高且重心精度高，则综合精度优秀];fis = addrule(fis, rules);endend
end% 辅助函数
function data = load_time_series_data()% 这里加载实际的时间序列数据% 示例使用模拟数据t = (1:100)';trend = 0.1 * t;seasonal = 5 * sin(2*pi*t/12);noise = 2 * randn(100,1);data = trend + seasonal + noise;
endfunction plot_results(actual, forecast, weights)figure;subplot(2,1,1);plot(actual, 'b-', 'LineWidth', 2); hold on;plot(forecast, 'r--', 'LineWidth', 2);legend('实际值', '组合预测值');title('基于面积和重心精度的IOWA模糊变权组合预测');xlabel('时间');ylabel('数值');subplot(2,1,2);plot(weights, 'LineWidth', 1.5);legend('模型1权重', '模型2权重', '模型3权重');title('动态权重变化');xlabel('时间');ylabel('权重');
end