当前位置：首页 > news >正文

基础算法精讲 09|递归|操作型|计算型

news 2025/11/11 12:22:55

递归

递归的思想

递归二字要分开理解。

递。把原问题一层层的传递给下一层。每一层都会给出答案的几分之一。写代码的逻辑就是，找到最小逻辑单元，处理特殊情况或者完成题目中的要求。
归。到了最后一层，会给出一个最终答案（几分之一的最后一个）

计算二叉树中所有结点个数

操作型（回溯）

写出前序遍历，遍历各个结点的逻辑就可以了。
与计算型相比，不用分类讨论结点的所有情况。但需要处理好回溯

class Solution{int n=0;void dfs(BiTree* p){if(p==nullptr)return;n++;	dfs(p->left);dfs(p->right);	}
};

计算型（分类讨论+抽象）

对根节点进行分类讨论，然后抽象左子树和右子树。

p是空结点
p左空右不空
p左不空右空
p左不空右不空
但是p的左右空不空并不会有什么影响
所以应该只分以下两类

p是空结点
其他

计算二叉树中所有叶子结点个数

操作型

写出前序遍历的各个结点的逻辑

class Solution{int n=0;void dfs(BiTree* p){	if(p==nullptr)return;//叶子结点时才n++if(p->left==nullptr && p->right==nullptr)n++;dfs(p->left);dfs(p->right);	}
};

计算型（p的分类讨论）

p是单节点
其他（包含【 p左空右不空】【p左不空右空】【p左不空右不空】）

计算二叉树中所有双分支的结点个数

操作型

class Solution{int n=0;void dfs(BiTree* p){	if(p==nullptr)return;//叶子结点时才n++if(p->left！=nullptr && p->right！=nullptr)n++;dfs(p->left);dfs(p->right);	}
};

计算型

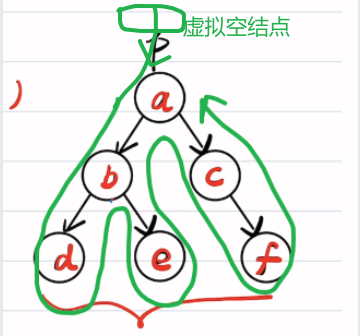
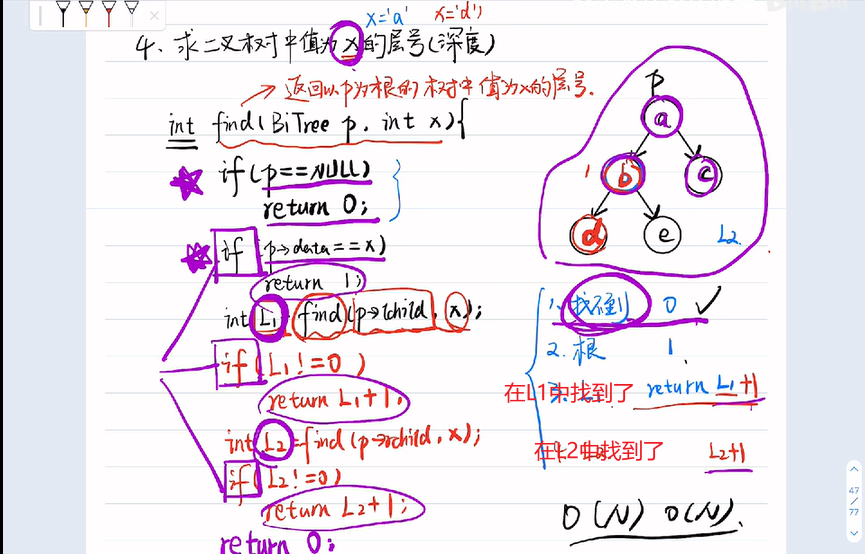
在这里插入图片描述

求二叉树中值是x的层号

class Solution{int depth=0;void dfs(BiTree* p){	if(p==nullptr)return;//找到这个值了if(p->val== x)printf("找到了%d"，depth);depth++;dfs(p->left);dfs(p->right);	depth--;}
};

计算型

p分类讨论

在这里插入图片描述

104. 二叉树的最大深度

操作型

class Solution {
public:int depth = 0;  // 当前深度int res = 0;  // 最大深度int maxDepth(TreeNode* root) {traverse(root);return res;}void traverse(TreeNode* root) {if (root == nullptr) return;depth++;  // 进入节点，深度+1res = max(res, depth);  // 更新最大深度traverse(root->left);traverse(root->right);depth--;  // 离开节点，深度-1（回溯）}

计算型

p是空结点
只有p一个结点
p左空右不空
p左不空右空
p左不空右不空

    //这个函数是用来计算根节点为子树的最大深度int maxDepth(TreeNode* root){//if(root==nullptr)return 0;if(root->left==nullptr&&root->right==nullptr)return 1;else if(root->left == nullptr&&root->right!=nullptr)return maxDepth(root->right)+1;else if(root->left != nullptr&&root->right==nullptr)return maxDepth(root->left)+1;elsereturn max(maxDepth(root->left),maxDepth(root->right))+1;}

优化

p空
else 中就包含了只有p一个结点/p左空右不空/p左不空右空/p左不空右不空。这些逻辑

int maxDepth(TreeNode* root){//if(root==nullptr)return 0;return max(maxDepth(root->left),maxDepth(root->right))+1;                }

111. 二叉树的最小深度

操作型

顺着前序遍历的遍历走，一个结点一个结点的分析可能碰到的情况。

class Solution {
public:int depth=0;int res=INT_MAX;void dfs(TreeNode* t){if(t==nullptr){return;}depth++;if(t->left==nullptr&&t->right==nullptr)res=min(res,depth);dfs(t->left);dfs(t->right);depth--;}int minDepth(TreeNode* root) {dfs(root);      return root==nullptr?0:res;}
};

计算型

对p进行分类讨论。

class Solution {
public://求以root为根的树的最小深度int minDepth(TreeNode* root) {if(root==nullptr)return 0;//对p进行分类讨论喽if(root->left!=nullptr&& root->right==nullptr)//求以root->left为根的子树的最小深度return minDepth(root->left)+1;if(root->left==nullptr&& root->right!=nullptr)//求以root->right为根的子树的最小深度return minDepth(root->right)+1;int l = minDepth(root->left);int r = minDepth(root->right);return min(l,r)+1;}
};

404. 左叶子之和

操作型

顺着前序遍历的遍历走，一个结点一个结点的分析可能碰到的情况。

class Solution {
public:int res=0;void tra(TreeNode* t){if(t==nullptr)return;//记住是操作型，不需要返回值。对res进行操作即可。//如果该节点有左叶子if(t->left!=nullptr&& t->left->left==nullptr && t->left->right==nullptr)res+=t->left->val;tra(t->left);tra(t->right);}int sumOfLeftLeaves(TreeNode* root) {tra(root);return res;}
};

计算型

对根节点分类讨论

class Solution {
public://以根节点为树的左叶子之和int sumOfLeftLeaves(TreeNode* root) {int sum=0;if(root==nullptr)return 0;//只有根节点一个if(root->left==nullptr && root->right==nullptr)return 0;//该节点的左叶子if(root->left!=nullptr&& root->left->left==nullptr && root->left->right==nullptr)sum+=root->left->val;//以root->left为树的左叶子之和int l = sumOfLeftLeaves(root->left);//以root->right为树的左叶子之和int r = sumOfLeftLeaves(root->right);return l+r+sum;}
};

112. 路径总和

操作型

顺着前序遍历的遍历走，一个结点一个结点的分析可能碰到的情况。

class Solution {
public:int sum =0;bool res=false;void tra(TreeNode* t, int target){if(t==nullptr)return;sum+=t->val;    //前序遍历 父-》当的时候把当前结点值加上if(t->left==nullptr &&t->right==nullptr){ //值已加，可以判断了if (target == sum) res = true;	           }tra(t->left,target);tra(t->right,target);sum-=t->val;                //把回溯的思想体现的淋漓尽致！！！我一开始还没有注意了。}bool hasPathSum(TreeNode* root, int targetSum) {tra(root,targetSum);return res;}
};

计算型

对根节点分类讨论。并且每个类型都有一个return
思路：当targetSum-=root->val后，如果左子树或者右子树有根路径总和==新的targetSum，那就是true；

class Solution {
public://以root为根的树路径总和是bool hasPathSum(TreeNode* root, int targetSum) {if(root == nullptr)return false;//当只有一个根节点时if(root->left==nullptr &&root->right==nullptr){targetSum-=root->val;return targetSum == 0?true:false;}//当其他情况时targetSum-=root->val;bool l =hasPathSum(root->left,targetSum);//以root->left为根路径总和bool r =hasPathSum(root->right,targetSum);return l||r;    }
};

129. 求根节点到叶节点数字之和

操作型

class Solution {
public:int sum =0;//记住二叉树的操作型算法一定记住，根节点上还有个虚拟结点。这样才能统一逻辑（和链表一样）int x =0;void sub(TreeNode* t) {if (t == nullptr)return;// 父-》当x = x * 10 + t->val;if(t->left==nullptr&&t->right==nullptr)sum+=x;sub(t->left);sub(t->right);//当-》父x/=10;}int sumNumbers(TreeNode* root) { sub(root);return sum;}
};

计算型

实力有限，这个计算型的思路太难想了。操作型简单很多。
下面是元宝给的答案。

int sumNumbers(TreeNode* root) {return dfs(root, 0);
}// 辅助DFS函数，currentSum表示从根节点到当前节点父节点的路径和
int dfs(TreeNode* node, int currentSum) {if (node == nullptr) {return 0;}// 计算到当前节点的路径和int pathSum = currentSum * 10 + node->val;// 如果是叶子节点，返回当前路径和if (node->left == nullptr && node->right == nullptr) {return pathSum;}// 如果不是叶子节点，递归计算左右子树的和return dfs(node->left, pathSum) + dfs(node->right, pathSum);
}

1448. 统计二叉树中好节点的数目

操作型

错误答案

class Solution {
public:int tmp=INT_MIN;int count = 0; void tra(TreeNode* t){if(t==nullptr)return ;if(t->val >= tmp){count++;tmp=t->val;  }          tra(t->left);tra(t->right);//回溯时（子=》当）如何再将tmp恢复了。我发现当递归返回到父节点时，tmp的值已经被子节点修改了，导致后续节点判断错误。所以不能用全局变量做tmp；}int goodNodes(TreeNode* root) {     tra(root);   return count;  }
};

依旧错误

使用引用传递的正确答案

class Solution {
public:int count = 0; void tra(TreeNode* t,int& tmp){if(t==nullptr)return;int original_tmp = tmp;  // 保存进入当前节点前的tmp值   // 更新了路径上的最大值if(t->val >= tmp){count++;tmp=t->val;  }  tra(t->left,tmp);tra(t->right,tmp);//回溯时（子=》当）如何再将tmp恢复？tmp = original_tmp;  // 回溯：恢复tmp为进入当前节点前的值}int goodNodes(TreeNode* root) {     int tmp= INT_MIN;tra(root,tmp);   return count;  }
};

使用值传递，就不需要回溯tmp值了。可以这样理解， tra(t->left,tmp)有一个栈，保存了tmp的信息，所以就不用回溯了。！！！

class Solution {
public:int count = 0; void tra(TreeNode* t,int tmp){if(t==nullptr)return;// 更新了路径上的最大值if(t->val >= tmp){count++;tmp=t->val;  }  tra(t->left,tmp);tra(t->right,tmp);}int goodNodes(TreeNode* root) {     int tmp= INT_MIN;tra(root,tmp);   return count;  }
};

计算型

计算型越来越难想了。
分类讨论不再是p是否有结点，而是分类讨论p是否是好节点

class Solution {
public:int tra(TreeNode* t,int tmp){if(t==nullptr)return 0;if(t->val>=tmp){tmp=t->val;return tra(t->left,tmp)+tra(t->right,tmp)+1;}return tra(t->left,tmp)+tra(t->right,tmp);}int goodNodes(TreeNode* root) {int tmp =INT_MIN;return tra(root,tmp);}
};