数据结构**优先级队列**超详细入门到进阶宝典

“成功就是一把梯子，双手插在口袋的人是爬不上去的”

1. 前言

本文主要围绕优先级队列展开，优先级队列也属于二叉树部分的收尾内容！请大家跟进小编的步伐！！ 🌹🌹🌹

---

2. 正文

1. 优先级队列

1.1 什么是优先级队列？

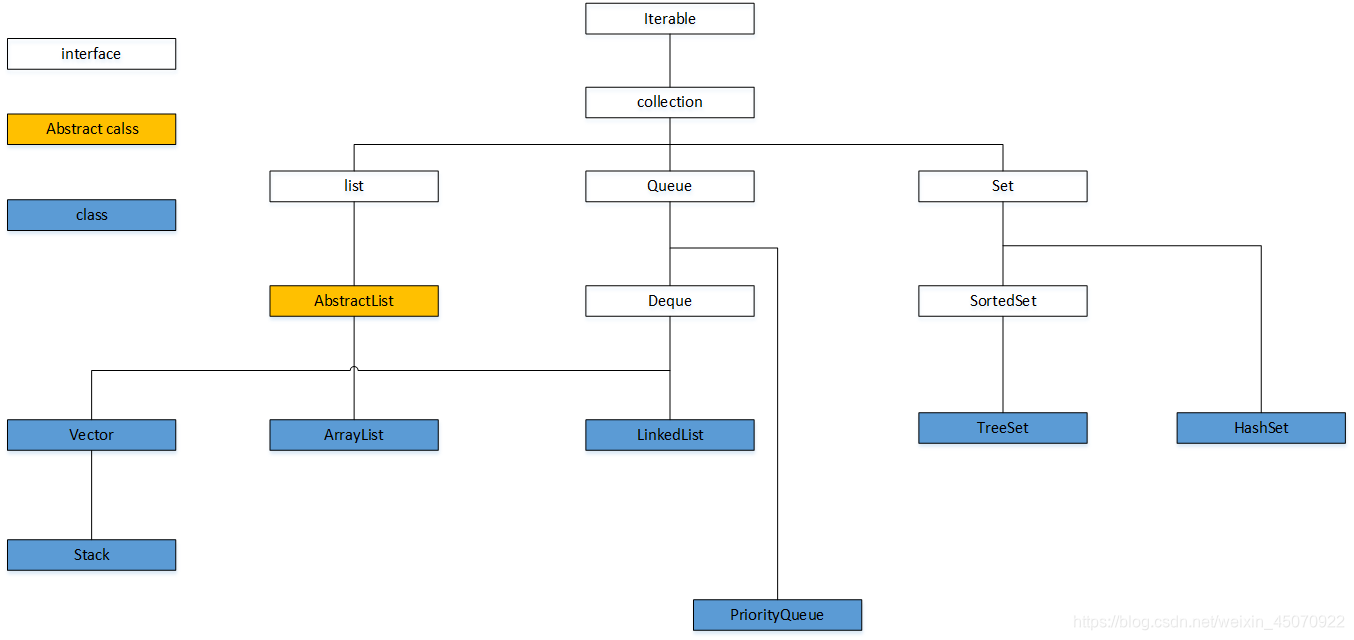
还是看我们的老朋友这张图片，我们的优先级队列就是正下方的PriorltyQueue，我们在前面的学习中掌握了队列Queue这个数据结构，而PriorltyQueue继承与队列，也被叫做优先级队列！
在我们的生活中处处充满了优先级队列的知识，比如你正在打游戏，可能突然显示有人来电，此时屏幕就会切换成来电显示，这就是优先级高的元素先出队列了。

---

1.2 优先级队列的底层

优先级队列的底层采用了堆这个数据结构，堆是顺序存储的结构，所以我们可以理解为优先级队列是二叉树的顺序存储所实现的。

---

2. 堆

2.1 什么是堆？

堆就是把它的所有元素按完全二叉树的顺序存储方式存储，存储在一个一维数组中

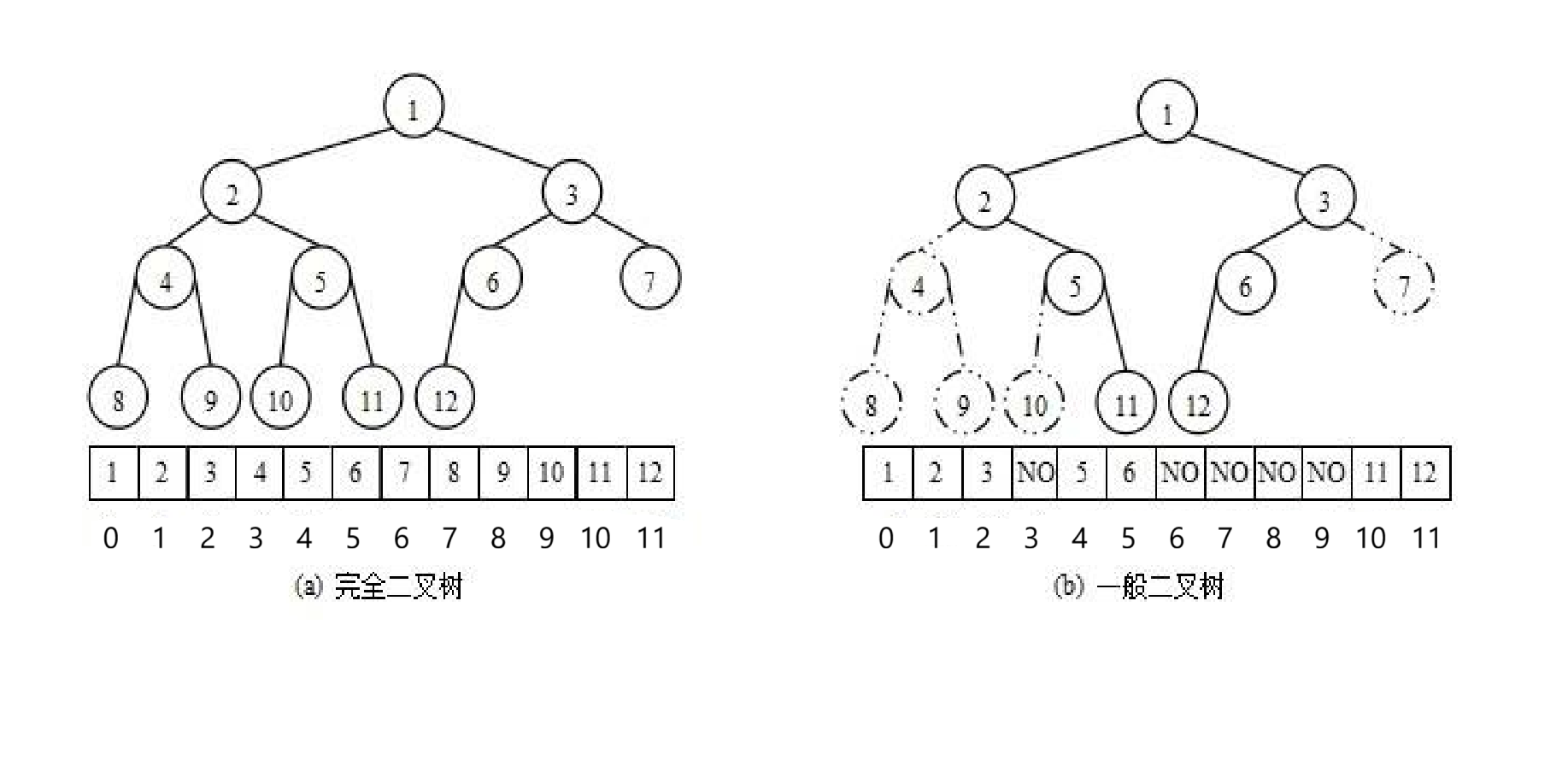我们可以看到如果存储的是非完全二叉树，数组中会有空的元素而浪费空间，空间利用率低，所以我们的堆最好是一棵完全二叉树

---

2.2 堆的性质

我们的堆分为以下两种结构： 大根堆和小根堆

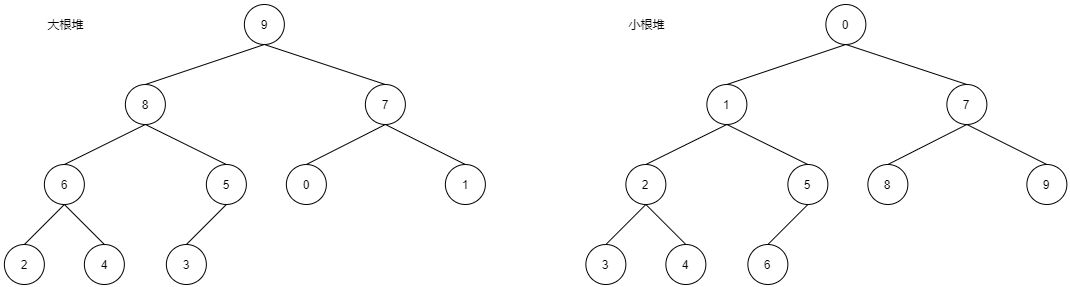
大根堆要求每棵树的根结点必须大于左右子树
小根堆要求每棵树的根结点必须小于左右子树
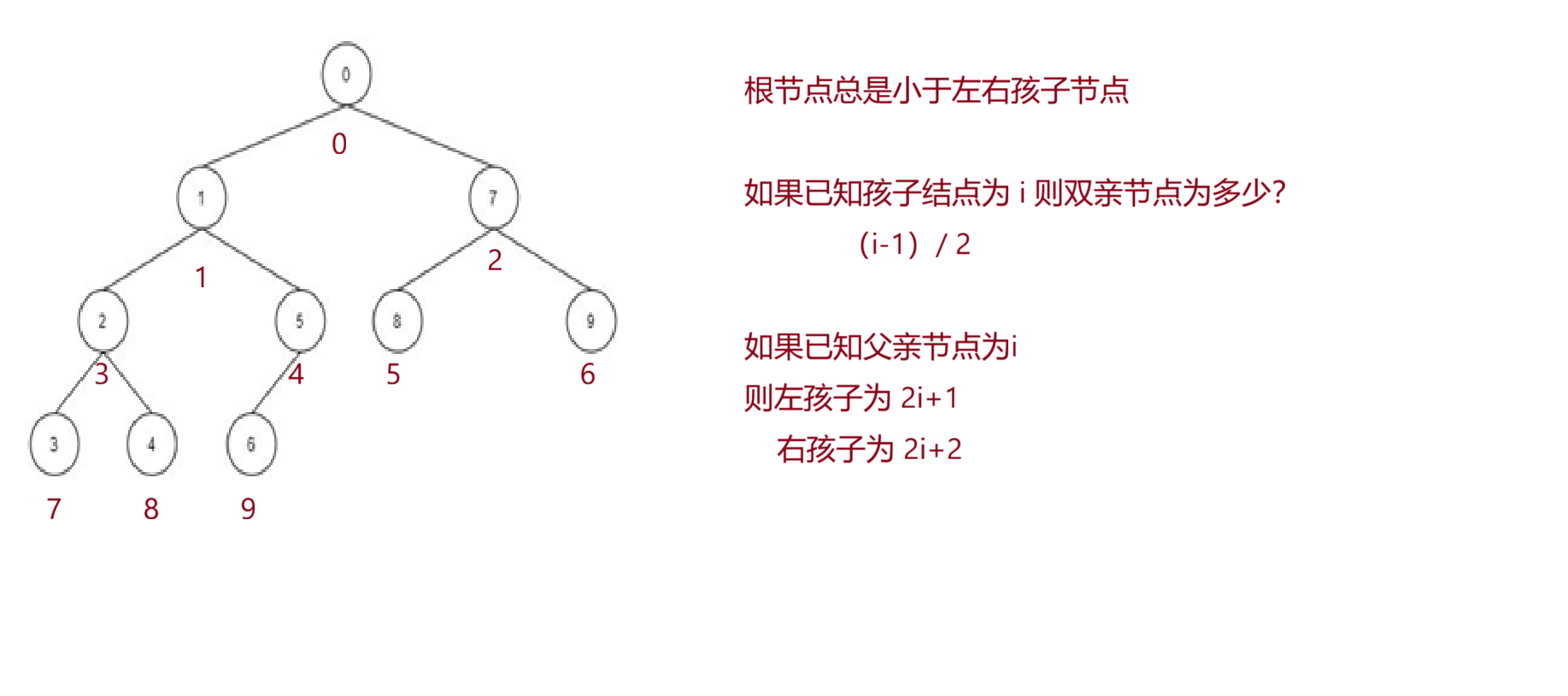以上就是堆的性质

---

2.3 自己实现 堆 数据结构

1. 首先我们先搭框架

public class TextHeap {public int[]elem;public int useSize;public TextHeap() {this.elem = new int[10];}public void initElem(int[]array){for (int i = 0; i < array.length; i++) {this.elem[i]=array[i];}}
}

这里的构造方法给我们的elem初始分配空间，initElem方法是为了给elem初始化。

---

2. creatHeap（）方法，创建一个大根堆，这里我们采用向下调整建堆
   

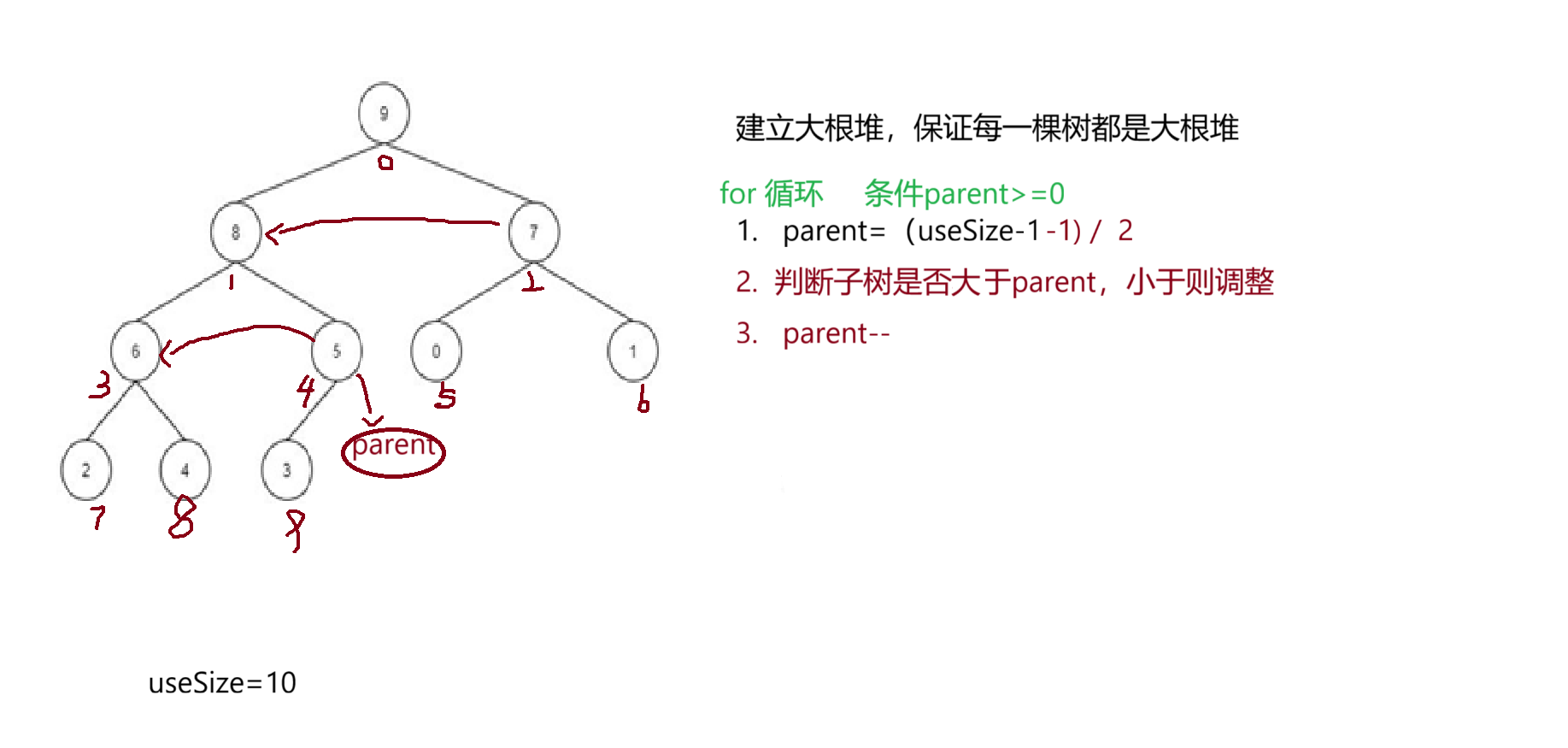
png)我们先完成这部分的框架

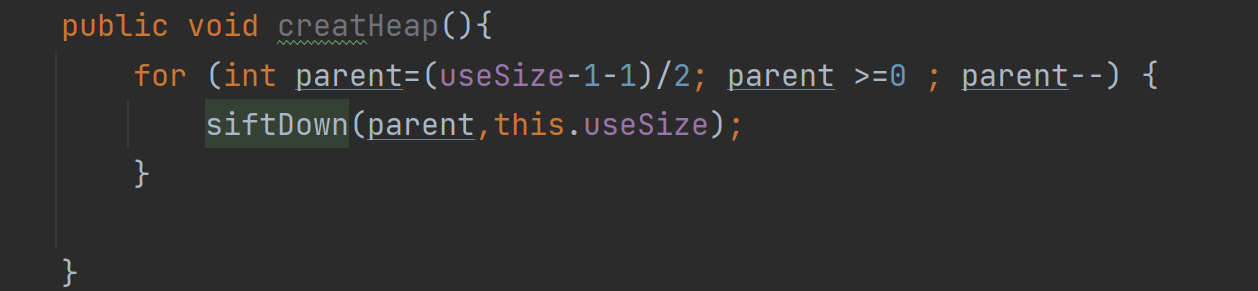
我们这里只需要完成siftdown方法，里面的参数是从parent当前位置调整，调整到useSize位置

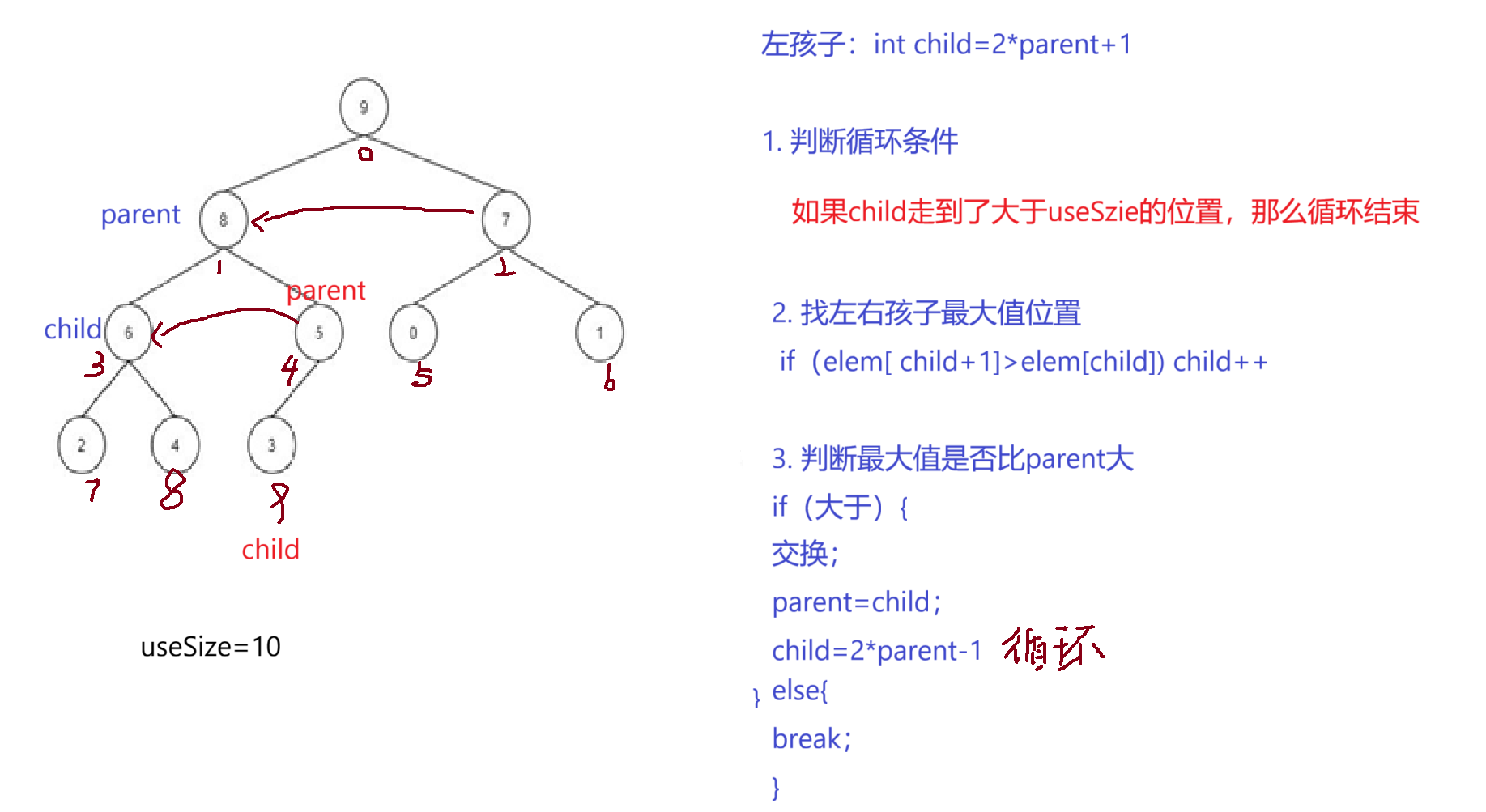
这里有小伙伴有疑问，如果elem[parent]大于elem[child]直接break可以吗？因为我们这里是大根堆，如果parent大于child当前位置的值，那么parent肯定大于child以下所有位置的值

public void siftDown(int parent,int useSize){int child=2*parent+1;while(child<useSize){if(child+1<useSize && elem[child+1]>elem[child]){child++;}if(elem[parent]<elem[child]){int tmp=elem[parent];elem[parent]=elem[child];elem[child]=tmp;parent=child;child=2*parent+1;}else{break;}}}

这里我们在child+1中加入一个条件就是如果child+1越界了，那么我们直接去child即可。
这里我们关注一下向下调整的时间复杂度为多少呢？
答案是O（N），很多人可能认为时间复杂度为NlogN，这里我们通过公式推导
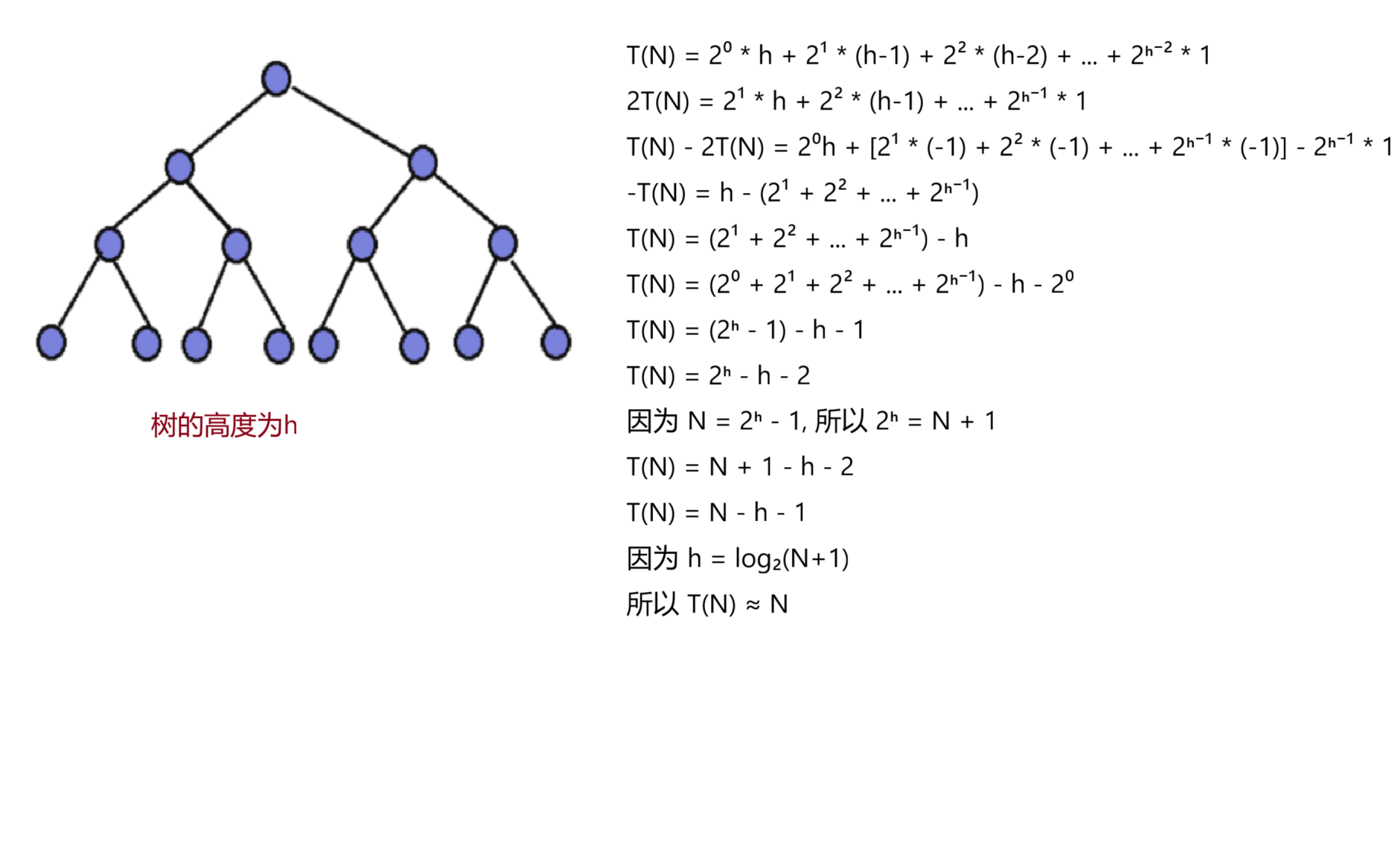这里我们得出时间复杂度为O（N）

---

3. pushVal(int val)方法，我们要在堆中加入新的元素使用这个方法。
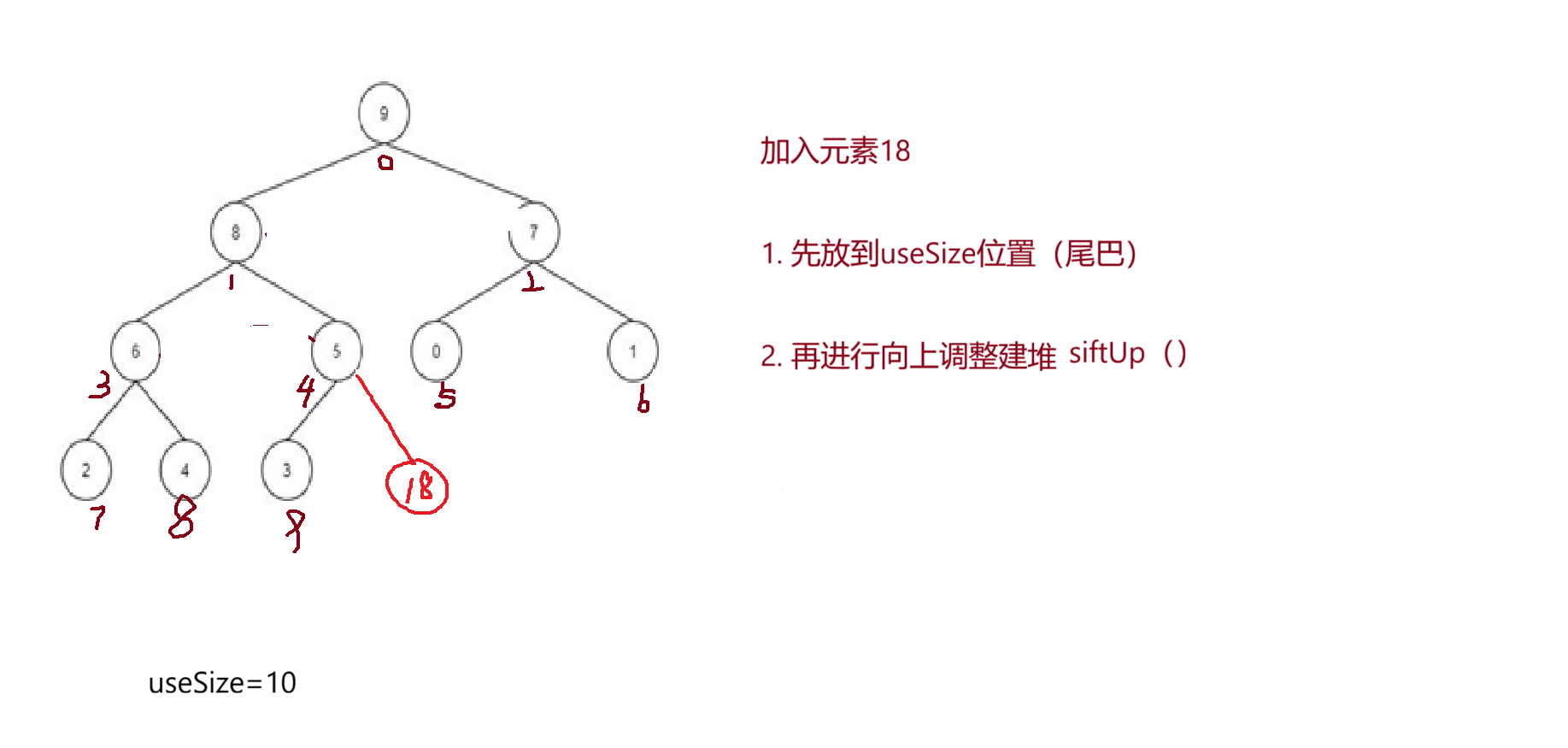   这里我们采用了向上调整建堆，我们先搭建框架

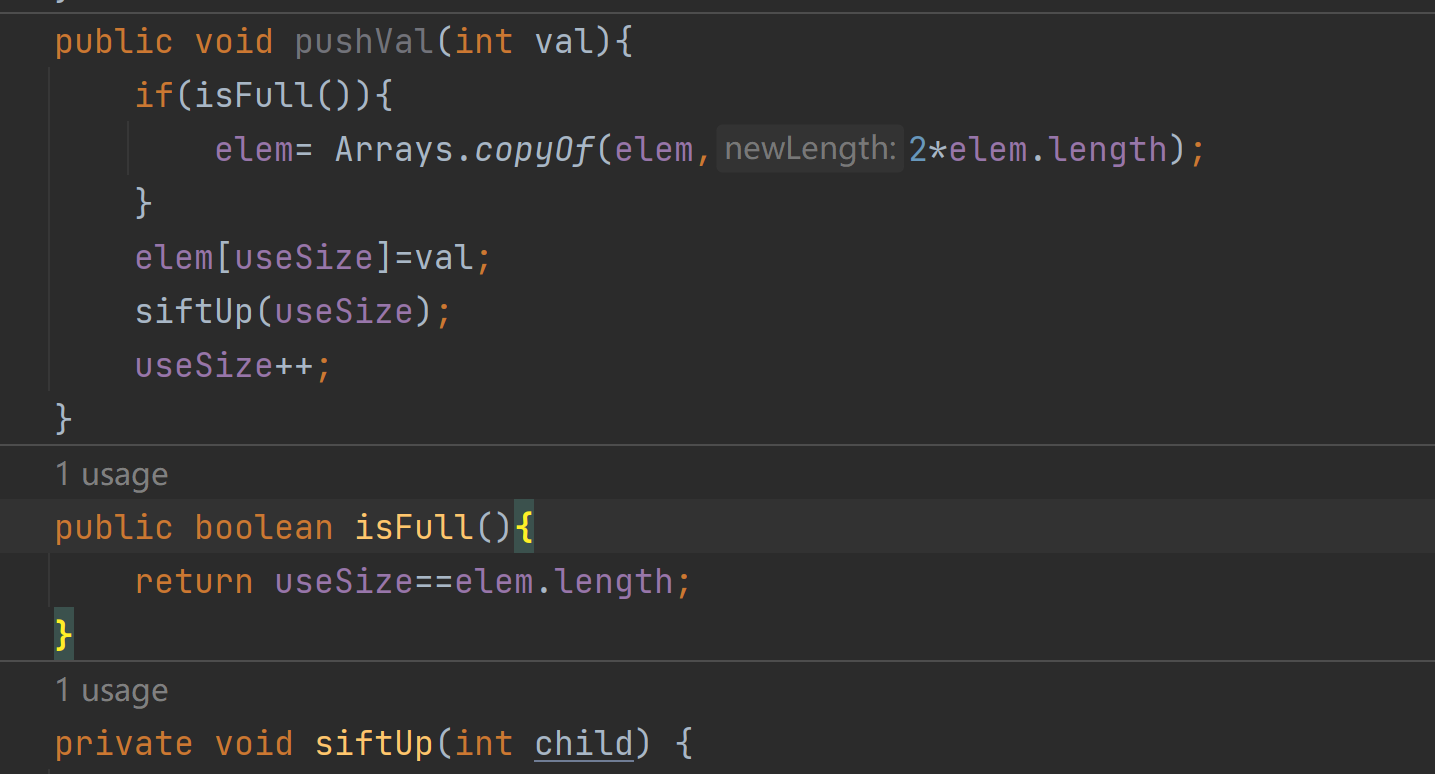这里siftUp传入的参数是当前child的位置，下面完善siftUp方法

private void siftUp(int child) {int parent=(child-1)/2;while(parent>=0){if (elem[child]>elem[parent]){int tmp=elem[parent];elem[parent]=elem[child];elem[child]=tmp;child=parent;parent=(child-1)/2;}else {break;}}}

先确定parent的位置，循环条件为parent>0，如果当前child位置的元素大于parent位置我们直接交换即可，这里不用判断child-1，因为原本的堆就是一个大根堆，child-1位置的值一定小于parent位置的值！
我们这里关注一下时间复杂度为O（NlogN），这里就不再进行推导，与向下调整建堆的思路一样，但是效率没有向下调整高

---

4. poll（）方法，用来删除元素
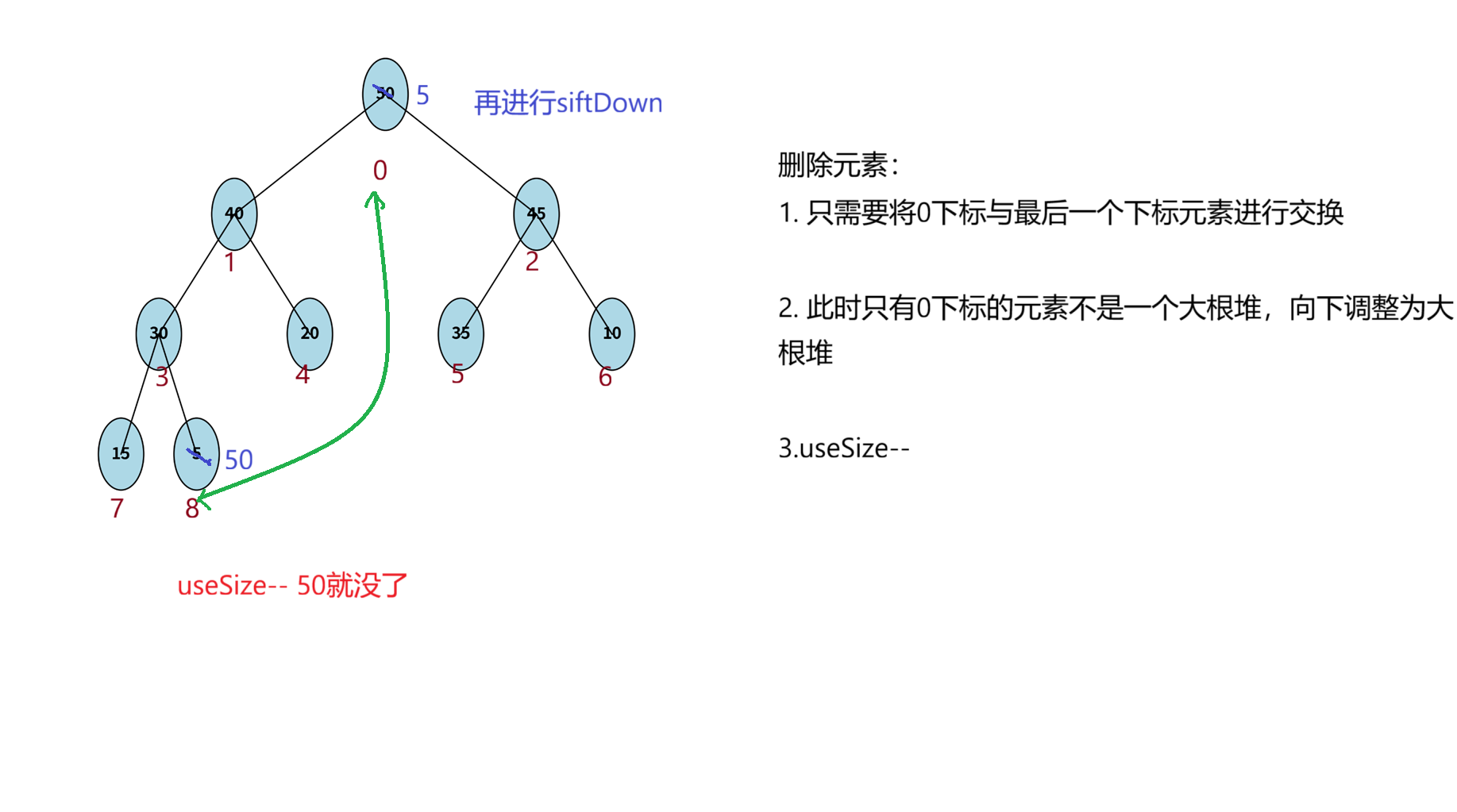   我们来完成这部分的代码
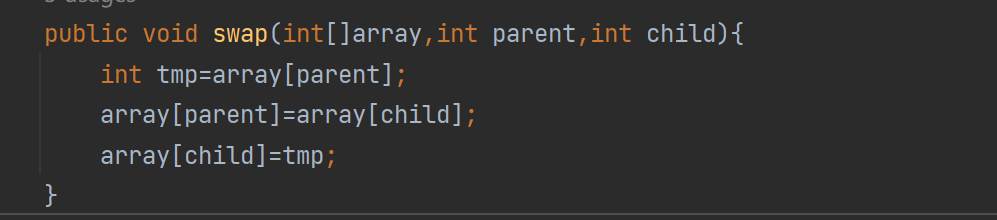   首先我们把swap交换写成一个方法，这样调用就方便了

  public int poll(){int val=elem[0];swap(elem,0,useSize-1);siftDown(0,useSize-1);useSize--;return val;}

此时siftDown传入的是useSize-1，因为50这个元素要被删去就不需要注意了。

---

剩余还有很多方法例如peek() ,isEmpty()… 小编在这就不一一实现了，原理都与我们之前实现的数据结构相同，代码详解在这🌹

---

2.4 堆练习题

1. 下列关键字序列为堆的是:()
   A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60
   D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 F: 50,100,70,65,60,32

由画图我们可以得出答案选择A

---

2. 已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是()
   A: 1 B: 2 C: 3 D: 4

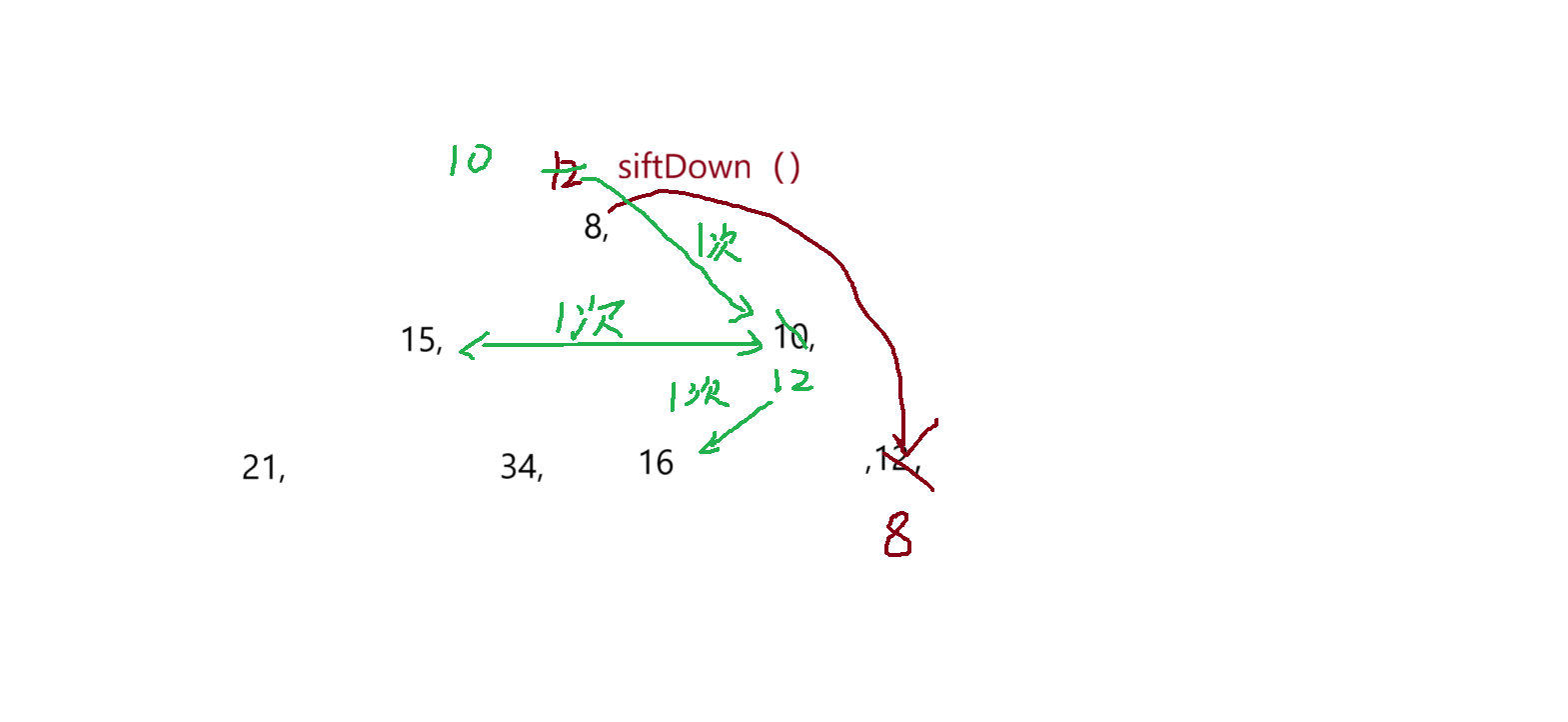
所以选C

---

3. 最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是()
   A: [3，2，5，7，4，6，8] B: [2，3，5，7，4，6，8]
   C: [2，3，4，5，7，8，6] D: [2，3，4，5，6，7，8]

与2类似也是画图实现，选C

---

2.5 堆的应用

我们这里主要用堆这个数据结构来实现排序

首先我们要判断应该是建立大根堆还是小根堆
答案是大根堆，如果建立的是小根堆只能判断堆顶元素为最小元素，剩下的元素均为乱序，而大根堆则不一样

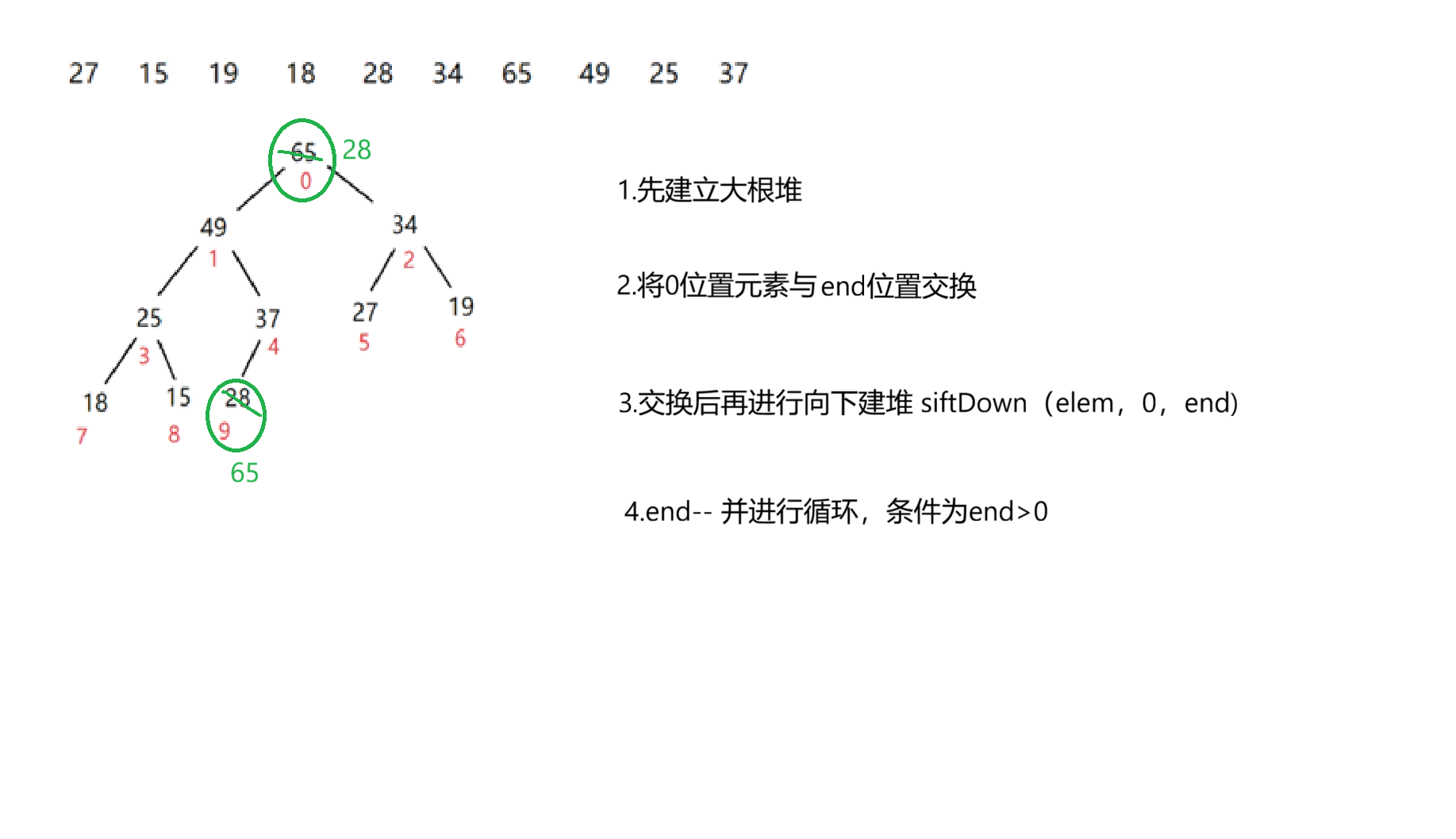
   public void heapSort(){int end=useSize-1;while (end>0){swap(elem,0,end);siftDown(0,end);end--;}}

如上就是堆排序，堆排序的时间复杂度为O（NlogN），在后面的学习中我们会专门学习排序这一章节，其中就包括堆排序！

---

3. PriorltyQueue

3.1 PriorltyQueue特性

PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线
程不安全的，PriorityBlockingQueue是线程安全的，我们这里主要介绍PriorityQueue

---

3.2 PriorltyQueue在Java的实现

1. 首先PriorltyQueue是一个类，底层是堆这个数据结构，实现Queue接口，所以关于PriorltyQueue的声明有如下两种

        PriorityQueue<Integer> priorityQueue=new PriorityQueue<>();Queue<Integer> priorltyQueue2=new PriorltyQueue<>();

2. 下面我们看一下 PriorityQueue的方法
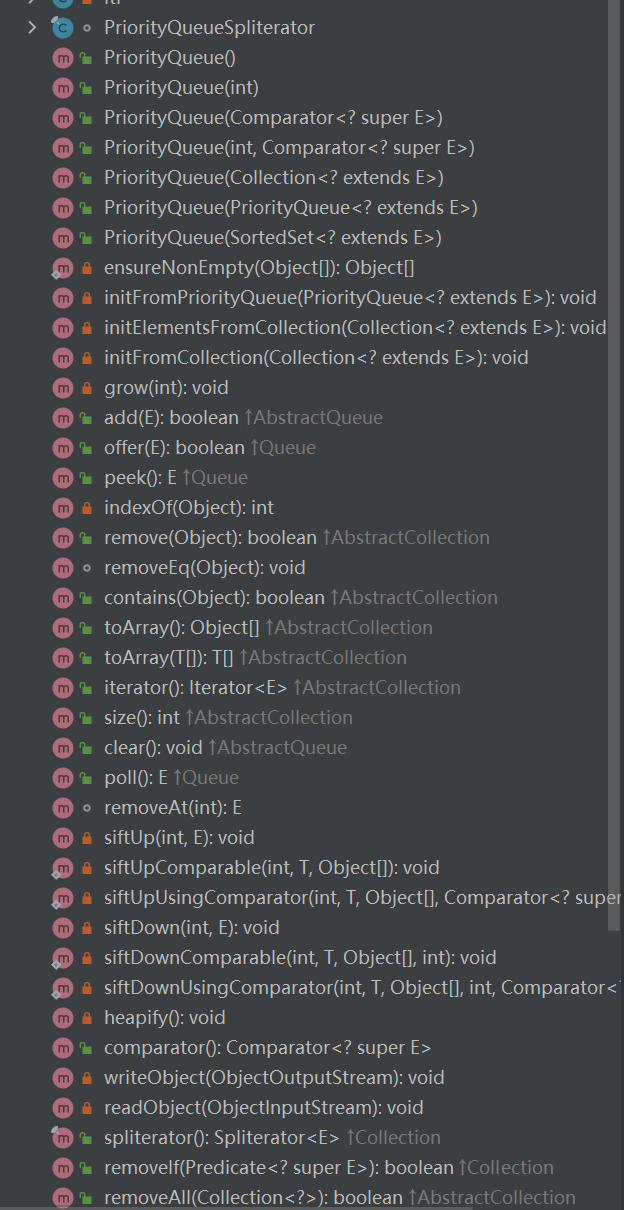   这与我们的队列数据结构中的方法很相似。
3. PriorltyQueue的底层是一个大根堆还是一个小根堆？
   
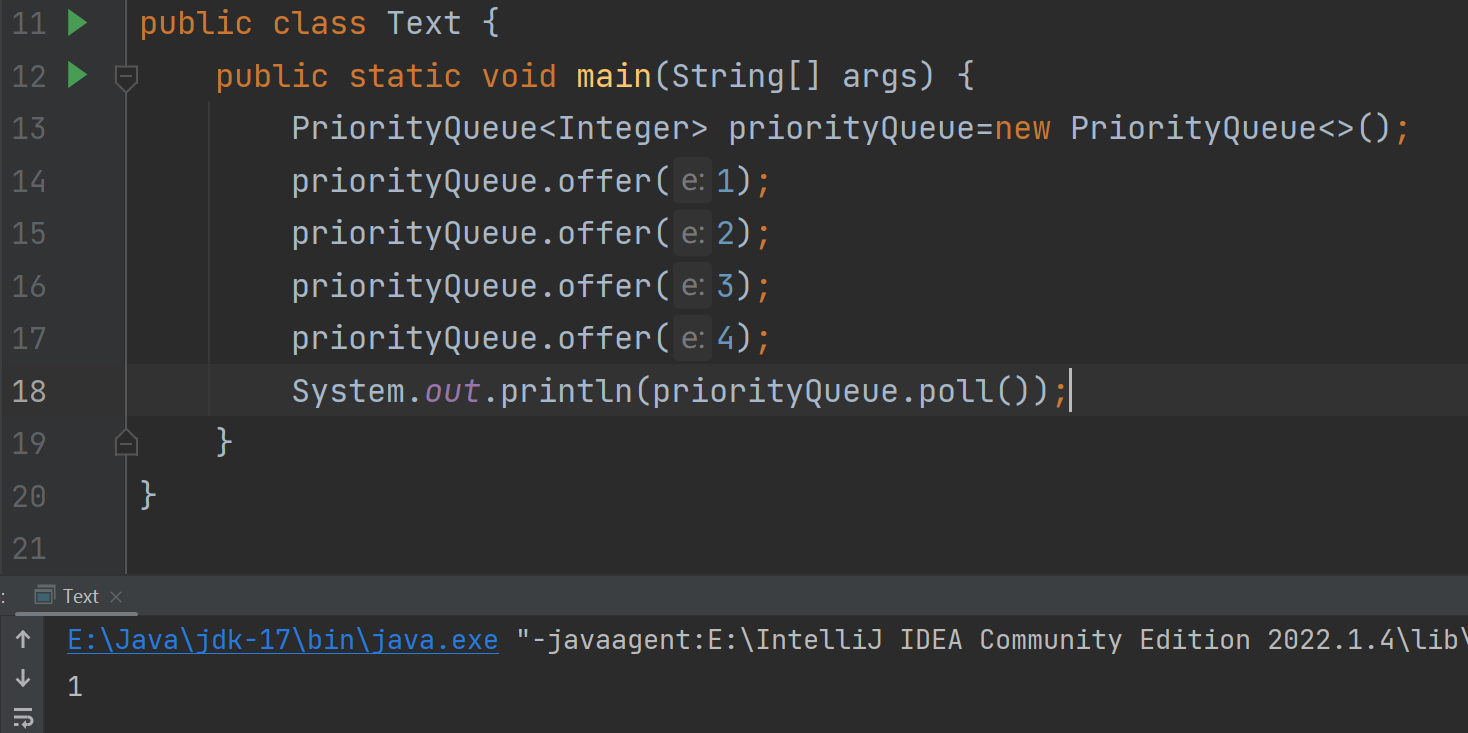
   根据这个结果显示，PriorltyQueue默认是小根堆、

---

4. PriorityQueue的构造方法
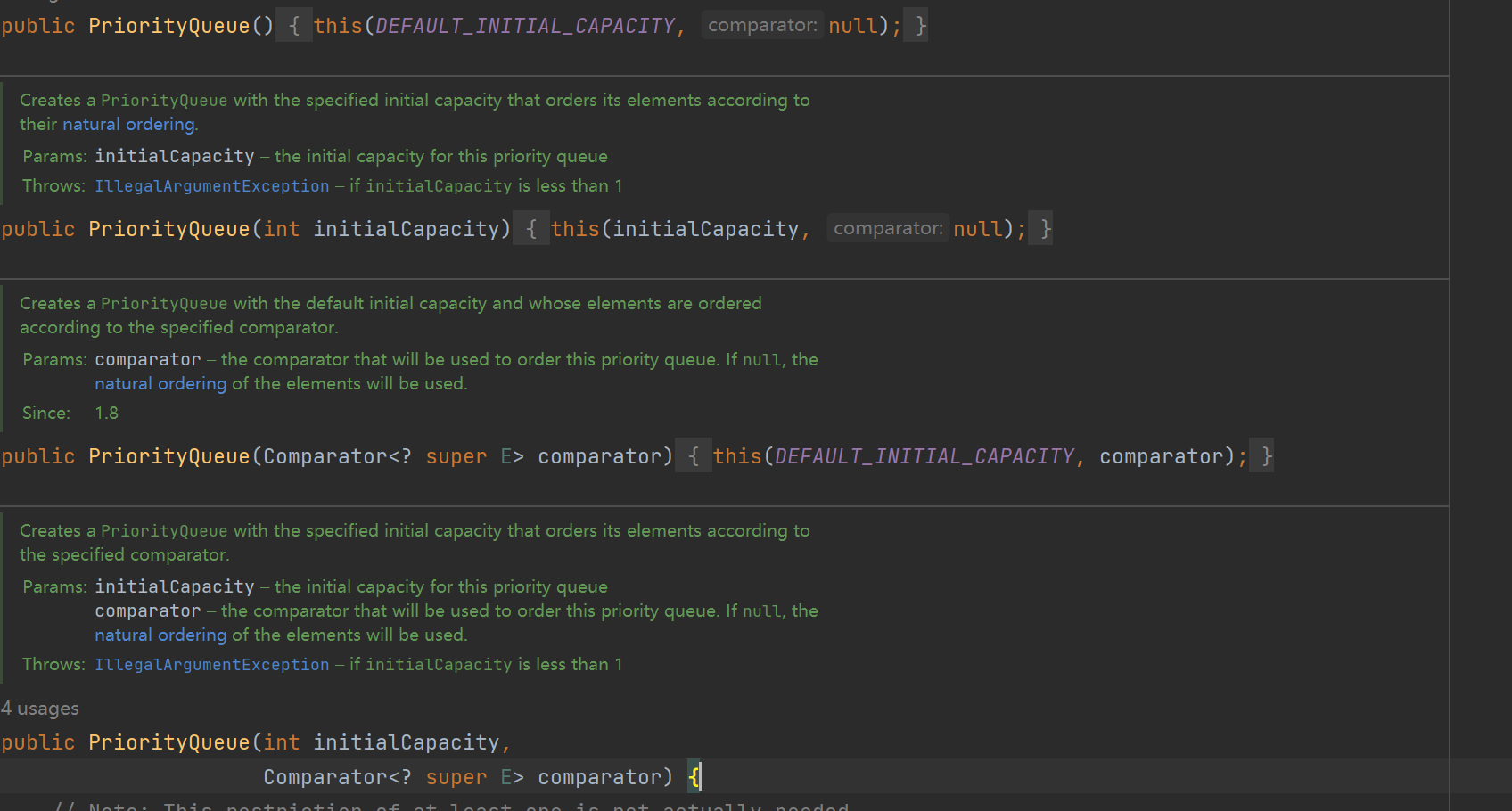   我们只看前三个构造方法即可，首先来看第一个

   第一个构造方法是不带参数的构造方法其中DEFAULT_INITIAL_CAPACITY是初始容量
   
   我们可以看到初始容量为11

   第二个构造方法是传一个参数的构造方法，创建一个初始容量为initialCapacity的优先级队列

   第三个构造方法就是传入一个集合。

   这三个构造方法都调用了带两个参数的构造方法
   
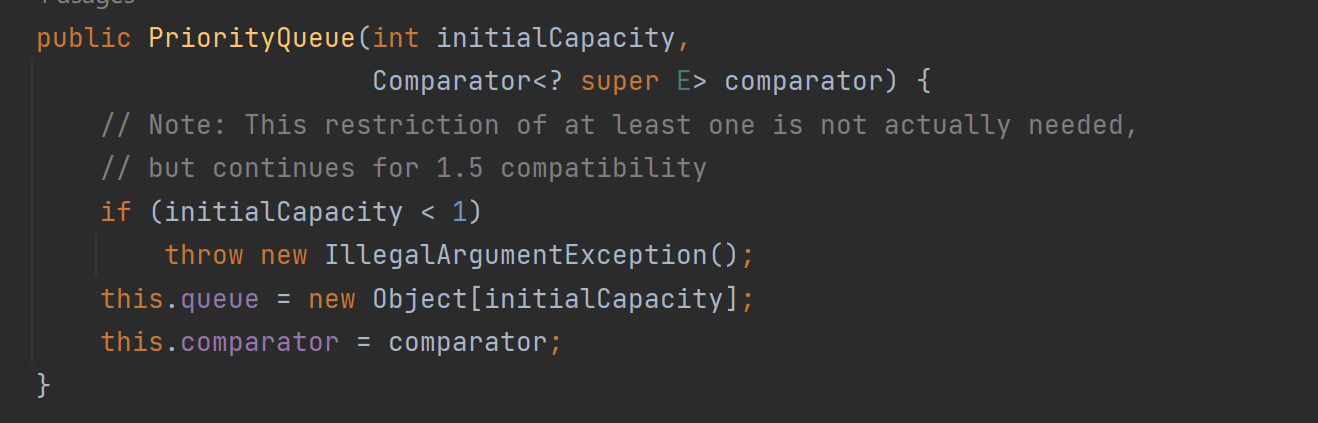
   都调用了如上方法
   

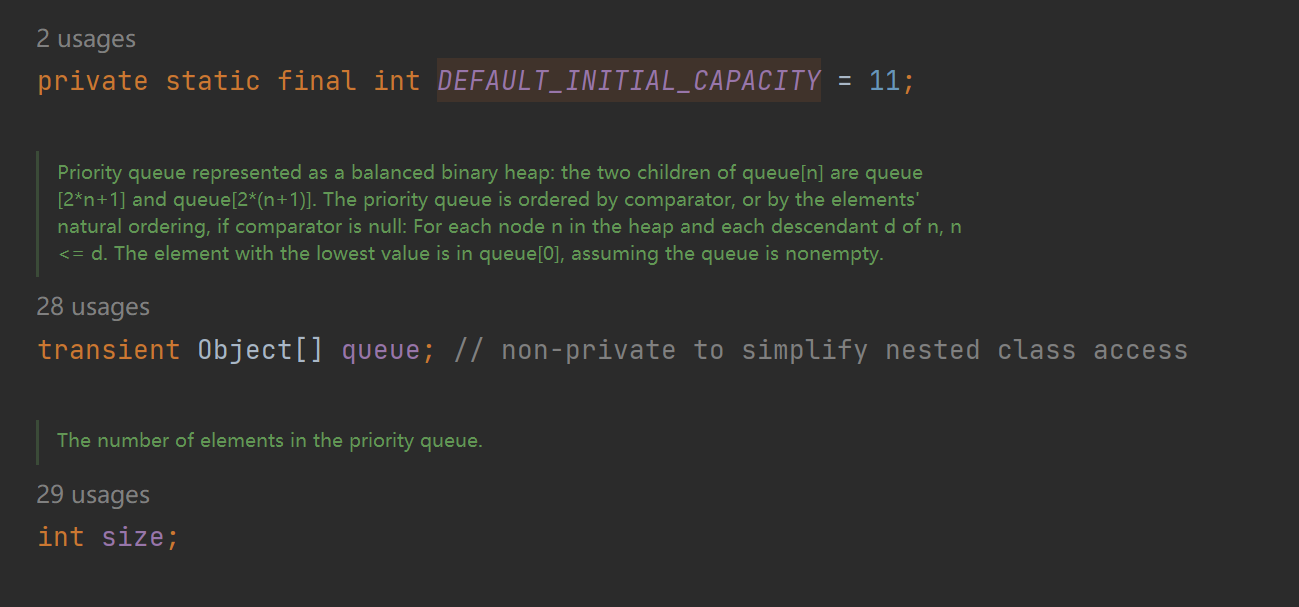
   这里的queue就是我们定义的elem！

---

3.3 PriorltyQueue使用的注意事项

1. PriorityQueue中添加（offer（））的元素必须要能够比较大小或者是实现Comparable或Comparator接口的自定义类，否则不能插入无法比较大小的对象，否则会抛出ClassCastException异常
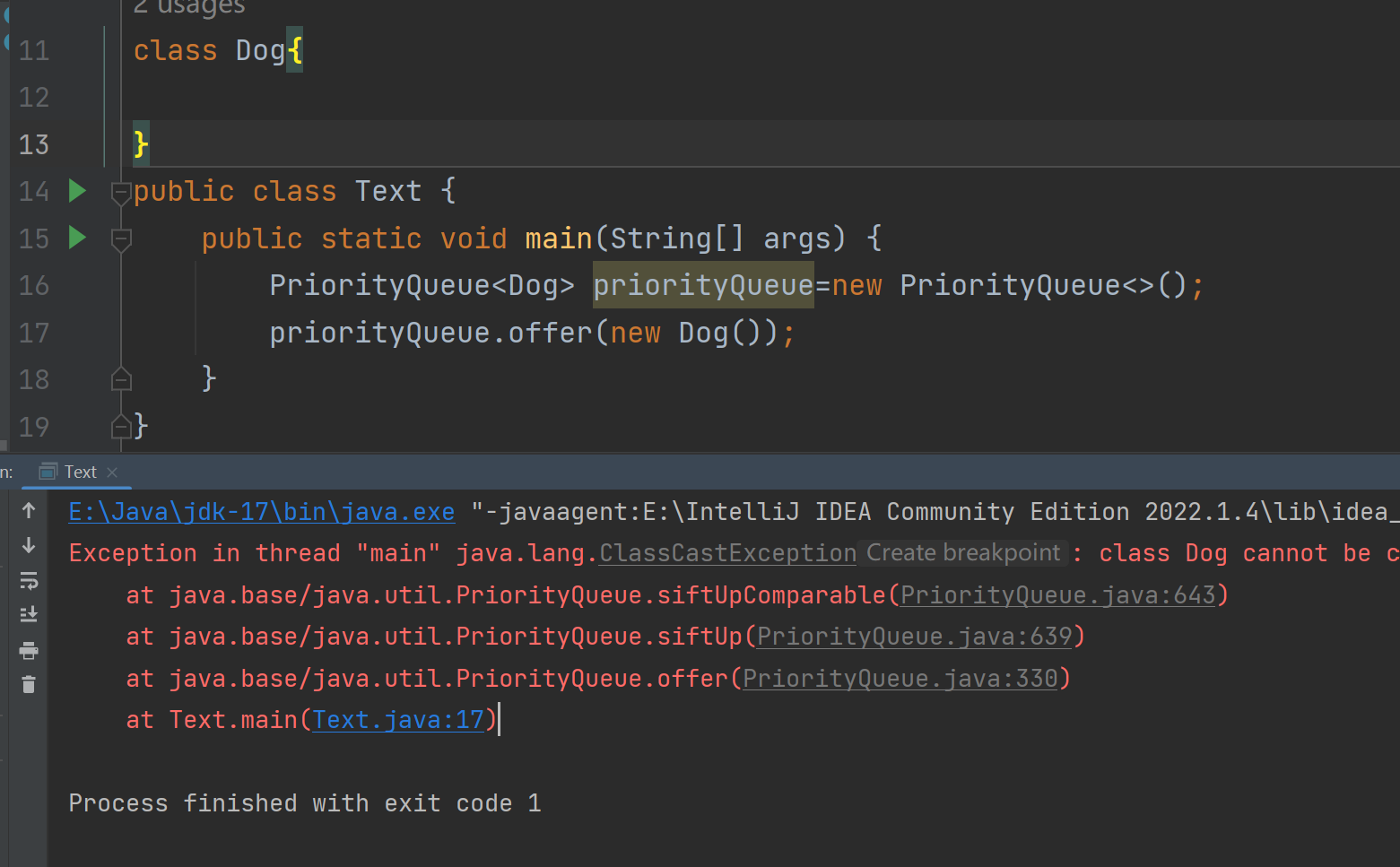   我们来看看出错的643行
   这里说明在offer任何一个元素之前都要强转成Comparable接口。

---

2. PriorityQueue不能添加null对象，否则会抛出NullPointerException

---

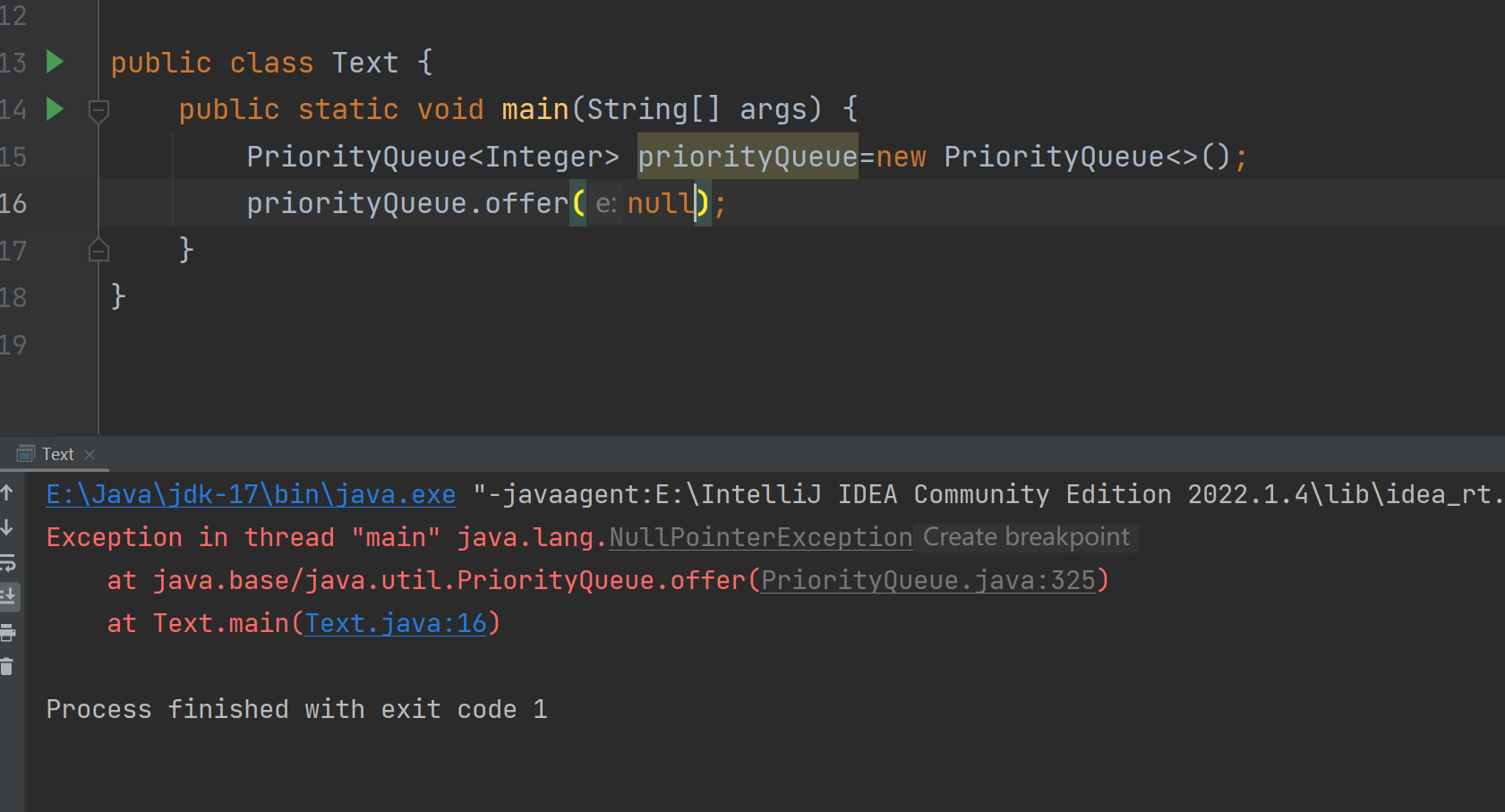
3. PriorityQueue没有容量限制，可以插入添加任意多个元素，其内部可以自动扩容

   我们来看一下offer的源码
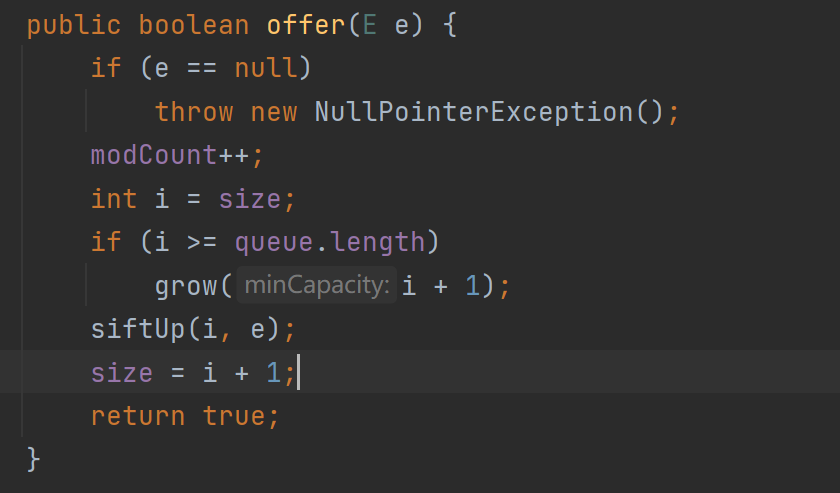   我们可以看到offer里面有grow扩容方法
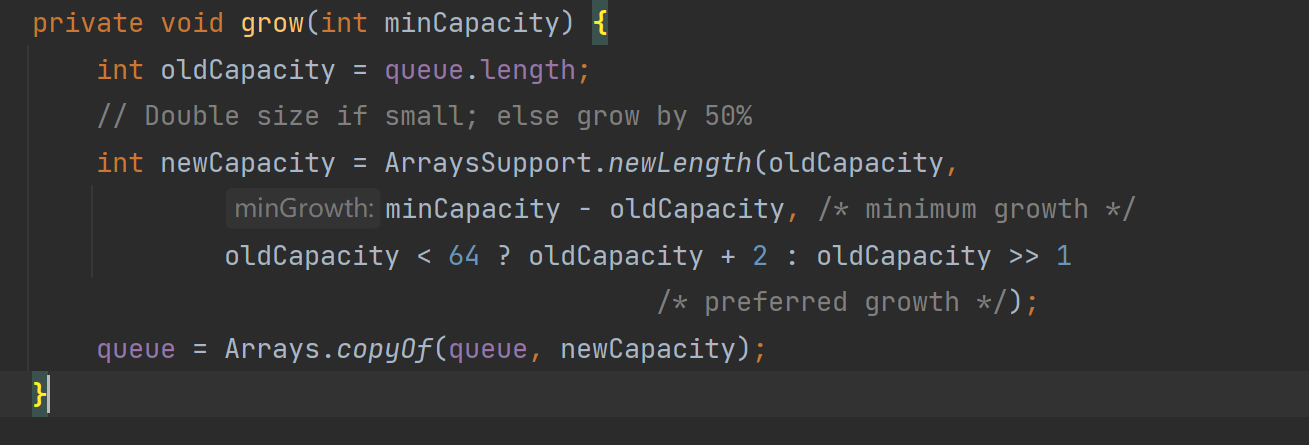   这里的意思就是将queue数组很小进行2倍扩容，很大就1.5倍扩容

---

4. PriorityQueue插入和删除元素的时间复杂度为O（logN）

---

3.4 PriorityQueue底层变为大根堆

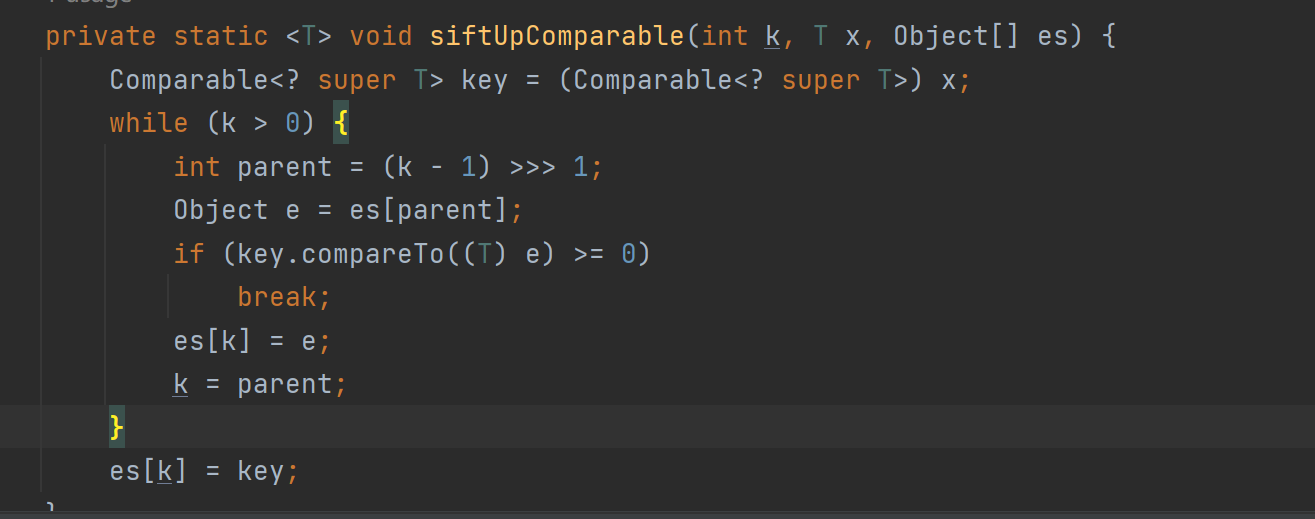
这张图是PriorityQueue向上调整的源码，我们可以看到其中key是新放入的元素，
key.compareTo((T)e) ，return key.cal-e.val ，如果key小的话就要换，才建立成小根堆，如果这里我想建立大根堆只需调换一下位置即可

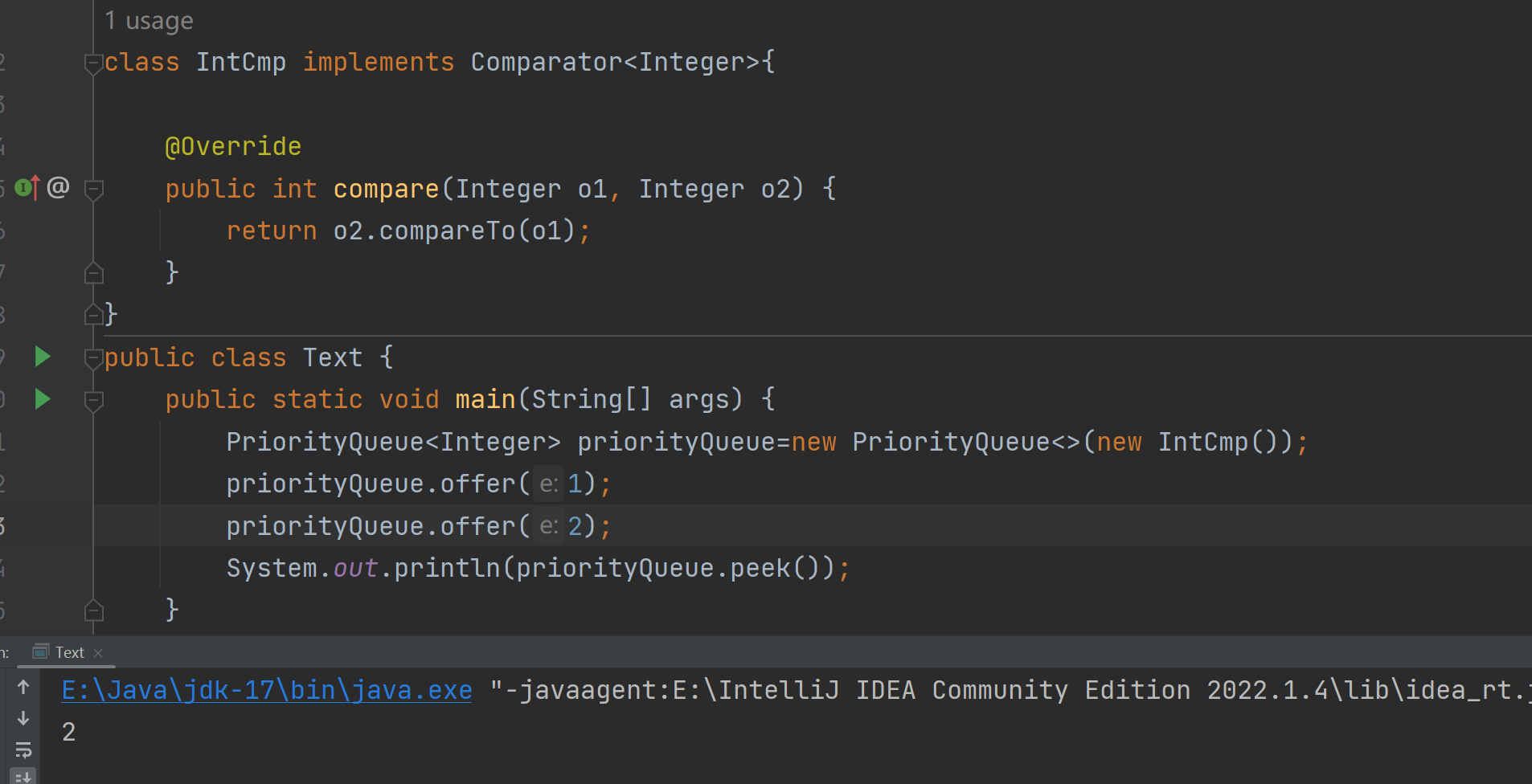这样我们就成功建立起一个大根堆了！

---

4. TopKey问题

TopKey问题，找出数组中最小的k个数。以任意顺序返回这k个数均可。
这里我们的思路有三种

1. 整体排序
2. 一共有N个数，建立一个大小为N的小根堆，返回头部的元素放入数组，再进行小根堆排序直到排到第K个元素
3. 把前K个元素建立为大根堆，遍历剩下的N-K个元素，与堆顶元素比较，如果比堆顶元素小，则替换堆顶元素，再进行大根堆排序，这样我们的堆顶元素就是前K个第K小的元素

我们的第一种思路小编就不完成代码了，因为很简单，首先我们先完成第三种思路的代码

class Solution {public int[] smallestK(int[] arr, int k) {int []elem=new int[k];if(arr==null||k==0){return elem;}     PriorityQueue<Integer> priorityQueue=new PriorityQueue<>(new IntCmp());for(int i=0;i<k;i++){priorityQueue.offer(arr[i]);}for(int i=k;i<arr.length;i++){int val=priorityQueue.peek();if(val>arr[i]){priorityQueue.poll();priorityQueue.offer(arr[i]);}}for(int i=0;i<k;i++){elem[i]=priorityQueue.poll();}return elem;}
}
class IntCmp implements Comparator<Integer>{public int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}

这个代码的完成紧贴思路，如果遇到比堆顶元素小的就出堆，放入新的元素，再排序

下面是第二种思路完成的代码

 public int[] smallestK1(int[] arr, int k) {PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {priorityQueue.offer(arr[i]);}int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}

这个思路完成虽然简单，但是算法不如第三种思路，所以我们这里主要要理解第三种思路的完成。

---

以上就是优先级队列的所有内容，我们可以看到优先级队列中包括对象的比较的知识，如果这部分知识不牢固 看这边！！！，这里详细介绍了对象的比较的两种接口！

---

3. 结语

以上就是本文主要的内容，我们已经攻克了二叉树所有的基础学习，下面小编会讲解七大排序，使我们的编码能力更上一层楼！有不明白的地方可以留言小编会回复，希望读者们多提建议，小编会改正，共同进步！谢谢大家。🌹🌹🌹