[优选算法专题六.模拟 ——NO.40~41 外观数列、数青蛙]

题目链接

38. 外观数列

题目描述

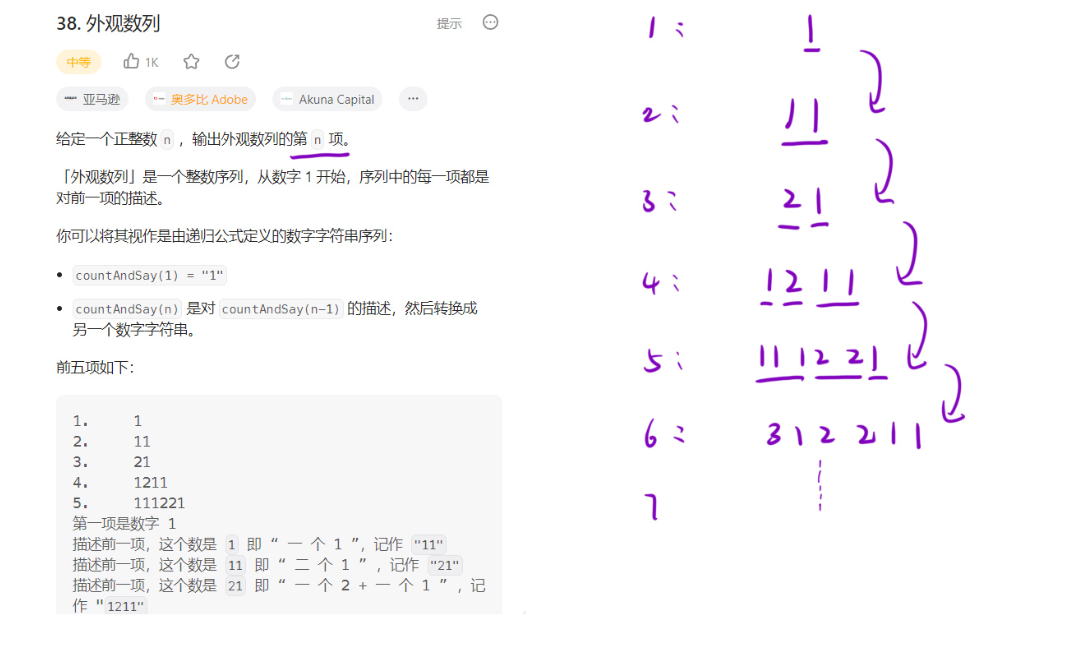
题目解析：

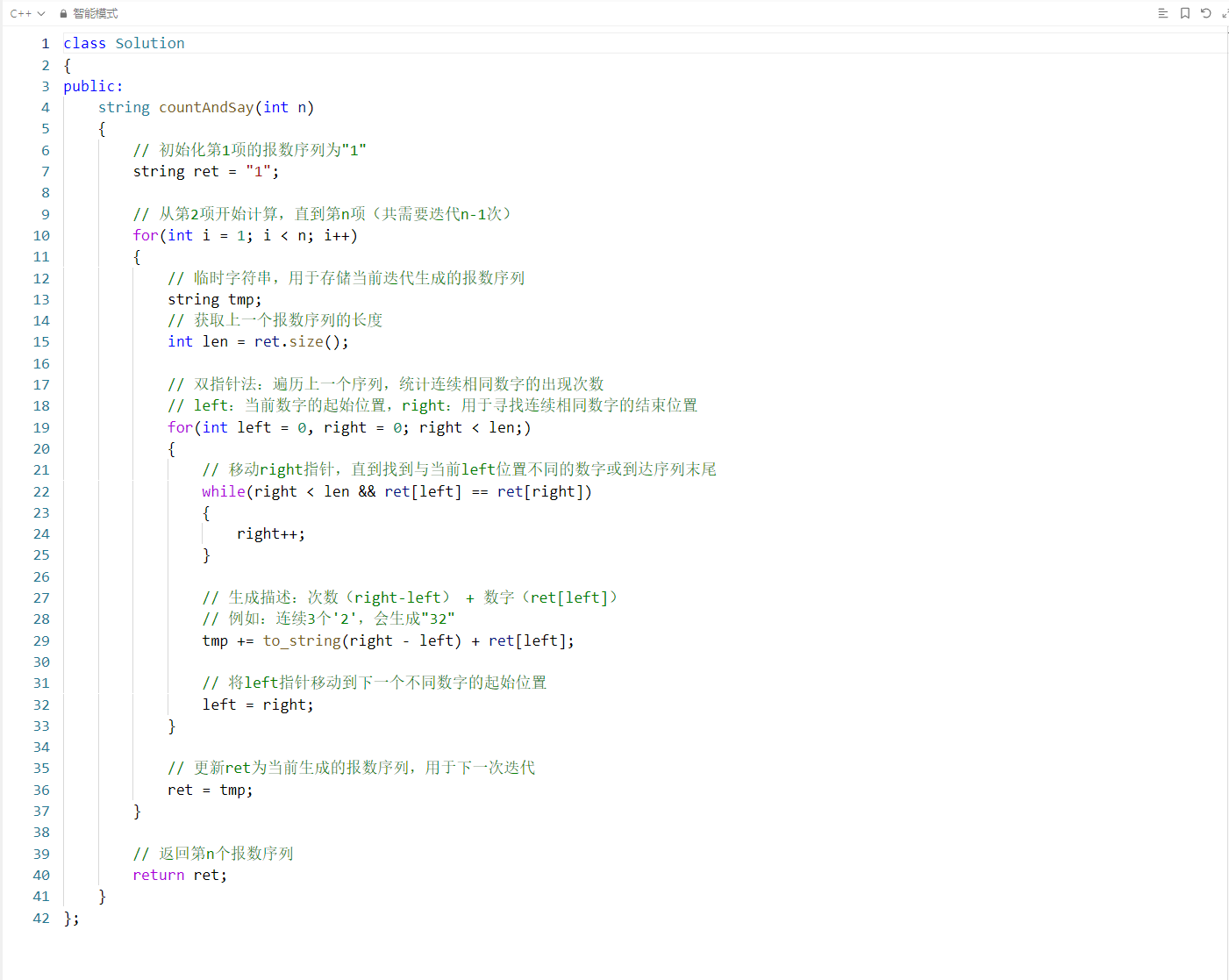
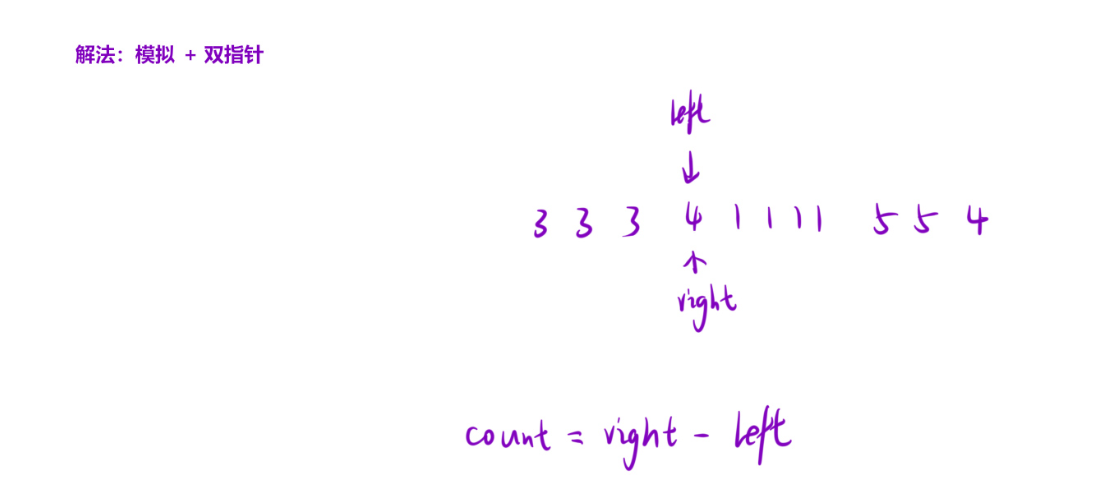
核心逻辑说明：

1. 初始条件：第 1 个报数序列固定为 "1"
2. 迭代生成：从第 2 项到第 n 项，每次都以上一项为基础生成新序列
3. 双指针技巧：
   • left 标记当前数字的起始位置
   • right 向前移动找到连续相同数字的结束位置
   • 两者的差值（right-left）就是当前数字的出现次数
4. 字符串拼接：将 "次数 + 数字" 的组合拼接到临时字符串，形成新的报数序列

时间复杂度：O(2^n)（指数级，随 n 增长快速增大）

空间复杂度：O(2^n)（指数级，主要用于存储中间序列）

---

题目链接

1419. 数青蛙

题目描述

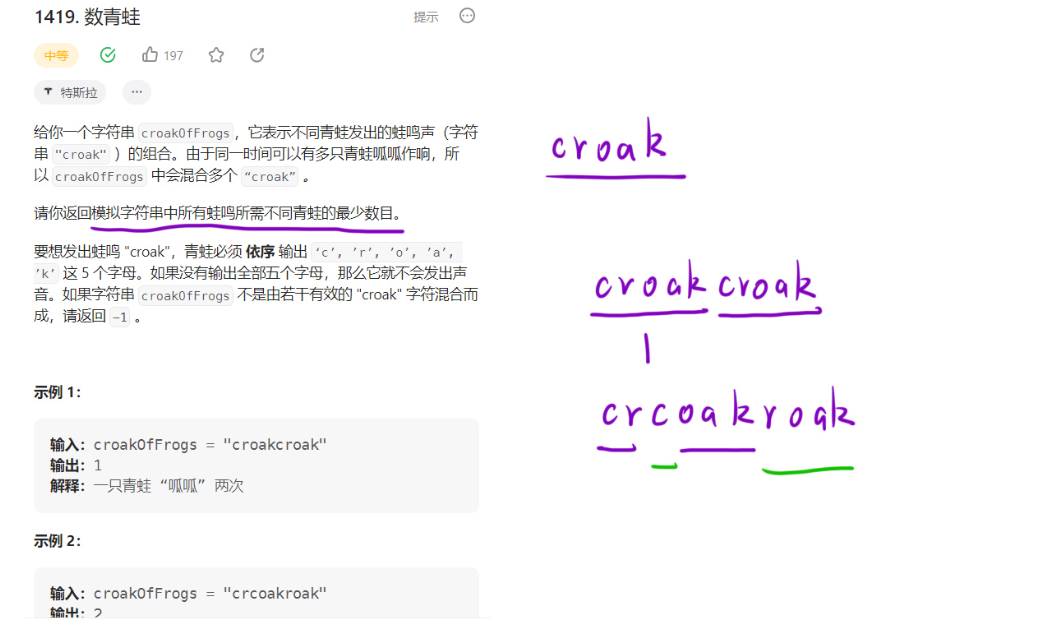
问题背景

题目要求：每只青蛙只能按顺序发出 "c"→"r"→"o"→"a"→"k" 这 5 个字符，且可以重复鸣叫（完成一次 "croak" 后可再次从 "c" 开始）。给定一个字符串 croakOfFrogs，求最少需要多少只青蛙才能发出这个字符串中的所有叫声，若序列无效（如顺序错误或不完整）则返回 -1。

核心思路

1. 鸣叫顺序约束：每只青蛙的叫声必须严格遵循 "c→r→o→a→k" 的顺序，不能跳步（如不能直接从 "c" 到 "o"）。
2. 青蛙复用：当一只青蛙完成一次完整的 "croak"（即发出 "k"）后，可以再次从 "c" 开始新的鸣叫，因此需要考虑复用青蛙以减少总数。
3. 状态跟踪：用一个数组记录每个字符当前的 “未完成状态” 数量，通过状态变化计算所需青蛙数量。

题目解析：

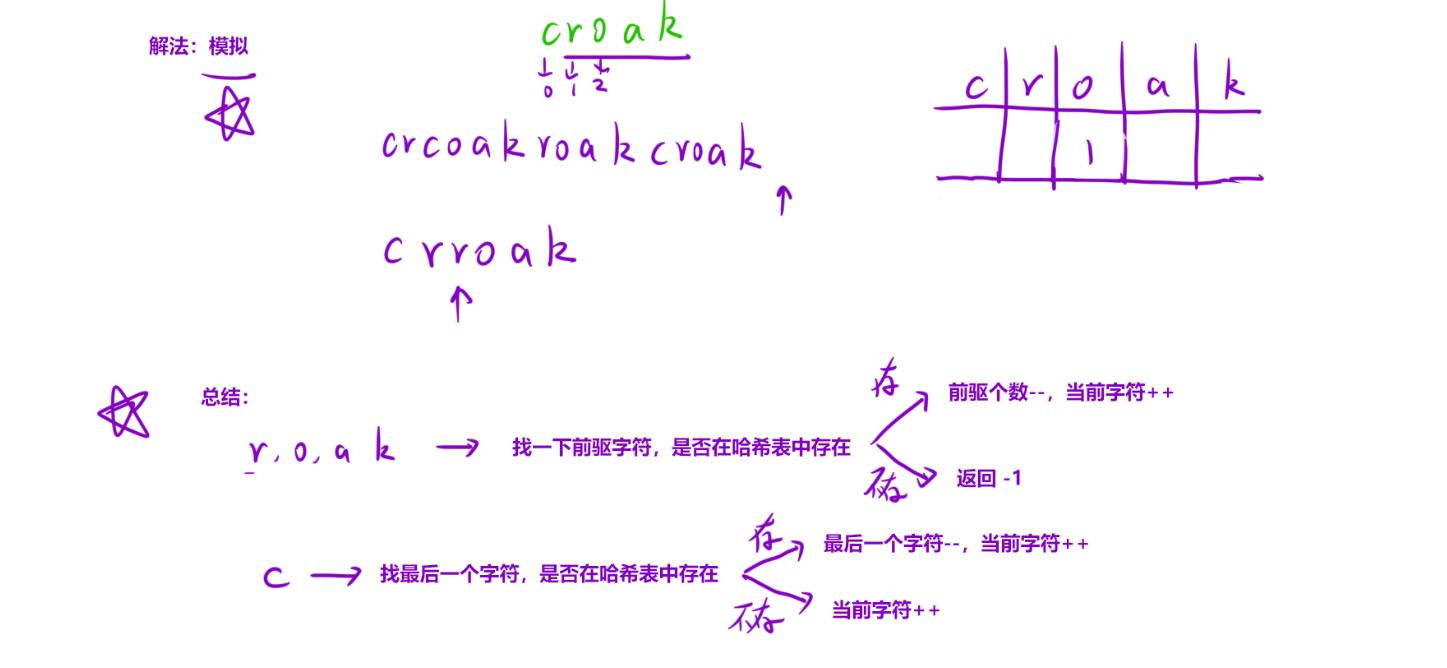
具体逻辑拆解

1. 数据结构设计

• string t = "croak"：定义标准鸣叫顺序。
• vector<int> hash(5)：长度为 5 的数组，分别记录当前处于 "c"、"r"、"o"、"a"、"k" 状态的青蛙数量（即发出了该字符但未继续发出下一个字符的青蛙数量）。
• unordered_map<char, int> index：建立字符到索引的映射（如 'c'→0，'r'→1，...，'k'→4），方便快速查找字符在序列中的位置。

2. 遍历处理每个字符

对输入字符串中的每个字符 ch 进行处理，根据字符类型更新状态：

• 如果是 'c'（序列的第一个字符）：

  • 有两种可能：
    1. 若存在已完成鸣叫的青蛙（hash[4] > 0，即处于 "k" 状态的青蛙），可以复用这只青蛙（让它从 "c" 开始新的鸣叫），因此 hash[4]--（减少一个完成状态的青蛙）。
    2. 若没有可复用的青蛙，需要新增一只青蛙，因此 hash[0]++（增加一个处于 "c" 状态的青蛙）。

• 如果是其他字符（'r'/'o'/'a'/'k'）：

  • 设当前字符在序列中的索引为 i（如 'r' 是 1），则它的前一个字符索引为 i-1（如 'r' 的前一个是 'c'，索引 0）。
  • 必须有青蛙处于前一个状态（hash[i-1] > 0），否则说明顺序错误（如出现 'r' 但没有对应的 'c'），直接返回 -1。
  • 状态转移：将一个青蛙从前一个状态移动到当前状态，即 hash[i-1]-- 且 hash[i]++。

3. 最终校验与结果

• 遍历结束后，需检查是否所有青蛙都完成了鸣叫：
  • 若 hash[0]~hash[3] 中有非 0 值，说明存在未完成的鸣叫（如只有 "cro" 而没有 "ak"），序列无效，返回 -1。
  • 若所有前 4 个状态都为 0，则 hash[4]（处于 "k" 状态的青蛙数量）就是最少需要的青蛙数量（因为每只青蛙最终都会停在 "k" 状态，可复用）。

时间和空间复杂度

• 时间复杂度：O (L)，其中 L 是输入字符串长度，只需遍历一次。
• 空间复杂度：O (1)，仅使用固定大小的数组和映射（与输入长度无关）。