环形链表快慢指针全解析：相遇必然性与多步速追击证明

一、链表中是否有环

        我们在解决链表是否成环问题（https://leetcode.cn/problems/linked-list-cycle/description/）时，一般会选择创建快慢指针，如果在快指针或快指针的下一个节点为空之前，两个指针相遇，则表示成环。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {ListNode* slow=head;ListNode* fast=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(slow==fast){return true;}}return false;
}

二、关于环形链表的思考

假设头结点到slow结点的⻓度为L，环的长度为C，当slow进入环后，fast到slow的距离为N。

（一）为什么快指针走两步，慢指针走一步可以相遇，有没有可能不会相遇？

        

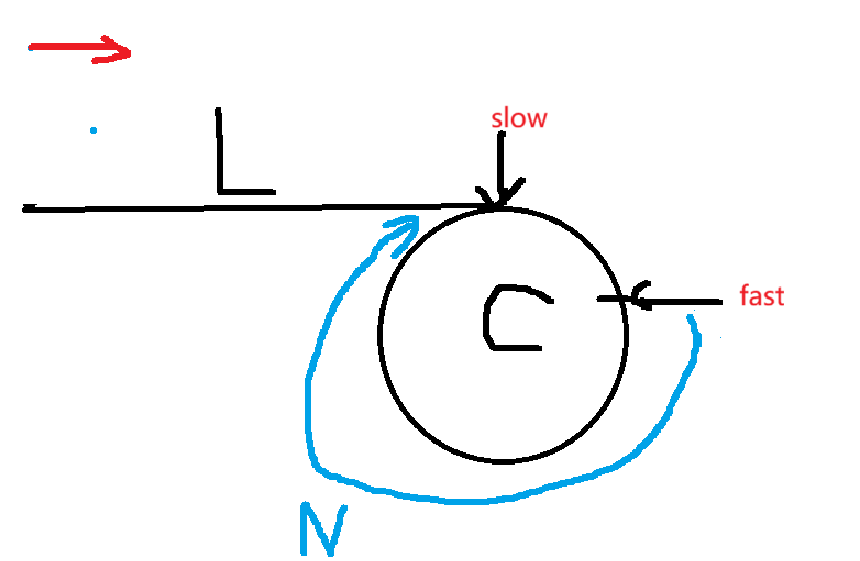
        假设 slow 进入环后，fast 和 slow 距离为 N。我们把每次指针移动分开看，slow 走一步，快慢指针距离变为 N+1；fast 走一步，快慢指针距离变为 N-1。所以快慢指针每移动一次，它们的相对距离会 -1，距离最终必定为 0，因此在带环链表中，慢指针走一步，快指针走两步，快慢指针最终一定会相遇。

（二）快指针一次走3步、4步、……n步可以相遇吗？

        假设快指针一次走3步。根据思考（一）推导过程，可以发现他们的距离每次移动会 -2（如下图）。

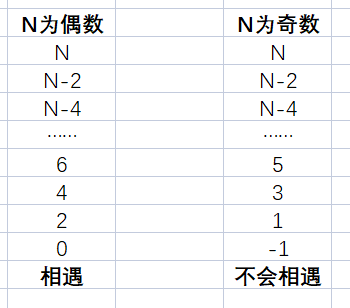
        由图可知，当 N 为偶数时，第一轮会追上；当 N 为奇数时，该轮追不上，进入下一轮，他们的长度变为 C-1。

        所以可以得出以下结论：

1. 如果 N 是偶数，第⼀轮就追上了

2. 如果 N 是奇数 ，第⼀轮追不上，快追上，错过了，距离变成-1，即C-1，进⼊新的⼀轮追击

        （1） C-1如果是偶数，那么下⼀轮就追上了

        （2） C-1如果是奇数， 那么就永远追不上了

总结⼀下，追不上的前提条件：N是奇数，C是偶数。

        但是，N是奇数，C是偶数这种情况会永远存在吗？
        假设，环的周⻓为C，头结点到slow结点的⻓度为L，slow ⾛⼀步，fast ⾛三步，当slow指针⼊环后， slow 和 fast 指针在环中开始进⾏追逐，假设相遇时 fast 指针比 slow 指针多走 x 周。

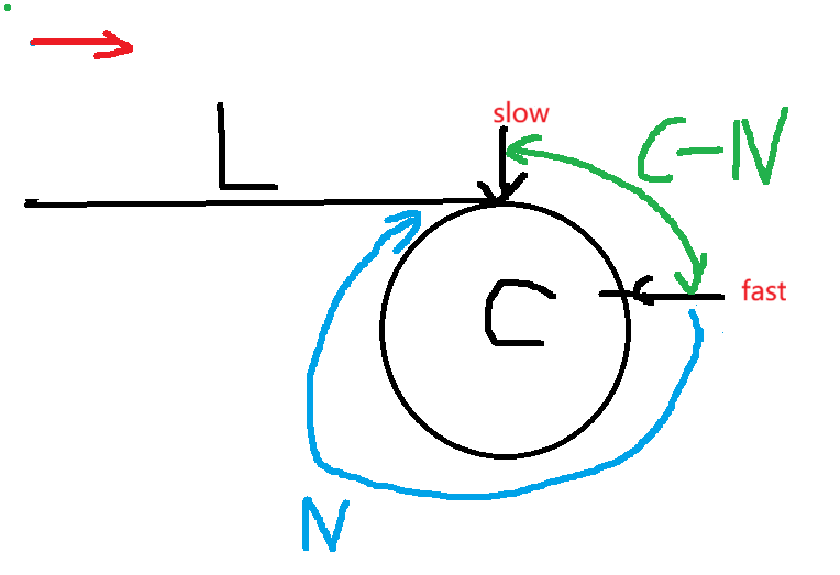
在追逐过程中，快慢指针相遇时走过的路径长度为：

        slow：L

        fast：L+x*C+（C-N）

注：C-N是slow进环时，fast 相对于环入口的距离

        因为慢指针⾛⼀步，快指针要⾛三步，可以得出：3 * 慢指针路程 = 快指针路程

3L =L+x*C+C−N  ->  2L =(x+1)*C −N

因为 2L 一定是偶数，所以有以下两种情况

        （1）偶数=偶数-偶数

        （2）偶数=奇数-奇数

         在上面得出的结论中，如果 N 为偶数第一圈就相遇了；如果 N 为奇数，要满足上方公式（2）的话 (x+1)*C 也必须是奇数，即 C 为奇数。但是 C-1 就是偶数了，还是会相遇。

        因此，上方结论中的“N 是奇数， C 是偶数” 不会永远成立，则快指针一次走3步，最终一定可以相遇。快指针走4、5……最终也会相遇，证明方式同上（也可写代码验证，改变目录一中 fast 指针的变化即可）。