【算法】day17 多维动态规划

1、不同路径

题目：62. 不同路径 - 力扣（LeetCode）

分析：

状态表示：从起点到位置 [i,j] 有 dp[i][j] 种走法。

状态转换方程： 

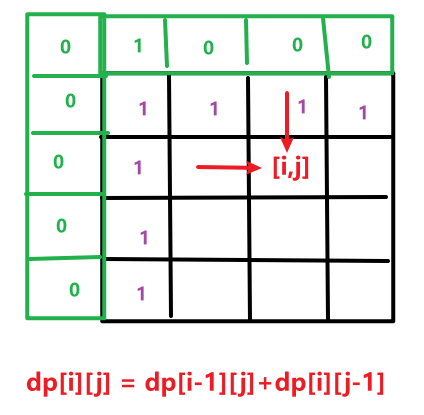
初始化：我们假设 [1,1] 是起点，[0, j]、[i,0] 是虚拟点，用于初始化，根据边界位置推断，只需初始化 dp[0][1]=1。从 i=1、j=1 开始填表，这样可以防止越界。

时间复杂度：O(m*n)；空间复杂度：O(m*n)。

空间优化：O(n)。去掉行的维度。

代码：

class Solution {public int uniquePaths(int m, int n) {int[] dp = new int[n+1];// 初始化dp[1] = 1;// 填表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++)dp[j] = dp[j] + dp[j-1];}return dp[n];}
}

2、最小路径和

题目：64. 最小路径和 - 力扣（LeetCode）

分析：

状态表示：起点到达 [i,j] 位置的最小路径和。

状态转换：

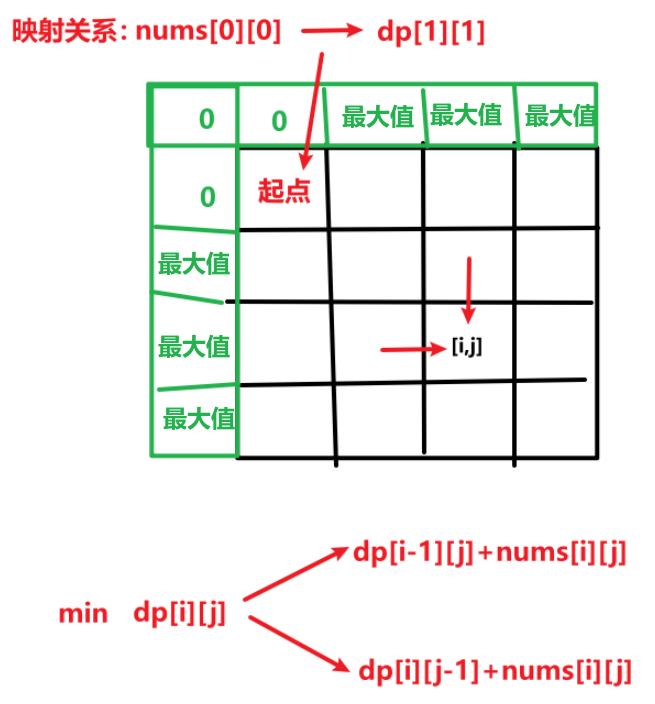
初始化：虚拟节点，从起点映射到 [1,1] 开始填，防止越界。

时间复杂度：O(m*n)，空间复杂度：O(m*n)

空间优化：不能空间优化，因为每一行的初始值不一样，有 0 和最大值两种。

代码：

class Solution {public int minPathSum(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] dp = new int[m+1][n+1];// 初始化for (int i = 2; i <= m; i++) dp[i][0] = Integer.MAX_VALUE;for (int j = 2; j <= n; j++) dp[0][j] = Integer.MAX_VALUE;// 填表for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1];return dp[m][n];}
}

3、最长回文子串

题目：5. 最长回文子串 - 力扣（LeetCode）

分析：首先把所有字串是否是回文子串记录在 dp 表，再根据 dp 表得知哪些子串是回文子串，获取其中最长的长度 max(j-i+1)。

状态表示：dp[i][j] 表示以 i 开头以 j 结尾的子串是否是回文子串。

状态转移方程：

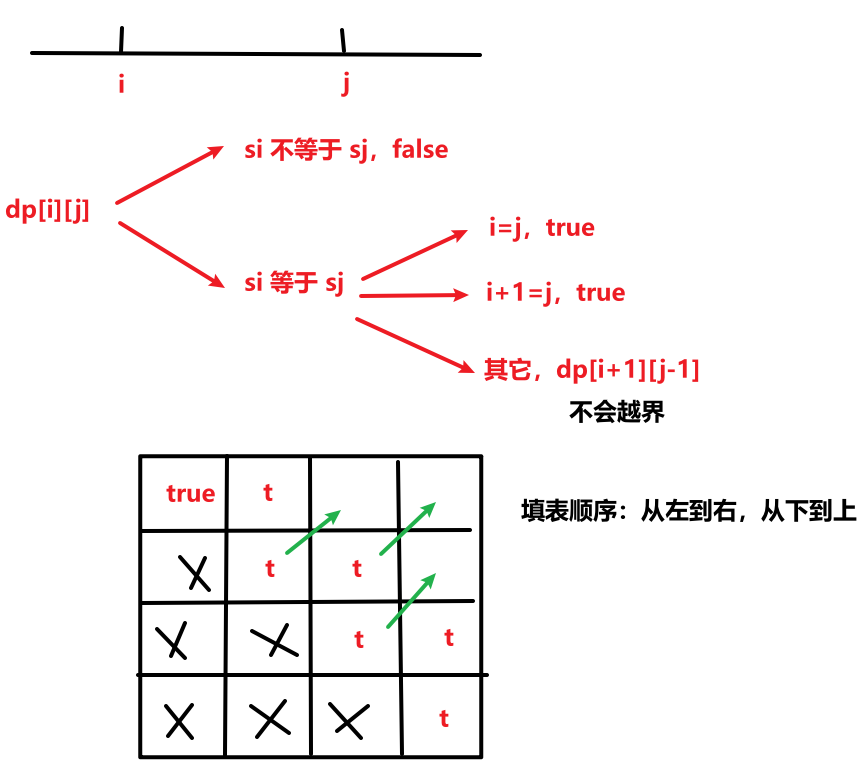
时间复杂度：O(n^2)；空间复杂度：O(n^2)。

代码：

class Solution {public String longestPalindrome(String s) {int n = s.length();char[] chars = s.toCharArray();boolean[][] dp = new boolean[n][n];int maxLen = 0, begin=0;for (int i = n-1; i >= 0; i--) {for (int j = i; j < n; j++) {if (chars[i] != chars[j]) dp[i][j] = false;else {if (i == j || i+1 == j) dp[i][j] = true;else dp[i][j] = dp[i+1][j-1];if (dp[i][j] == true && (j-i+1) > maxLen) {maxLen = j-i+1;begin = i;}}}}return s.substring(begin, begin+maxLen);}
}

4、最长公共子序列

题目：1143. 最长公共子序列 - 力扣（LeetCode）

分析：

状态表示：dp[i][j] 表示字符串 s1 的子串 [0,i]，和 s2 的子串 [0,j] 中的所有最长公共子序列中最长的长度。

状态转移方程：

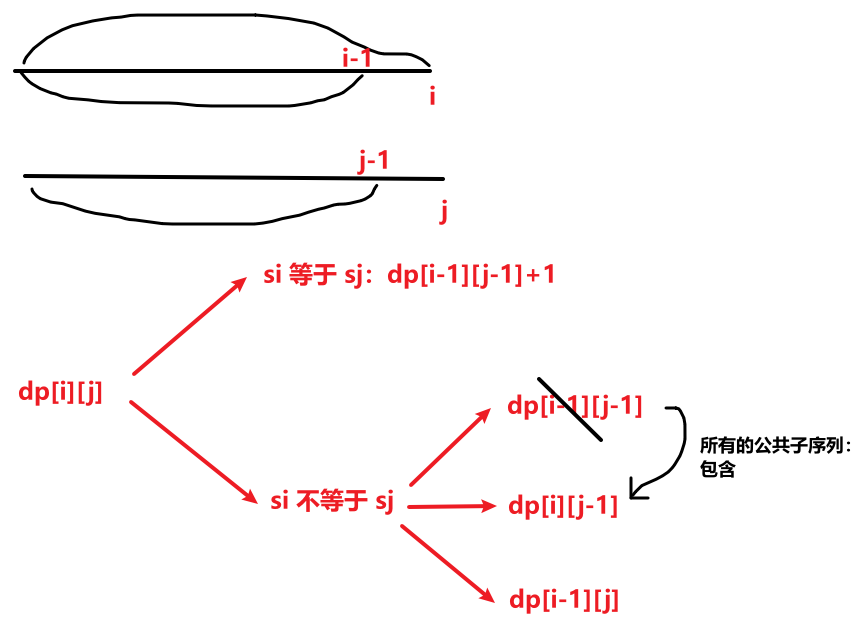
初始化，构造虚拟节点，防止越界：

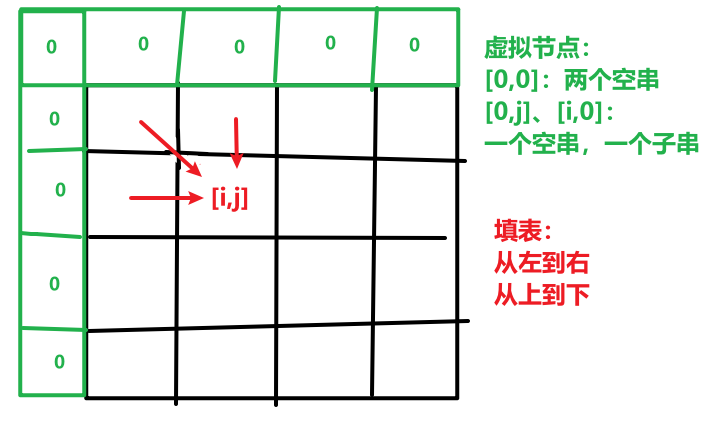
时间复杂度：O(m*n)；空间复杂度：O(m*n)。

代码：

class Solution {public int longestCommonSubsequence(String text1, String text2) {char[] chars1 = text1.toCharArray();char[] chars2 = text2.toCharArray();int m = chars1.length;int n = chars2.length;int[][] dp = new int[m+1][n+1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (chars1[i-1] == chars2[j-1]) dp[i][j] = dp[i-1][j-1]+1;else dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);}}return dp[m][n];}
}

5、编辑距离

题目：72. 编辑距离 - 力扣（LeetCode）

分析：

状态表示：以 i 结尾的单词1转换为以 j 结尾的单词2最少编辑 dp[i][j] 次。

状态转移：

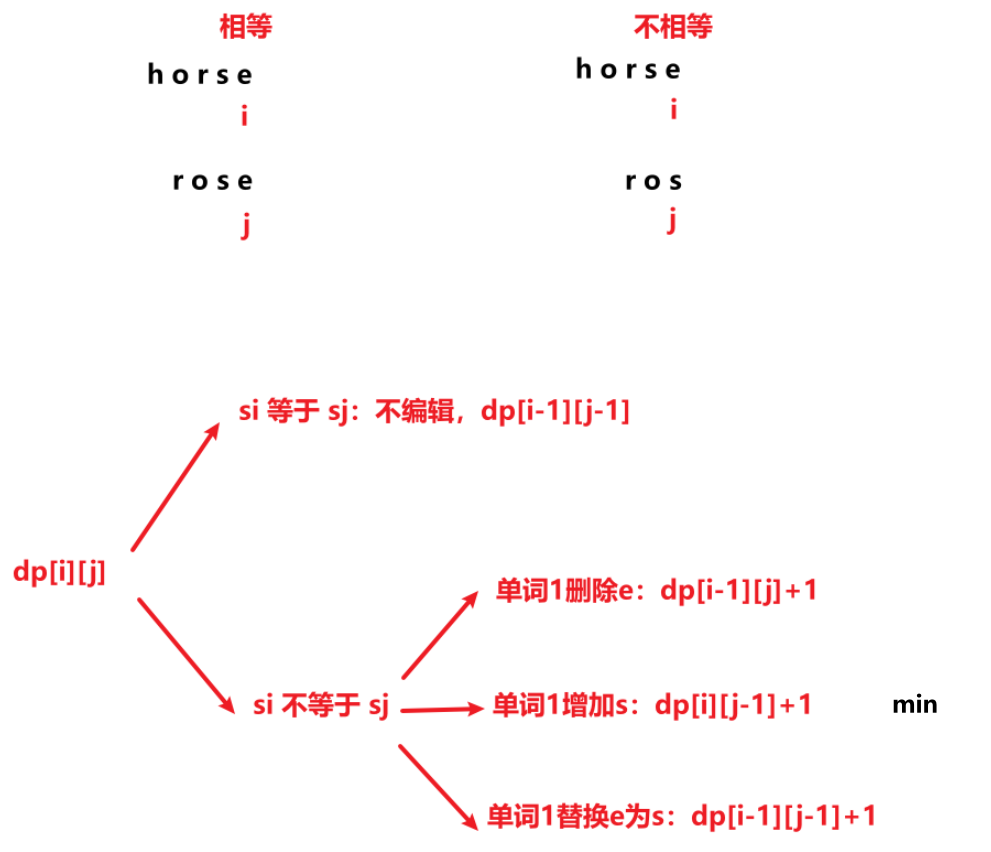
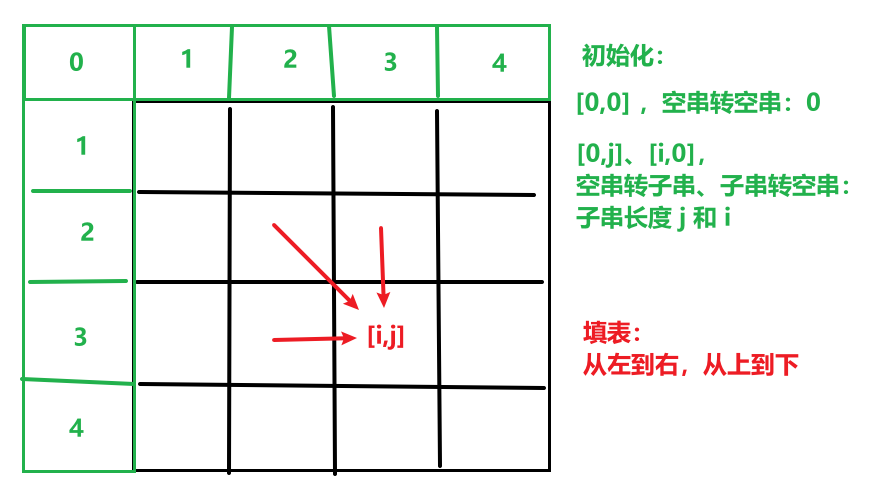
时间复杂度：O(m*n)，空间复杂度：O(m*n)。

代码：

class Solution {public int minDistance(String word1, String word2) {char[] chars1 = word1.toCharArray();char[] chars2 = word2.toCharArray();int m = word1.length();int n = word2.length();int[][] dp = new int[m+1][n+1];for (int i = 1; i <=m; i++) dp[i][0] = i;for (int j = 1; j <=n; j++) dp[0][j] = j;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (chars1[i-1] == chars2[j-1]) dp[i][j] = dp[i-1][j-1];else dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1])) + 1;}}return dp[m][n];}
}