当前位置：首页 > news >正文

基于信号分解的FMCW雷达相互干扰抑制——论文阅读

news 2025/11/10 7:39:34

基于信号分解的FMCW雷达相互干扰抑制

A. Gaur, P. -H. Tseng, K. -T. Feng and S. Srirangarajan, “Signal Decomposition Based Mutual Interference Suppression in FMCW Radars,” in IEEE Open Journal of Vehicular Technology, vol. 6, pp. 2677-2692, 2025, doi: 10.1109/OJVT.2025.3610715.

摘要

随着频率调制连续波（FMCW）雷达在自动驾驶汽车中的应用日益增多，雷达间的相互干扰已成为一个严峻的挑战。这项工作提出了一种新颖的方法（被命名为 VAFER），旨在高效、简洁地抑制FMCW雷达的相互干扰。

该方法的核心流程如下：
首先，使用变分模式分解（VMD） 将接收到的信号分解为多个模式（modes）。接着，利用傅里叶同步压缩变换（FSST） 对这些模式进行时频分析。最后，通过在VMD模式的时频谱上应用一种新提出的基于能量-熵的阈值（energy-entropy-based thresholding） 操作，来重建抑制了干扰的信号。

该方法的有效性通过信干噪比（SINR）、相关系数和检测概率等指标进行了衡量。与现有的干扰抑制方法相比，所提出的VAFER方案在输出SINR方面表现出显著改进，仿真数据至少提高了15.46 dB，实验数据提高了9.87 dB。

I. 引言

FMCW雷达因其在恶劣天气下的鲁棒性、高性价比以及能同时测量距离、角度和速度的能力，已成为高级驾驶辅助系统（ADAS）的首选。然而，随着车辆上雷达数量的增加，雷达间的相互干扰问题变得异常严重。

本文的核心观察在于FMCW雷达信号的特性：

目标信号： 在基带处理中，目标回波表现为单音（tones），即恒定频率的拍频信号。
干扰信号： 来自具有不同线性调频斜率的外部FMCW雷达的干扰，在基带中则表现为线性调频信号（chirp）。

这种强干扰会抬高噪声基底，降低目标回波与背景噪声的可分离性，从而降低检测概率。

现有的干扰抑制方法主要分为三类：

协同方法： 通过修改雷达参数（如相位编码、MAC协议）来避免干扰，但这需要额外的协调单元。
新波形设计： 如跳频、正交噪声波形等，但这可能导致噪声基底增加。
信号处理算法： 这是本文的重点。包括正交投影滤波、矩阵束算法、小波变换、压缩感知（CS）以及基于VMD/EMD的非平稳信号处理技术。

本文的贡献在于提出了一种名为 VAFER 的独特算法，它结合了VMD、FSST和能量-熵重建。该方法利用VMD将信号（目标音调和干扰调频）分解开，然后利用FSST的高时频分辨率特性进行分析，最后通过一种新颖的能量-熵阈值来自动丢弃包含干扰的模式，并重建干净的目标信号。

II. 信号模型与问题阐述

理解本文的关键在于其数学模型，该模型清晰地区分了目标和干扰。

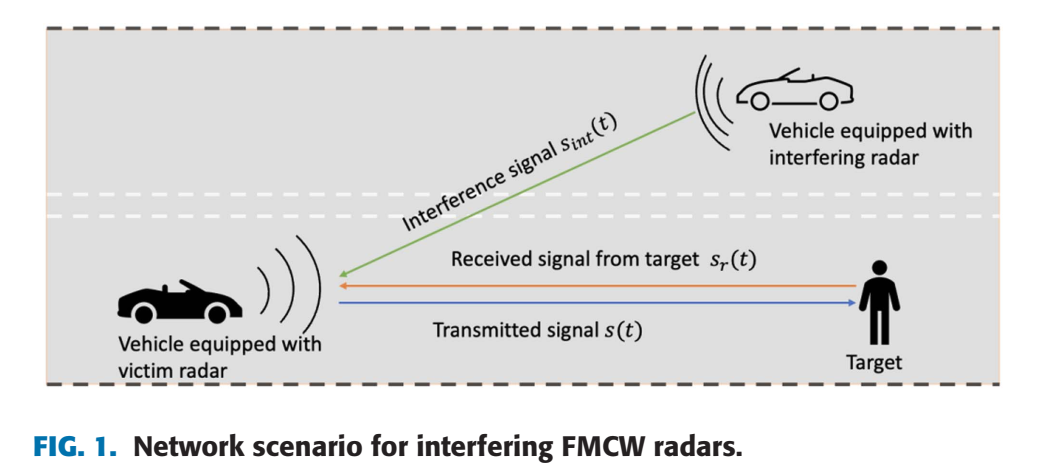
如图1所示，场景中有一个“受害雷达”、一个目标和一个“干扰雷达”。

目标信号模型

发射信号： 受害雷达发射一个归一化的线性调频信号 $s (t)$ ：
$\exp[j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
其中 $f_o$ 是起始频率， $μ=B/T\mu = B/T$ 是调频斜率。
目标回波： 从 $Q$ 个目标反射的回波 $s_r(t)$ 是发射信号的延迟叠加：
$sr(t)=∑q=1Qαqexp⁡[j2π(fo(t−τq)+12μ(t−τq)2)]s_{r}(t) = \sum_{q=1}^{Q}\alpha_{q}\exp[j2\pi(f_{o}(t-\tau_{q}) + \frac{1}{2}\mu(t-\tau_{q})^{2})]$
其中 $αq\alpha_q$ 是复幅度， $τq\tau_q$ 是传播延迟。
去调频（De-chirping）： 接收到的回波 $s_r(t)$ 与发射信号的共轭 $s^*(t)$ 相乘，得到目标拍频信号 $s_b(t)$ ：
$sb(t)=sr(t)⋅s∗(t)=∑q=1Qαqexp⁡[j2π(−foτq−μtτq+μτq22)]s_{b}(t) = s_{r}(t) \cdot s^{*}(t) = \sum_{q=1}^{Q}\alpha_{q}\exp[j2\pi(-f_{o}\tau_{q} - \mu t\tau_{q} + \frac{\mu\tau_{q}^{2}}{2})]$

干扰信号模型

干扰信号： 来自 $M$ 个干扰雷达的信号 $s_{int}(t)$ ，它们具有不同的起始频率 $f_m$ 和调频斜率 $βm\beta_m$ ：
$sint(t)=∑m=1Mexp⁡[j2π(fm(t−τm′)+12βm(t−τm′)2)]s_{int}(t) = \sum_{m=1}^{M}\exp[j2\pi(f_{m}(t-\tau_{m}^{\prime}) + \frac{1}{2}\beta_{m}(t-\tau_{m}^{\prime})^{2})]$
去调频（De-chirping）： 关键在于，这个干扰信号 $s_{int}(t)$ 被受害雷达的 $s^*(t)$ 进行去调频，得到干扰拍频信号 $s_{b,int}(t)$ 。

推导 $sb,int(t)=sint(t)⋅s∗(t)s_{b,int}(t) = s_{int}(t) \cdot s^*(t)$ ，提取时变项，可得（公式5）：
$sb,int(t)=∑m=1MαIexp⁡[j2π((fm−fo−βmτm′)t+12(βm−μ)t2)]s_{b,int}(t) = \sum_{m=1}^{M}\alpha_{I}\exp[j2\pi((f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime})t + \frac{1}{2}(\beta_{m}-\mu)t^{2})]$

问题的核心：瞬时频率

在信号通过低通滤波器（LPF） $h (t)$ 后，总的基带信号 $r~b(t)\tilde{r}_b(t)$ 是目标信号、干扰信号和噪声 $η(t)\eta(t)$ 之和。

本文通过求相位对时间的导数，来分析目标和干扰的瞬时拍频：

目标瞬时频率 $f_b(t)$ (公式9):
$fb(t)=12πddt(phase[sb(t)])=−μτqf_{b}(t) = \frac{1}{2\pi}\frac{d}{dt}(\text{phase}[s_b(t)]) = -\mu\tau_q$
这是一个常数。因此，目标在时频图上表现为水平的直线（单音）。
干扰瞬时频率 $f_{b,int}(t)$ (公式8):
$fb,int(t)=12πddt(phase[sb,int(t)])=(fm−fo−βmτm′)+(βm−μ)tf_{b,int}(t) = \frac{1}{2\pi}\frac{d}{dt}(\text{phase}[s_{b,int}(t)]) = (f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime}) + (\beta_{m}-\mu)t$
这是一个随时间 $t$ 线性变化的频率（假设 $βm≠μ\beta_m \neq \mu$ ）。因此，干扰在时频图上表现为倾斜的直线（Chirp）。

本文的目标就是利用这种时频特性的根本差异（目标=平稳单音 vs. 干扰=非平稳Chirp），设计一个信号处理方案来分离它们。

III. 提出的VAFER方案

VAFER 算法是本文的核心，它由三个步骤组成。

A. 变分模式分解 (VMD)

第一步是分解信号。VMD 是一种自适应信号分解技术，它将多分量信号 $r~b(t)\tilde{r}_b(t)$ 分解为 $K$ 个窄带的变分模式函数（VMFs） $u_k(t)$ 。选择VMD是因为它能将不同的单音频率（目标信号）映射到各自独立的模式中。与EMD等方法相比，VMD对噪声更鲁棒，不易产生模式混叠。

VMD的数学原理是通过求解一个约束变分问题来实现分解。其目标是最小化所有模式的估计带宽之和，约束条件是所有模式相加必须等于原始信号。

VMD的代价函数 (公式10) 如下：
$min⁡uk,ωk{∑k=1K∥∂t[(δ(t)+jπt)∗uk(t)]e−jωkt∥22}\min_{{u_k}, {\omega_k}} \left\{ \sum_{k=1}^{K} \left\| \partial_t \left[ \left(\delta(t) + \frac{j}{\pi t}\right) * u_k(t) \right] e^{-j\omega_k t} \right\|_2^2 \right\}$
$s.t.∑k=1Kuk(t)=r~b(t)\text{s.t.} \sum_{k=1}^{K} u_k(t) = \tilde{r}_{b}(t)$

这个公式的内部项 $[(δ(t)+j/(πt))∗uk(t)][(\delta(t) + j/(\pi t)) * u_k(t)]$ 是通过希尔伯特变换计算模式 $u_k$ 的解析信号。 $e−jωkte^{-j\omega_k t}$ 将其频谱移至中心频率 $ωk\omega_k$ 。 $∂t\partial_t$ （导数）和 $L_2$ 范数共同估计该模式的带宽。为了求解，通过引入二次惩罚因子 $α\alpha$ 和拉格朗日乘子 $λ(t)\lambda(t)$ （公式11），将问题转为无约束优化。然后使用交替方向乘子法（ADMM）在频域中迭代更新 $u^k(ω)\hat{u}_k(\omega)$ 和 $ωk\omega_k$ （公式12, 13），直至收敛。

B. 傅里叶同步压缩变换 (FSST)

分解得到 $K$ 个 VMFs 后，第二步是对每一个 $u_k$ 进行时频分析。

之所以选择FSST而不是常规的STFT，是因为FSST 是一种时频重分配技术，它能将STFT的能量“压缩”到信号的瞬时频率上，从而极大地锐化时频表示。

FSST的效果非常关键：

对于包含目标（单音）的VMF，FSST会将其表示为一条非常清晰、能量集中的水平线。
对于包含干扰（Chirp或噪声）的VMF，FSST会将其表示为模糊的、能量分散的“噪声团”。

FSST的数学原理首先计算 $u_k$ 的STFT（公式16），然后计算STFT谱的质心（瞬时频率） $ω^uk(t,ω)\hat{\omega}_{u_{k}}(t,\omega)$ ，最后将能量从 $ω\omega$ 重新分配到 $ω^uk\hat{\omega}_{u_k}$ ，得到 $Uk(t,ω)U_k(t, \omega)$ （公式18）。

C. 能量-熵阈值与重建

第三步是自动区分“好”模式（目标）和“坏”模式（干扰）。本文提出使用维纳熵（Wiener entropy），它是衡量频谱平坦度（或“尖峰度”）的指标。

根据本文的逻辑，目标模式在FSST谱中表现为单音，能量集中，频谱“尖锐”；而干扰模式能量分散，频谱更“平坦”。

维纳熵计算 (公式19) 如下：
$W(Uk(t,ω))=[∏i=1N∏j=1F∣Uk(ti,ωj)∣2]1/NF1NF∑i=1N∑j=1F∣Uk(ti,ωj)∣2W(U_{k}(t,\omega))=\frac{[\prod_{i=1}^{N}\prod_{j=1}^{F}|U_{k}(t_{i},\omega_{j})|^{2}]^{1/NF}}{\frac{1}{NF}\sum_{i=1}^{N}\sum_{j=1}^{F}|U_{k}(t_{i},\omega_{j})|^{2}}$
这是FSST功率谱的几何平均值与算术平均值之比。

为了使阈值 $TβT_{\beta}$ 更鲁棒，本文使用每个模式的能量 $Ek=∫∣uk(t)∣2dtE_k = \int |u_k(t)|^2 dt$ 作为权重，计算维纳熵的加权平均值，从而得到一个动态阈值 (公式20)：
$Tβ=∑k=1KEk⋅W(Uk(t,ω))∑k=1KEkT_{\beta}=\frac{\sum_{k=1}^{K}E_{k}\cdot W(U_{k}(t,\omega))}{\sum_{k=1}^{K}E_{k}}$

最后，进行信号重建（公式22, 23）。保留所有维纳熵 $W(U_k)$ 大于等于 $TβT_{\beta}$ 的模式，并丢弃其余的干扰模式。将保留的模式通过逆FSST相加，即可重建出干净的信号 $r^b(t)\hat{r}_b(t)$ 。

IV. 性能评估

本节通过仿真和实验数据，将VAFER与ANC、SPARKLE、WD、Bi- $l_1$ 和VAFER-STFT（使用STFT代替FSST的变体）进行比较。

仿真结果

仿真设置了4个目标（10, 16, 30, 50米）和2个干扰源。

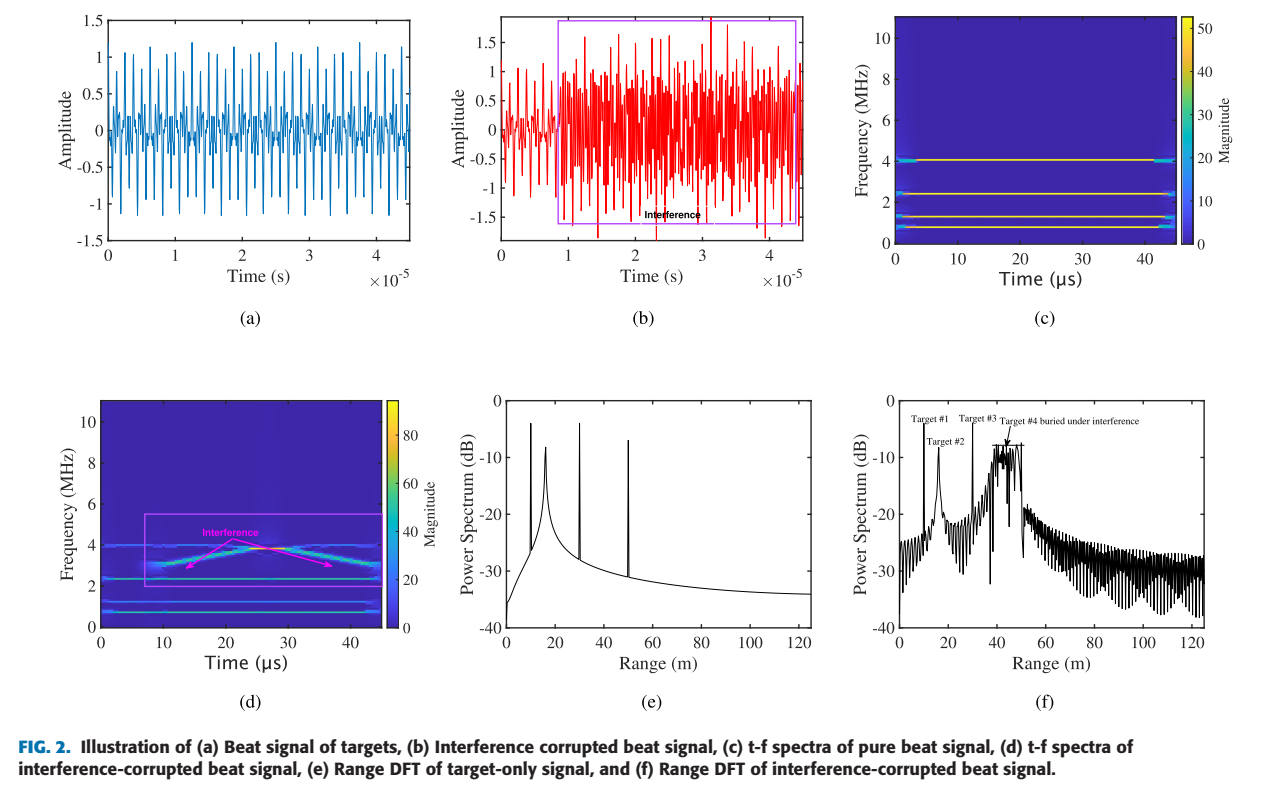
图 2 显示了干扰的严重影响。
- (a) 是纯净的目标信号时域波形。
- © 和 (e) 是纯净信号的时频谱（4条清晰的水平线）和距离DFT（4个尖锐的峰值）。
- (b) 是被干扰污染后的时域波形。
- (d) 和 (f) 是受干扰信号的时频谱和距离DFT。在时频图 (d) 中，目标线被干扰（倾斜的条纹）所掩盖。在距离DFT (f) 中，噪声基底被大幅抬高，导致50米处的第4个目标（Target #4）完全被干扰淹没。

接下来展示VAFER算法的中间步骤。

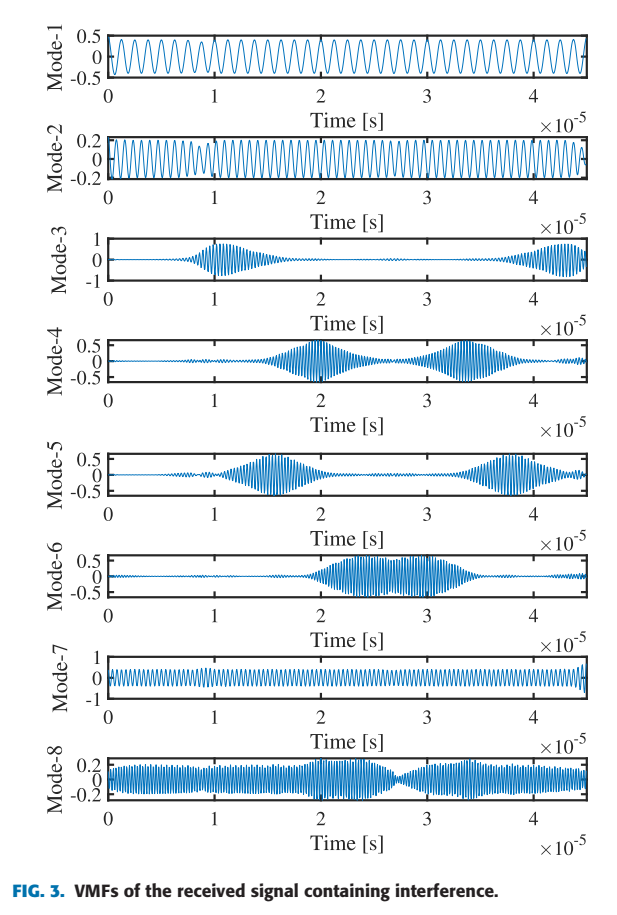
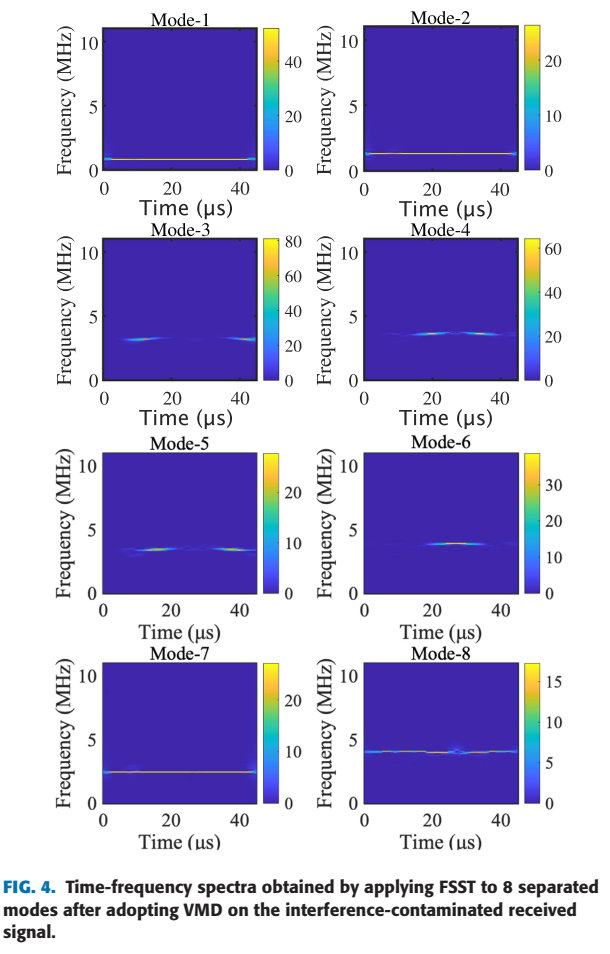
图 3 和图 4 展示了VAFER的效果。
- VMD（图3）： 信号被分解为8个模式。肉眼可见，模式1, 2, 7, 8 是平稳的正弦波（代表4个目标），而模式3, 4, 5, 6 是非平稳的（代表干扰）。
- FSST（图4）： 目标模式（1, 2, 7, 8）被FSST锐化为极其清晰、能量集中的水平线。而干扰模式（3, 4, 5, 6）则呈现为能量分散的“污迹”。这种巨大的差异使得基于熵的阈值分离变得非常容易且可靠。

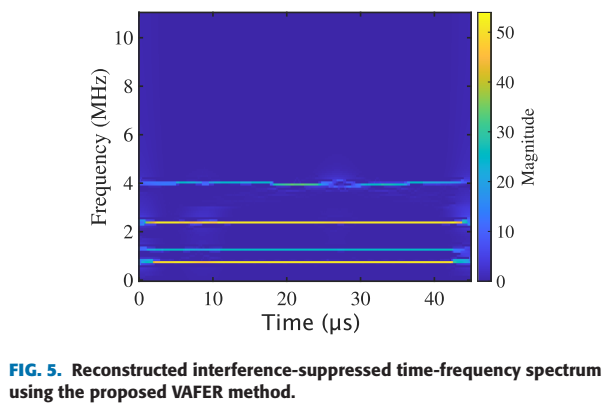
图 5 显示了重建后的时频谱。干扰污迹被完全去除，只留下4条清晰的目标线，证明干扰模式被成功丢弃。

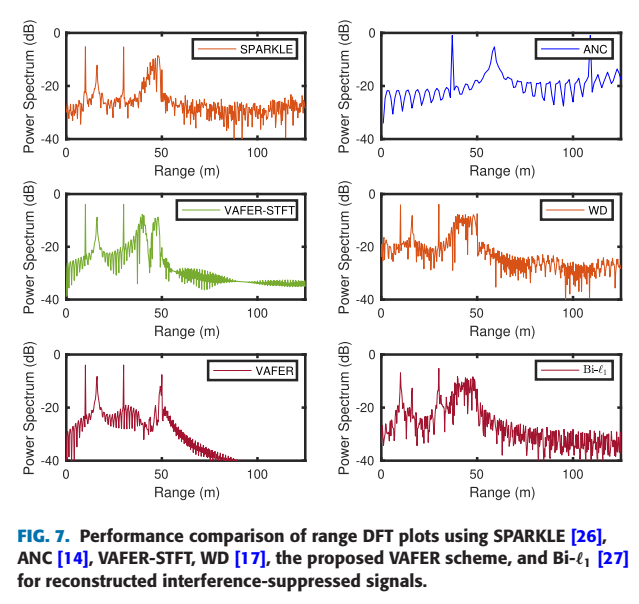
图 7 是一维距离像的关键性能对比。
- ANC、WD、SPARKLE、Bi- $l_1$ 和VAFER-STFT 方法的距离像中，均存在不同程度的残留干扰或噪声基底抬高。
- VAFER（左下角）的距离像中，噪声基底被显著压低，并且之前在图2(f)中被淹没的50米处目标被清晰地检测出来，峰值锐利。

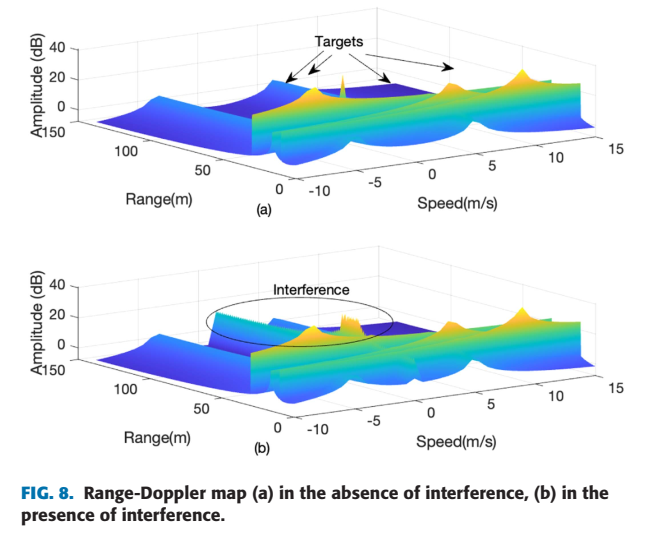
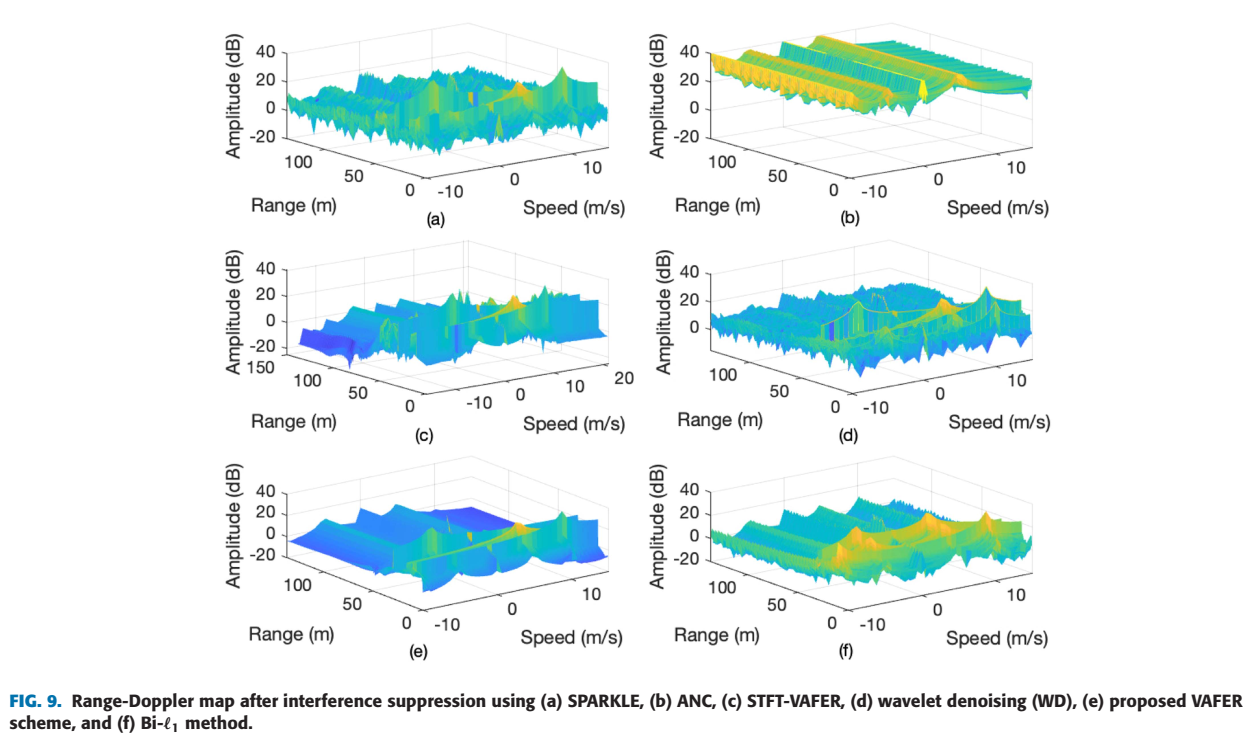
图 8 和图 9 展示了对移动目标（距离-多普勒）的处理效果。
- 图8(a)是纯净的R-D图，(b)显示在原始干扰下，位于（50米, 0米/秒）的静止目标被干扰完全覆盖。
- 图9中，(a) SPARKLE、(b) ANC、© VAFER-STFT、(d) WD、(f) Bi- $l_1$ 均未能有效恢复该目标。
- VAFER（图9(e)）再次展示了其优越性，干扰被完全抑制，所有4个目标在R-D图上都清晰可见。

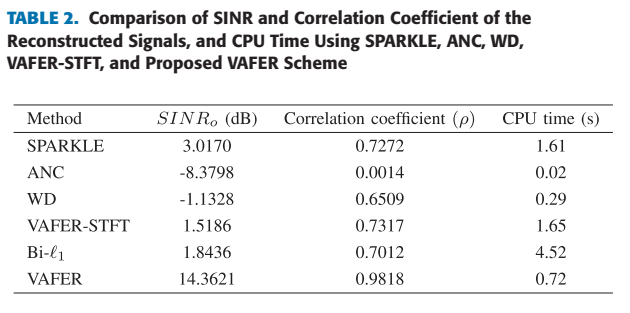
量化结果（表2）： VAFER 取得了最高的 $SINR_O$ （14.3621 dB）和相关系数 $ρ\rho$ （0.9818）。

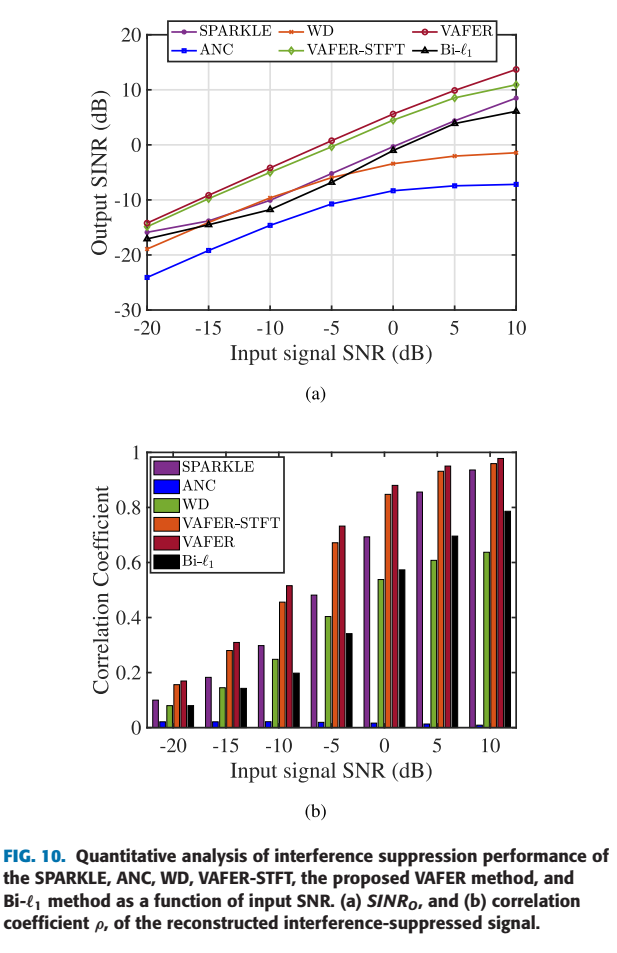
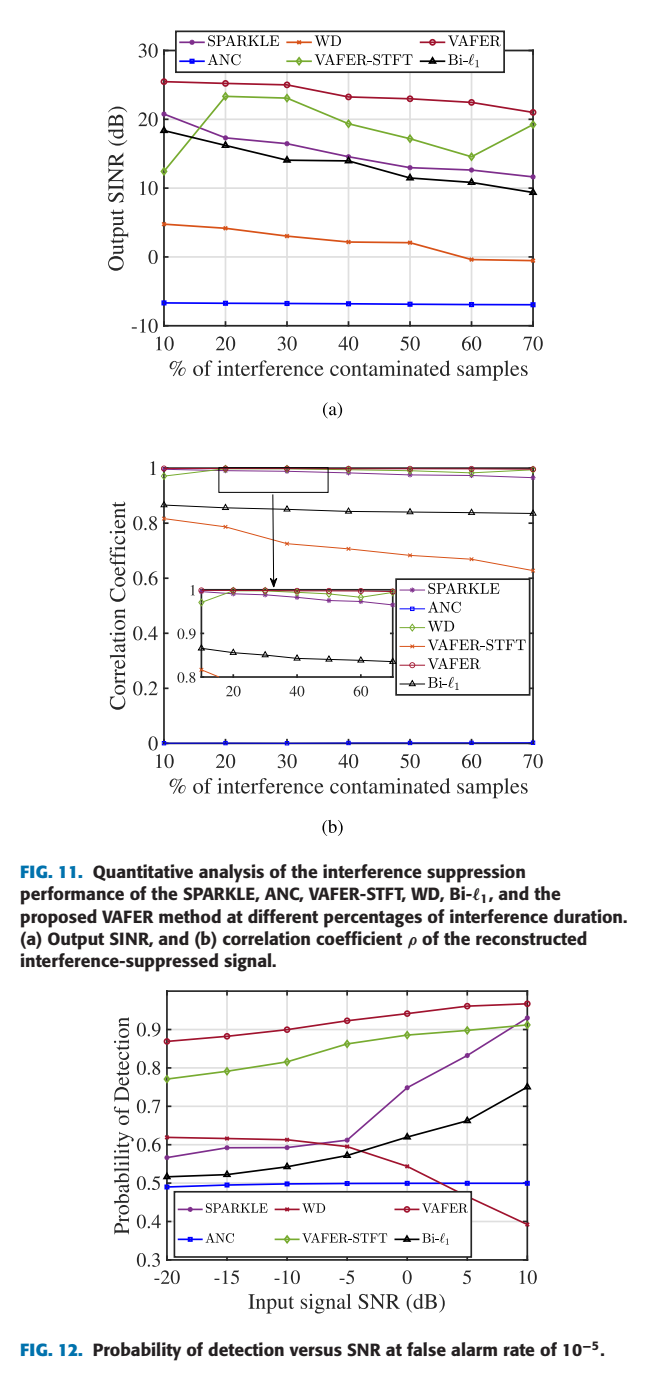
图 10, 11, 12 的鲁棒性分析表明，在不同的输入SNR和不同的干扰污染比例下，VAFER（图例中的VAFER线，通常是红色或紫色）的性能始终全面优于其他所有方法。

实验结果

图 13 显示了实验设置，使用来自真实场景的公开数据。目标是一辆以15米/秒驶近的汽车，干扰源在2米处。

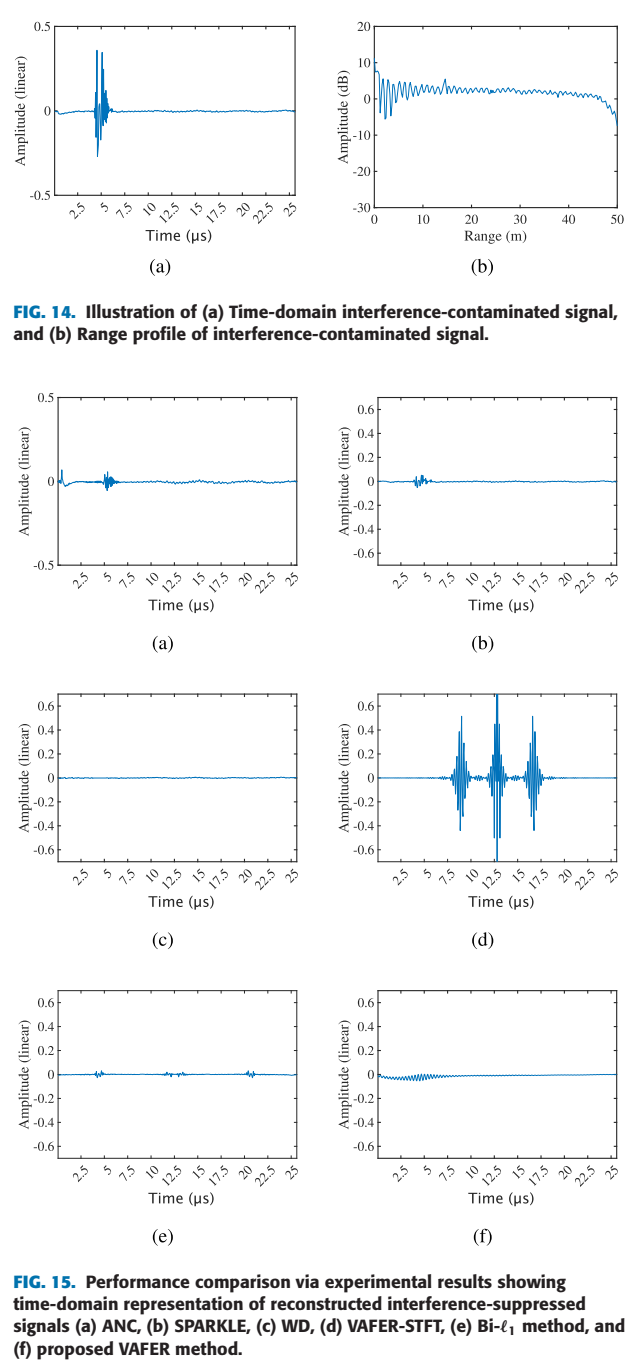
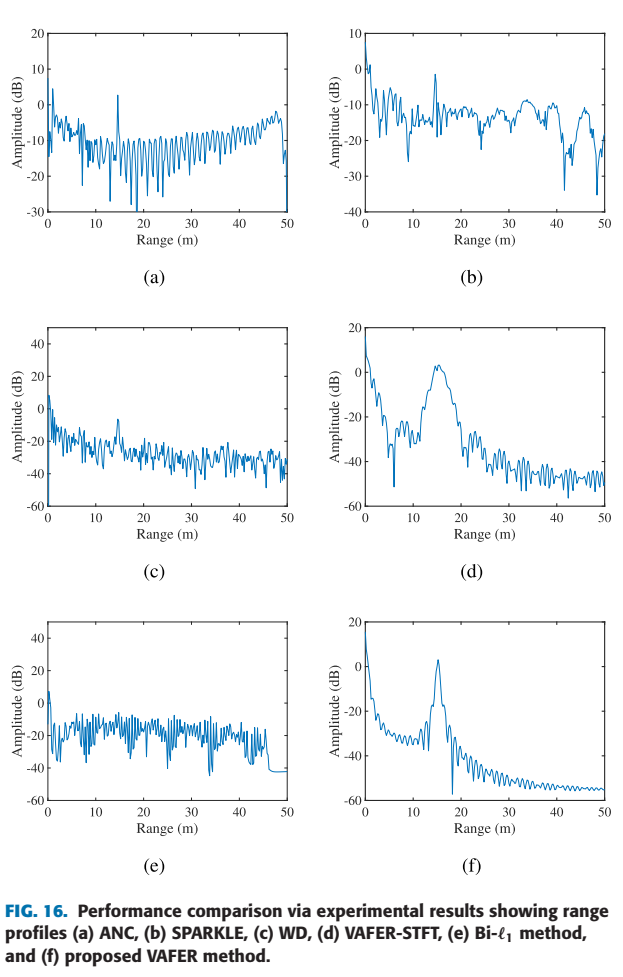
图 14, 15, 16 是实验数据的对比。
- 图14(b)是原始距离剖面，目标（应在14.8米）被噪声淹没，无法辨识。
- 图16（关键对比）：
  - (a) ANC、(b) SPARKLE、(e) Bi- $l_1$ 不仅未能清晰检测目标，还在2米处（干扰源位置）产生了虚假目标峰。
  - © WD 导致目标峰值幅度过低，这归因于信号失真。
  - (d) VAFER-STFT 几乎无效，干扰依然存在。
  - (f) VAFER： 结果非常干净。干扰和虚假目标被完全抑制，在14.8米处清晰地显示了唯一的真实目标峰值。
量化结果（实验）： 原始SINR为2.94 dB。VAFER方法将SINR提高到12.81 dB，净增益为 9.87 dB，显著优于所有其他方法。

V. 结论

本文提出了一种基于VMD和FSST的FMCW雷达干扰抑制方法——VAFER。该方法的核心是利用VMD将信号分解为包含“单音目标”和“调频干扰”的模式，然后利用FSST的锐化时频表示，最后通过一个新颖的能量-熵阈值自动分离并剔除干扰模式。

仿真和真实实验数据均证实，VAFER方案在提高输出SINR和相关系数方面，性能显著优于多种现有的先进算法，能够有效抑制干扰且不对目标信号造成可观察的性能下降。

附录：关键推导

论文在第二节（II. 信号模型）中给出了目标和干扰瞬时频率的最终表达式（公式8和9），但省略了推导过程。这个推导是理解本文核心（目标=单音 vs 干扰=Chirp）的基石。

1. 目标拍频信号 (Beat Signal) 及其瞬时频率

受害雷达发射信号 $s (t)$ (忽略幅度) :
$\exp[j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
其共轭为 $s∗(t)=exp⁡[−j2π(fot+12μt2)]s^*(t) = \exp[-j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
从目标 $q$ 返回的回波 $s_r(t)$ (延迟 $τq\tau_q$ ) :
$sr(t)=s(t−τq)=exp⁡[j2π(fo(t−τq)+12μ(t−τq)2)]s_r(t) = s(t-\tau_q) = \exp[j2\pi(f_{o}(t-\tau_{q}) + \frac{1}{2}\mu(t-\tau_{q})^{2})]$
去调频 (De-chirping) ，将 $s_r(t)$ 与 $s^*(t)$ 混频:
$sb(t)=sr(t)⋅s∗(t)s_b(t) = s_r(t) \cdot s^*(t)$
$sb(t)=exp⁡[j2π(fo(t−τq)+12μ(t−τq)2)]⋅exp⁡[−j2π(fot+12μt2)]s_b(t) = \exp[j2\pi(f_{o}(t-\tau_{q}) + \frac{1}{2}\mu(t-\tau_{q})^{2})] \cdot \exp[-j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
合并指数项 ，相位 $Φb(t)\Phi_b(t)$ 为 $2π2\pi$ 乘以内部各项之和:
$Φb(t)=2π[(fot−foτq)+12μ(t2−2tτq+τq2)−(fot+12μt2)]\Phi_b(t) = 2\pi [ (f_{o}t - f_{o}\tau_q) + \frac{1}{2}\mu(t^2 - 2t\tau_q + \tau_q^2) - (f_o t + \frac{1}{2}\mu t^2) ]$
化简相位 :
- $f_o t$ 与 $f_o t$ 抵消。
- $12μt2\frac{1}{2}\mu t^2$ 与 $−12μt2-\frac{1}{2}\mu t^2$ 抵消。
- 剩余项为: $Φb(t)=2π[−foτq−μtτq+12μτq2]\Phi_b(t) = 2\pi [ -f_{o}\tau_q - \mu t\tau_q + \frac{1}{2}\mu\tau_q^2 ]$
- 这与论文中的公式 (3) 完全一致。
计算瞬时频率 $f_b(t)$ ：
瞬时频率是相位对时间的导数除以 $2π2\pi$ 。
$fb(t)=12πdΦb(t)dt=12πddt[2π(−foτq−μtτq+12μτq2)]f_b(t) = \frac{1}{2\pi} \frac{d\Phi_b(t)}{dt} = \frac{1}{2\pi} \frac{d}{dt} [ 2\pi ( -f_{o}\tau_q - \mu t\tau_q + \frac{1}{2}\mu\tau_q^2 ) ]$
求导 :
- $−foτq-f_o \tau_q$ 是常数，导数为 0。
- $12μτq2\frac{1}{2}\mu\tau_q^2$ 是常数，导数为 0。
- $−μtτq-\mu t\tau_q$ 对 $t$ 的导数为 $−μτq-\mu\tau_q$ 。
$fb(t)=−μτqf_b(t) = -\mu\tau_q$

结论： 目标拍频信号的瞬时频率是一个常数 (与论文公式9一致)，仅取决于调频斜率 $μ\mu$ 和延迟 $τq\tau_q$ （即距离）。这就是“单音”的来源。

2. 干扰拍频信号 (Beat Signal) 及其瞬时频率

干扰信号 $s_{int}(t)$ (来自干扰雷达，斜率 $βm\beta_m$ ，延迟 $τm′\tau_m'$ ):
$sint(t)=exp⁡[j2π(fm(t−τm′)+12βm(t−τm′)2)]s_{int}(t) = \exp[j2\pi(f_{m}(t-\tau_{m}^{\prime}) + \frac{1}{2}\beta_{m}(t-\tau_{m}^{\prime})^{2})]$
受害雷达发射信号共轭 $s^*(t)$ (斜率 $μ\mu$ ):
$s∗(t)=exp⁡[−j2π(fot+12μt2)]s^*(t) = \exp[-j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
去调频，将 $s_{int}(t)$ 与 $s^*(t)$ 混频:
$sb,int(t)=sint(t)⋅s∗(t)s_{b,int}(t) = s_{int}(t) \cdot s^*(t)$
$sb,int(t)=exp⁡[j2π(fm(t−τm′)+12βm(t−τm′)2)]⋅exp⁡[−j2π(fot+12μt2)]s_{b,int}(t) = \exp[j2\pi(f_{m}(t-\tau_{m}^{\prime}) + \frac{1}{2}\beta_{m}(t-\tau_{m}^{\prime})^{2})] \cdot \exp[-j2\pi(f_{o}t + \frac{1}{2}\mu t^{2})]$
合并指数项，相位 $Φint(t)\Phi_{int}(t)$ 为 $2π2\pi$ 乘以内部各项之和:
$Φint(t)=2π[(fmt−fmτm′)+12βm(t2−2tτm′+(τm′)2)−(fot+12μt2)]\Phi_{int}(t) = 2\pi [ (f_{m}t - f_{m}\tau_m') + \frac{1}{2}\beta_{m}(t^2 - 2t\tau_m' + (\tau_m')^2) - (f_o t + \frac{1}{2}\mu t^2) ]$
按 $t$ 的幂次重新组合相位:
- $t^2$ 项: $(12βm−12μ)t2=12(βm−μ)t2(\frac{1}{2}\beta_m - \frac{1}{2}\mu)t^2 = \frac{1}{2}(\beta_m - \mu)t^2$
- $t$ 项: $(fm−βmτm′−fo)t(f_m - \beta_m \tau_m' - f_o)t$
- 常数项: $(−fmτm′+12βm(τm′)2)(-f_m \tau_m' + \frac{1}{2}\beta_m (\tau_m')^2)$
$Φint(t)=2π[12(βm−μ)t2+(fm−fo−βmτm′)t+Constants]\Phi_{int}(t) = 2\pi [ \frac{1}{2}(\beta_{m}-\mu)t^{2} + (f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime})t + \text{Constants} ]$
- 这与论文中的公式 (5), (122), (127) 的相位项完全一致。
计算瞬时频率 $f_{b,int}(t)$ :
$fb,int(t)=12πdΦint(t)dt=12πddt[2π(12(βm−μ)t2+(fm−fo−βmτm′)t+…)]f_{b,int}(t) = \frac{1}{2\pi} \frac{d\Phi_{int}(t)}{dt} = \frac{1}{2\pi} \frac{d}{dt} [ 2\pi ( \frac{1}{2}(\beta_{m}-\mu)t^{2} + (f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime})t + \dots ) ]$
求导:
- 常数项导数为 0。
- $t$ 项的导数为 $(fm−fo−βmτm′)(f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime})$ 。
- $t^2$ 项的导数为 $(βm−μ)t(\beta_m - \mu)t$ 。
$fb,int(t)=(fm−fo−βmτm′)+(βm−μ)tf_{b,int}(t) = (f_{m}-f_{o}-\beta_{m}\tau_{m}^{\prime}) + (\beta_{m}-\mu)t$

结论： 干扰拍频信号的瞬时频率是一个关于时间 $t$ 的线性函数 (与论文公式8一致)。它的频率随时间变化，其变化的斜率（调频斜率）为 $(βm−μ)(\beta_m - \mu)$ 。这就是“Chirp”的来源。