【数据结构】单调栈（模板 + 练习）

一、单调栈

1. 什么是单调栈

单调栈，顾名思义，就是具有单调性的栈。它依旧是一个栈结构，只不过里面存储的数据是递增或者递减的。这种结构是很容易实现的，如下面的代码。

注：我们这里说的递增和递减是严格递增和严格递减。

#include <iostream>
#include <stack>using namespace std;const int N = 3e6 + 10;
int a[N], n;// 遍历 a 数组, 往栈中放元素, 保证栈中的元素是单增或单减的
// 维护一个单调递增的栈 
void test1()
{stack<int> st;// 遍历 a 数组for(int i = 1; i <= n; i++){// 现在要放 a[i], 如果栈不空并且栈顶元素大于等于 a[i], 就把栈顶元素出栈// 直到栈顶元素小于 a[i]while(st.size() && st.top() >= a[i]) st.pop();// 之后再把 a[i] 压栈st.push(a[i]);}// 通过这样的 while 循环, 就可以保证无论什么时候栈中的元素都是递增的
}// 维护一个单调递减的栈 
void test2()
{stack<int> st; for(int i = 1; i <= n; i++){// 现在要放 a[i], 如果栈不空并且栈顶元素小于等于 a[i], 就把栈顶元素出栈// 直到栈顶元素小于 a[i]while(st.size() && st.top() <= a[i]) st.pop();// 之后再把 a[i] 压栈st.push(a[i]);}// 通过这样的 while 循环, 就可以保证无论什么时候栈中的元素都是递减的
}

---

2. 单调栈解决的问题

这样去维护一个单调栈的意义是什么？

单调栈能帮助我们解决以下四个问题，在一个数组中：

• 寻找当前元素左侧，离它最近，并且比它大的元素在哪；

• 寻找当前元素左侧，离它最近，并且比它小的元素在哪；

• 寻找当前元素右侧，离它最近，并且比它大的元素在哪；

• 寻找当前元素右侧，离它最近，并且比它小的元素在哪。

虽然是四个问题，但是原理是一致的。因此，只要解决一个，举⼀反三就可以解决剩下的几个。

我们首先来看单调栈是如何解决第一个问题的：寻找当前元素左侧，离它最近，并且比它大的元素在哪。

从左往右遍历元素，构造一个单调递减的栈。当 while 循环弹栈完成后插入当前位置的元素的时：

• 如果栈为空，则左侧不存在比当前元素大的元素；

• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

注意，因为我们要找的是最终结果的位置。因此，栈里面存的是每个元素的下标。

第二个问题：寻找当前元素左侧，离它最近，并且比它小的元素在哪。

从左往右遍历元素，构造一个单调递增的栈。当 while 循环弹栈完成后插入当前位置的元素的时：

• 如果栈为空，则左侧不存在比当前元素小的元素；

• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

注意，因为我们要找的是最终结果的位置。因此，栈里面存的是每个元素的下标。

第三个问题：寻找当前元素右侧，离它最近，并且比它大的元素在哪。

从右往左遍历元素，构造一个单调递减的栈。当 while 循环弹栈完成后插入当前位置的元素的时：

• 如果栈为空，则右侧不存在比当前元素大的元素；

• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

注意，因为我们要找的是最终结果的位置。因此，栈里面存的是每个元素的下标。

第四个问题：寻找当前元素右侧，离它最近，并且比它小的元素在哪。

从右往左遍历元素，构造一个单调递增的栈。当 while 循环弹栈完成后插入当前位置的元素的时：

• 如果栈为空，则右侧不存在比当前元素小的元素；

• 如果栈非空，插入当前位置元素时的栈顶元素就是所找的元素。

注意，因为我们要找的是最终结果的位置。因此，栈里面存的是每个元素的下标。

通过以上方法，我们可以总结出以下结论：

找左侧，正遍历；找右侧，逆遍历；

比它大，单调减；比它小，单调增。

---

3. 【模板】单调栈 ⭐⭐

【题目链接】

P5788 【模板】单调栈 - 洛谷

【题目背景】

模板题，无背景。

2019.12.12 更新数据，放宽时限，现在不再卡常了。

【题目描述】

给出项数为 $n$ 的整数数列 $a_{1\dots n}$。

定义函数 $f(i)$ 代表数列中第 $i$ 个元素之后第一个大于 $a_i$ 的元素的下标，即 f ( i ) = min ⁡ i < j ≤ n , a j > a i { j } f(i)=\min_{i<j\leq n, a_j > a_i} \{j\} f(i)=mini<j≤n,aj​>ai​​{j}。若不存在，则 $f(i)=0$。

试求出 $f(1\dots n)$。

【输入格式】

第一行一个正整数 $n$。

第二行 $n$ 个正整数 $a_{1\dots n}$。

【输出格式】

一行 $n$ 个整数表示 $f(1),f(2),\dots ,f(n)$ 的值。

【示例一】

输入

5
1 4 2 3 5

输出

2 5 4 5 0

【说明/提示】

数据规模与约定

对于 $30\%$ 的数据，$n\le 100$；

对于 $60\%$ 的数据，$n\le 5\times 10^3$ ；

对于 $100\%$ 的数据，$1\le n\le 3\times 10^6$，$1\le a_i\le 10^9$。

---

很明显，这道题要我们找每一个元素右侧，离它最近，比它大的元素的位置。因此我们只需要逆序遍历数组，并维护一个单调递减的单调栈即可。

#include<iostream>
#include<stack>using namespace std;const int N = 3e6 + 10;
int a[N];
int f[N];  // 存储每一个位置右侧离它最近并且比它大的元素的下标int main()
{int n;cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];stack<int> st;// 逆序遍历数组for(int i = n; i >= 1; i--){// 维护单调递减的单调栈// 如果栈不空并且栈顶元素小于等于 a[i] while(st.size() && a[st.top()] <= a[i]) st.pop();// 此时如果栈不空，则栈顶元素就是要找的位置if(st.size()) f[i] = st.top();// 否则就没有比它大的元素，就存 0else f[i] = 0;st.push(i);}for(int i = 1; i <= n; i++) cout << f[i] << ' ';return 0;
}

---

二、OJ 练习

1. 发射站 ⭐⭐

【题目链接】

P1901 发射站 - 洛谷

【题目描述】

某地有 $N$ 个能量发射站排成一行，每个发射站 $i$ 都有不相同的高度 $H_i$，并能向两边（两端的发射站只能向一边）同时发射能量值为 $V_i$ 的能量，发出的能量只被两边最近的且比它高的发射站接收。显然，每个发射站发来的能量有可能被 $0$ 或 $1$ 或 $2$ 个其他发射站所接受。

请计算出接收最多能量的发射站接收的能量是多少。

【输入格式】

第 $1$ 行一个整数 $N$。

第 $2$ 到 $N+1$ 行，第 $i+1$ 行有两个整数 $H_i$ 和 $V_i$，表示第 $i$ 个发射站的高度和发射的能量值。

【输出格式】

输出仅一行，表示接收最多能量的发射站接收到的能量值。答案不超过 32 位带符号整数的表示范围。

【示例一】

输入

3
4 2 
3 5 
6 10

输出

7

【说明/提示】

对于 $40\%$ 的数据，$1\le N\le 5000,1\le H_i\le 10^5,1\le V_i\le 10^4$。

对于 $70\%$ 的数据，$1\le N\le 10^5,1\le H_i\le 2\times 10^9,1\le V_i\le 10^4$。

对于 $100\%$ 的数据，$1\le N\le 10^6,1\le H_i\le 2\times 10^9,1\le V_i\le 10^4$。

---

(1) 解题思路

很明显的一个用单调栈解决的问题。我们可以用一个数组 val[] 来记录每个发射站接收到的能量总和，对于每一个发射站，我们利用单调栈向左和向右去寻找第一个比它高的发射站，让找到的这两个发射站对应的 val += v[i] 。最后遍历整个 val 数组，找出最大值即可。

---

(2) 代码实现

#include<iostream>
#include<stack>using namespace std;const int N = 1e6 + 10;
int h[N], v[N];  // 分别记录高度和发射的能量大小
int val[N];  // 记录每个发射站接收到的能量总和int main()
{int n; cin >> n;for(int i = 1; i <= n; i++) cin >> h[i] >> v[i];// 向右边发射 -> 向右找大，逆序单减stack<int> st;for(int i = n; i >= 1; i--){while(st.size() && h[st.top()] <= h[i]) st.pop();if(st.size()) val[st.top()] += v[i];st.push(i);}while(st.size()) st.pop();  // 清空栈// 向左边发射 -> 向左找大，正序单减for(int i = 1; i <= n; i++){while(st.size() && h[st.top()] <= h[i]) st.pop();if(st.size()) val[st.top()] += v[i];st.push(i);}int ans = 0;for(int i = 1; i <= n; i++) ans = max(ans, val[i]);cout << ans;return 0;
}

---

2. 最大的矩阵纸片 ⭐⭐⭐

【题目链接】

[B4273 蓝桥杯青少年组省赛 2023] 最大的矩形纸片 - 洛谷

【题目描述】

一张半边参差不齐的网格纸（网格边长均为 $1$），有一边是完整没有破损的。现要从中剪出一片面积最大的矩形纸片。

给定网格纸中完整边的长度 $N$（$1\le N\le 1000000$），以及网格中每一列残存部分的高度（$1\le$ 高度 $\le 10000$），输出能够剪出的最大矩形纸片面积。

【输入格式】

第一行输入一个正整数 $N$（$1\le N\le 1000000$），表示纸片完整边的长度。

第二行输入 $N$ 个正整数（$1\le$ 正整数 $\le 10000$），表示每列格子残存部分的高度，两个正整数之间用一个空格隔开。

【输出格式】

输出一个正整数，表示能够剪出的最大矩形纸片面积。

【示例一】

输入

6
3 2 1 4 5 2

输出

8

---

(1) 解题思路

题意可以理解为给了一排宽度为 1，高度给定的矩形纸片，求能剪出的最大矩形的面积，如图：

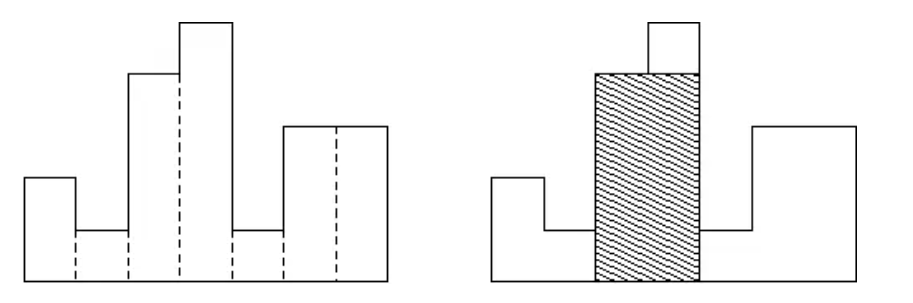
对于一个高度为 h 的矩形，想要从这个位置向左或者向右去拼成一个更大的矩形，很明显，需要它左侧和右侧纸的高度比它高。换言之，我们就是要找它左侧和右侧第一个比它矮的位置，假设左侧第一个比它矮的位置为 l（如果没有，记为 0），右侧第一个比它矮的位置为 r（如果没有，记为 n + 1），那么以当前矩形向两边扩展所能剪出的最大的矩形面积就是 h * (r - l - 1)。

想要求出最大的矩阵面积，只需要对于每一个高度的矩形，都向左和向右寻找第一个比它矮的位置，计算出所能得到的矩形的面积，然后取最大值即可。

---

(2) 代码实现

#include<iostream>
#include<stack>
#include<cmath>using namespace std;typedef long long LL;const int N = 1e6 + 10;
// 分别记录高度，左侧第一个比它小，右侧第一个比它小
LL h[N], l[N], r[N];int main()
{int n; cin >> n;for(int i = 1; i <= n; i++) cin >> h[i];// 向右边找第一个比它小的元素stack<int> st;for(int i = n; i >= 1; i--){while(st.size() && h[st.top()] >= h[i]) st.pop();if(st.size()) r[i] = st.top();else r[i] = n + 1;st.push(i);}while(st.size()) st.pop();// 向左边找第一个比它小的元素for(int i = 1; i <= n; i++){while(st.size() && h[st.top()] >= h[i]) st.pop();if(st.size()) l[i] = st.top();else l[i] = 0;st.push(i);}LL ret = 0;for(int i = 1; i <= n; i++){LL t = h[i] * (r[i] - l[i] - 1);ret = max(ret, t);}cout << ret << endl;return 0;
}