MATLAB基于IOWGA算子的最优组合预测模型及应用
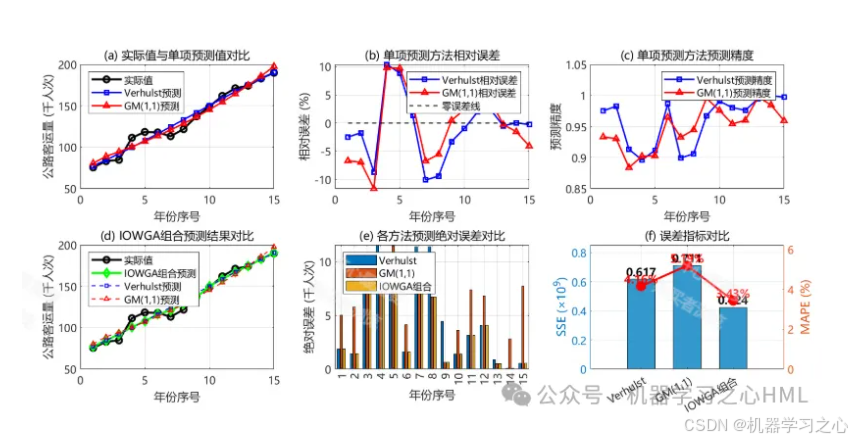
基于IOWGA算子的最优组合预测模型及应用
一、 背景与核心思想
在预测实践中,对于同一个问题,往往存在多种不同的预测模型(如时间序列ARIMA、机器学习SVM/随机森林、深度学习LSTM等)。这些单一模型各有优劣,其预测性能在不同时期可能波动很大。组合预测 的基本思想是“集思广益”,将多个单一模型的预测结果进行综合,以期获得比任何单一模型都更稳定、更精确的最终预测。
IOWGA(Induced Ordered Weighted Geometric Averaging)算子是组合预测中一种先进的信息集成工具。它是对OWA(Ordered Weighted Averaging)算子和OWGA(Ordered Weighted Geometric Averaging)算子的推广。
- 核心创新点:IOWGA算子在集成信息时,不是直接对原始数据排序,而是根据一个“诱导变量”对另一组“主变量”进行重新排序,然后进行加权几何平均。
- 在组合预测中的意义:我们可以将“诱导变量”定义为能够反映各个单一模型在某个时刻预测精度的指标(如预测误差的绝对值或平方),将“主变量”定义为各个模型的预测值。这样,IOWGA算子能够自动地给予在特定时刻预测得更准的模型更大的权重,从而实现动态、自适应的最优组合。
二、 模型构建与原理
假设对于一个预测问题,我们有 ( m ) 种单一的预测方法,在$t $时刻 $ t=1,2,…,n $:
- $f_{it} :第:第:第i $ 种单一模型在 $ t $ 时刻的预测值 $i=1,2,…,m $。
- $x_t $: ttt时刻的实际观测值。
我们的目标是找到一组最优权重w=(w1,w2,...,wm)w = (w_1, w_2, ..., w_m)w=(w1,w2,...,wm),使得组合预测值 $ \hat{x}_t $ 尽可能接近 $x_t $。
1. 定义IOWGA算子
一个IOWGA算子定义为:
IOWGA(⟨u1,a1⟩,⟨u2,a2⟩,...,⟨um,am⟩)=∏j=1mbjwj\text{IOWGA}(\langle u_1, a_1 \rangle, \langle u_2, a_2 \rangle, ..., \langle u_m, a_m \rangle) = \prod_{j=1}^{m} b_j^{w_j} IOWGA(⟨u1,a1⟩,⟨u2,a2⟩,...,⟨um,am⟩)=j=1∏mbjwj
其中:
- $\langle u_i, a_i \rangle $是一个二维数组。
- $u_i $ 称为 诱导变量。
- $ a_i$ 称为 主变量。
- $ w = (w_1, w_2, …, w_m) 是与IOWGA算子相关联的权重向量,满足是与IOWGA算子相关联的权重向量,满足是与IOWGA算子相关联的权重向量,满足 \sum_{j=1}^{m} w_j = 1 $ 且 $ w_j \in [0,1]$。
- bjb_jbj 是主变量 $ a_i $ 中按诱导变量$u_i $从大到小(或从小到大)排序后,排在第 $j $ 位的那个 $a_i $值。
2. 在组合预测中的应用
我们将IOWGA算子引入组合预测模型:
- 主变量 $ a_i $: 第 $ i个模型的预测值个模型的预测值个模型的预测值f_{it}$。
- 诱导变量$u_i $: 反映第 iii个模型在 ttt时刻预测精度的指标。一个常见的选择是预测误差绝对值或平方误差**的倒数。这样,误差越小的模型,其诱导值越大,在排序中会越靠前。
- 组合预测值 $ \hat{x}t ∗∗:在**: 在∗∗:在 t $ 时刻,我们根据诱导变量$ u_i $ 对所有模型的预测值$f{it} $ 进行降序排列。让排序后的预测值序列为b1t,b2t,...,bmtb_{1t}, b_{2t}, ..., b_{mt}b1t,b2t,...,bmt。则组合预测值为:
x^t=∏j=1m(bjt)wj\hat{x}_t = \prod_{j=1}^{m} (b_{jt})^{w_j} x^t=j=1∏m(bjt)wj
这是一个加权几何平均**的形式。
3. 确定最优权重 ( w )
权重的确定是“最优组合预测”的关键。我们通过求解一个优化问题来找到最优权重 $w $,其目标是最小化组合预测的整体误差。
-
目标函数:通常以误差平方和(SSE)或平均绝对百分比误差(MAPE)最小化为目标。
minJ(w)=∑t=1n(x^t−xt)2\min J(w) = \sum_{t=1}^{n} (\hat{x}_t - x_t)^2 minJ(w)=t=1∑n(x^t−xt)2
代入$ \hat{x}t = \prod{j=1}^{m} (b_{jt})^{w_j} $,目标函数变为:
minJ(w)=∑t=1n(∏j=1m(bjt)wj−xt)2\min J(w) = \sum_{t=1}^{n} \left( \prod_{j=1}^{m} (b_{jt})^{w_j} - x_t \right)^2 minJ(w)=t=1∑n(j=1∏m(bjt)wj−xt)2 -
约束条件:
∑j=1mwj=1,wj≥0,j=1,2,...,m\sum_{j=1}^{m} w_j = 1, \quad w_j \ge 0, \quad j=1,2,...,m j=1∑mwj=1,wj≥0,j=1,2,...,m
这是一个典型的非线性规划问题。由于目标函数中包含了幂运算和乘积,通常没有解析解,需要使用数值优化算法进行求解,如序列二次规划法(SQP)、遗传算法(GA) 或 粒子群算法(PSO) 等。
三、 模型优势
与传统的基于线性加权平均(或基于IOWA算子)的组合预测模型相比,基于IOWGA的模型具有显著优势:
- 动态适应性:权重分配不是固定的,而是根据每个时间点上各个模型的精度表现(诱导变量)动态调整。在某个时点表现好的模型会自动获得更高的权重,更加符合现实情况。
- 几何平均的特性:加权几何平均对极端值(特别是极小的预测值)不如算术平均敏感。在处理具有指数增长趋势或比率数据时,几何平均通常比算术平均更具代表性。
- 双重优化:该模型不仅通过优化算法确定了最优的权重向量 ( w ),还通过诱导排序机制在每一个时间点实现了预测值的优化重组。
- 强鲁棒性:由于结合了多个模型的信息,并对精度高的模型赋予更高权重,最终组合模型对异常值和单一模型的失效具有更强的抵抗能力,预测结果更加稳定。
四、 应用步骤
- 数据准备:收集历史数据,并划分训练集和测试集。
- 单一模型预测:使用多种单一的预测模型(如ARIMA, SVM, LSTM等)在训练集上进行建模,并在整个时间序列上得到预测值 fitf_{it}fit。
- 计算诱导变量:对于每个时间点 ttt和每个模型$ i $,计算其诱导值 uitu_{it}uit。
- 排序与重构:在每个时间点 ttt,根据uitu_{it}uit 对$ f_{it}$ 进行降序排列,得到排序后的序列bjtb_{jt}bjt。
- 求解最优权重:构建以误差平方和最小化为目标、以权重和为1为非负为约束的非线性规划模型,并利用优化算法求解出最优权重向量 w∗w^*w∗。
- 进行组合预测:将求解得到的最优权重 $w^* $和排序后的预测值 bjtb_{jt}bjt 代入IOWGA公式,得到最终在各个时间点的组合预测值 x^t\hat{x}_tx^t。
- 模型评估与比较:在测试集上,计算组合预测模型与各个单一预测模型的评价指标(如RMSE, MAE, MAPE),以验证组合模型的有效性。
五、 应用领域
该模型适用于任何存在多种预测方法且需要提高预测精度和稳定性的领域:
- 能源需求预测:电力负荷、天然气消费量预测。
- 经济金融预测:股票价格、汇率、GDP增长率、通货膨胀率预测。
- 销售量预测:零售、电商领域的商品销量预测。
- 交通流量预测:城市道路、高速公路的车流量预测。
- 气象与环境预测:风速、降水量、空气质量指数(AQI)预测。
六、 总结
基于IOWGA算子的最优组合预测模型是一种先进且强大的预测技术。它巧妙地利用了诱导排序机制,将静态的权重分配转化为动态的精度驱动分配,再结合加权几何平均的优良特性,能够有效地综合利用各种单一模型的信息,显著提升预测的准确性和可靠性。尽管其求解过程涉及复杂的非线性优化,但随着计算技术的发展,该模型在各个领域的预测实践中具有极高的应用价值和广阔的前景。
