rnn lstm transformer mamba
深度序列建模发展史的主干脉络:从最早的 RNN(循环神经网络),到 LSTM(长短期记忆网络),再到 Mamba(Selective State Space Model),每一次迭代都解决了前一代的核心缺陷。
| 阶段 | 代表模型 | 时代 | 主要创新 | 目标问题 |
|---|---|---|---|---|
| ① | Vanilla RNN | 1990s | 隐状态递归建模时间序列 | 序列建模、时间依赖 |
| ② | LSTM / GRU | 1997–2014 | 引入门控机制与记忆单元 | 解决梯度消失、长期依赖 |
| ③ | Transformer | 2017 | 自注意力取代递归 | 并行训练、长程建模 |
| ④ | State Space Models (SSM) | 2021–2023 | 连续时间线性状态系统 | 高效长序列建模 |
| ⑤ | Mamba | 2024 | 选择性输入门 + 线性高效并行SSM | 结合RNN记忆力与Transformer吞吐 |
| 模型 | 时间复杂度 | 记忆能力 | 并行性 | 表达能力 |
|---|---|---|---|---|
| RNN | O(L) | 中等 | 低 | 中等 |
| LSTM | O(L) | 强 | 低 | 强 |
| Transformer | O(L²) | 中 | 高 | 强 |
| SSM | O(L log L) | 强 | 高 | 中 |
| Mamba | O(L) | 强 | 高 | 极强 |
1、RNN(Recurrent Neural Network)
ht=tanh(Whhht−1+Wxhxt+b)h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b)ht=tanh(Whhht−1+Wxhxt+b)
yt=Whyht+byy_t = W_{hy}h_t + b_yyt=Whyht+by
明确公式整体作用,两个公式描述了RNN在单个时间步 ttt 的计算逻辑:
- 第一个公式:用「上一时刻隐藏状态」和「当前时刻输入」,更新得到「当前时刻隐藏状态」(核心是“记忆传递”);
- 第二个公式:用「当前时刻隐藏状态」,计算得到「当前时刻输出」(核心是“信息映射”)。
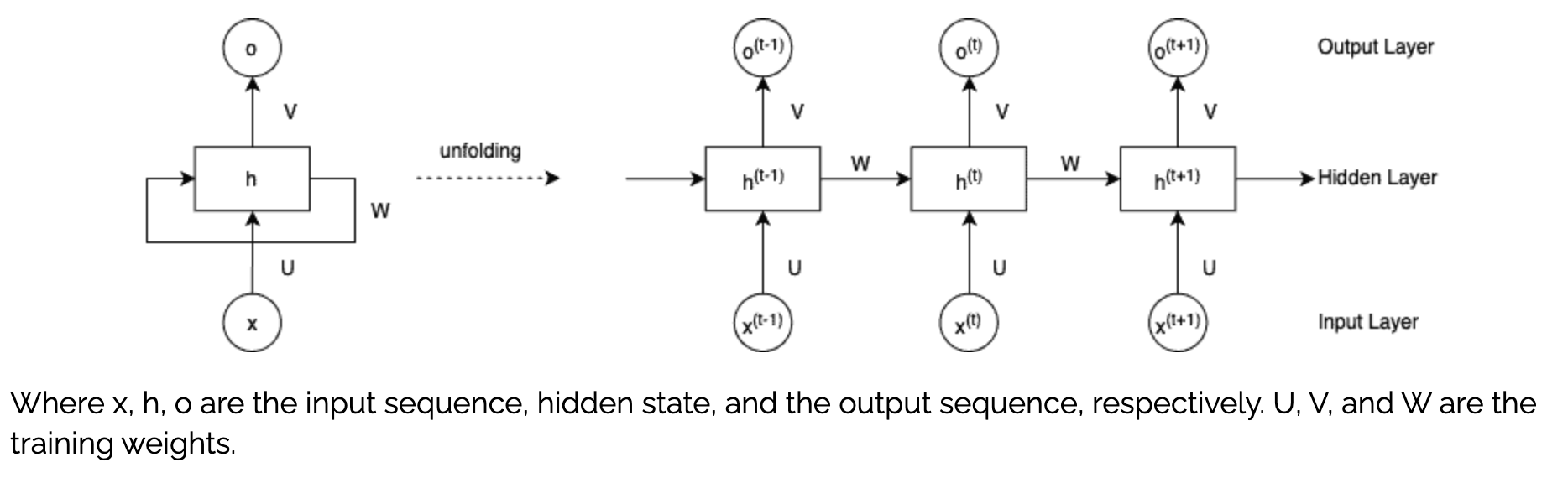
unfolding其实也意味着所有的时刻,UVW权重矩阵是共享的,任意时刻的W矩阵都完全一致。要理解图与公式的对应关系,我们可以从循环神经网络(RNN)的结构元素逐一拆解:
1.1 符号与模块的对应
- 节点 xxx:对应公式中的输入 xtx_txt,表示当前时刻的输入序列元素。
- 模块 hhh:对应公式中的隐藏状态 hth_tht,是RNN的“记忆核心”。它的计算依赖两部分:
- 前一时刻的隐藏状态 ht−1h_{t-1}ht−1(对应图中循环连接 WWW,即公式中的 Whhht−1W_{hh}h_{t-1}Whhht−1);
- 当前时刻的输入 xtx_txt(对应图中连接 UUU,即公式中的 WxhxtW_{xh}x_tWxhxt);
再加上偏置 bbb,通过激活函数 tanh\tanhtanh 得到 ht=tanh(Whhht−1+Wxhxt+b)h_t = \tanh(W_{hh}h_{t-1} + W_{xh}x_t + b)ht=tanh(Whhht−1+Wxhxt+b)。
- 节点 ooo:对应公式中的输出 yty_tyt,由隐藏状态 hth_tht 经权重 WhyW_{hy}Why(对应图中连接 VVV)和偏置 byb_yby 映射得到,即 yt=Whyht+byy_t = W_{hy}h_t + b_yyt=Whyht+by。
1.2 连接的意义
- UUU 连接:输入 xxx 到隐藏层 hhh 的权重传递,对应公式中 WxhW_{xh}Wxh。
- WWW 循环连接:隐藏层 hhh 自身的循环依赖,对应公式中 WhhW_{hh}Whh(体现RNN的“记忆”特性)。
- VVV 连接:隐藏层 hhh 到输出 ooo 的权重传递,对应公式中 WhyW_{hy}Why。
简言之,图中的模块和连接分别对应公式中输入、隐藏状态(含循环依赖)、输出的计算过程,完整体现了RNN“输入→隐藏层(带记忆)→输出”的核心逻辑。
1.3 RNN评估
RNN的输入核心是具有时间先后顺序的序列,且元素间存在依赖关系(如文本中“词”的语义依赖上下文、股票价格依赖历史走势)。输入需被编码为向量序列(每个时间步的输入是一个向量),长度可长可短(从几个时间步到数千个时间步不等)。
例如,处理一句话“我喜欢深度学习”时,输入是5个词的词向量序列(每个词向量维度如200),时间步 ( t=1 ) 对应“我”,( t=2 ) 对应“喜欢”,依此类推,RNN通过循环计算捕捉这些词的语义关联。常用于自然语言处理(文本序列,语音序列);时间序列分析(数值型时序数据,多变量时序数据);计算机视觉(视频帧序列,OCR(字符的像素序列)。诸如此类的有典型顺序关系的数据。
劣势:
1、无法并行计算:每个隐藏状态的计算依赖于上一个隐藏状态的计算结果
2、无法捕捉长期依赖:信息会随着时间步的增加而逐渐稀释,如对于那些在句尾存储着重要信息的语句处理效果差
3、激活函数和权重有乘积效应,会带来梯度消失或者梯度爆炸的问题
2、LSTM(Long Short-Term Memory)
LSTM(Hochreiter & Schmidhuber, 1997)通过引入“门控机制 (Gates)”来控制信息流,解决长期依赖问题。GRU(Gated Recurrent Unit,2014)是 LSTM 的简化版,将一些门合并以减少参数量。
在 RNN(循环神经网络)中,每个时间步的隐藏状态由上一个时间步传递,梯度消失 / 爆炸问题以及长距离记忆消失的问题需要解决,于是1997 年 Sepp Hochreiter & Jürgen Schmidhuber 提出了 LSTM,通过引入“门控机制”解决长期记忆问题。
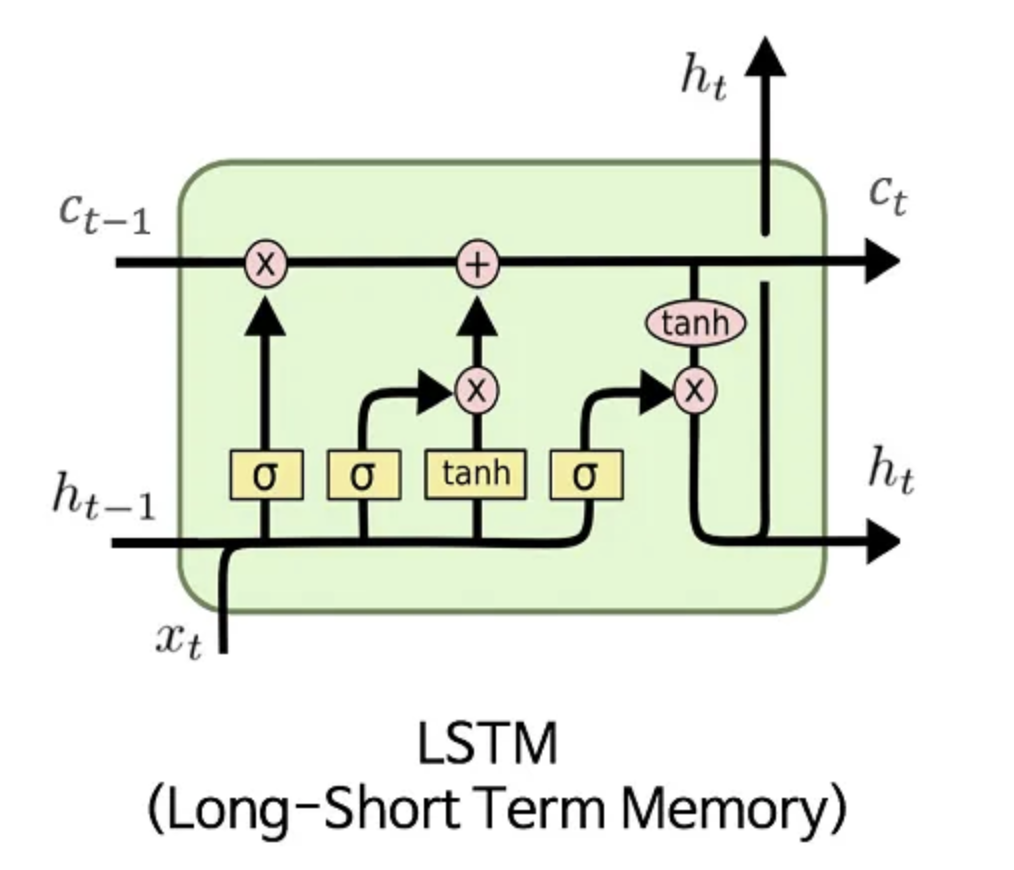
符号说明:
ctc_tct(细胞状态):LSTM 的 “记忆中枢”,是一条贯穿整个结构的信息流,用于长期信息的传递与保存。
hth_tht(隐藏状态):既作为 LSTM 的输出,也参与后续时刻的计算,用于传递短期信息。
σ\sigmaσ(sigmoid 激活函数):输出范围(0,1)(0,1)(0,1),其实也是LSTM算法中的 门控(控制信息的通过比例,0 表示完全阻断,1 表示完全通过)。
tanh\tanhtanh(双曲正切激活函数):输出范围(−1,1)(-1,1)(−1,1),用于生成候选记忆或对细胞状态进行缩放。
×\times×(逐元素乘法)、+++(逐元素加法):用于信息的整合与更新。
LSTM 的工作流程可概括为:
遗忘旧记忆:通过遗忘门ftf_tft筛选上一时刻细胞状态ct−1c_{t-1}ct−1的信息。
存入新记忆:通过输入门iti_tit和候选记忆c~t\tilde{c}_tc~t生成待存入的新信息,与遗忘后的旧记忆结合,更新得到ctc_tct。
输出当前状态:通过输出门oto_tot筛选ctc_tct的信息,生成当前隐藏状态hth_tht,并传递到下一时刻(hth_tht成为ht+1h_{t+1}ht+1的输入,ctc_tct成为ct+1c_{t+1}ct+1的输入)。
2.1 LSTM与梯度消失/爆炸
LSTM并非 “消灭” 了梯度爆炸 / 消失的可能性,而是通过两个核心设计将梯度 “驯服” 在可控范围内:
- 用「细胞状态的逐元素加法」替代「传统 RNN 的隐藏状态矩阵乘法」,让梯度传播摆脱 “指数级连乘” 的陷阱;
- 用「门控信号(0~1 范围)」对每个维度的梯度传递比例做独立控制,实现 “有用梯度顺畅传、无用梯度及时断”,避免无差别链式放大。
以RNN为例:
ht=tanh(Wh⋅[ht−1,xt]+bh)h_t = \tanh(W_h \cdot [h_{t-1}, x_t] + b_h)ht=tanh(Wh⋅[ht−1,xt]+bh)反向传播(BPTT)时,梯度需要沿着时间步回溯,核心是计算「当前损失对历史隐藏状态的梯度」,进而更新权重WhW_hWh。这个梯度的关键项是时间步上的导数连乘:
∂ht∂ht−1=diag(1−tanh2(zt))⋅Wh(zt=Wh⋅[ht−1,xt]+bh)\frac{\partial h_t}{\partial h_{t-1}} = \text{diag}(1 - \tanh^2(z_t)) \cdot W_h \quad (z_t = W_h \cdot [h_{t-1}, x_t] + b_h)∂ht−1∂ht=diag(1−tanh2(zt))⋅Wh(zt=Wh⋅[ht−1,xt]+bh)
其中:
diag(1−tanh2(zt))\text{diag}(1 - \tanh^2(z_t))diag(1−tanh2(zt)) 是tanh\tanhtanh的导数,范围[0,1][0,1][0,1](会让梯度衰减)。
WhW_hWh 是权重矩阵,若其谱范数(可理解为矩阵 “放大能力”)>1>1>1,则连乘后梯度会指数级增长(爆炸);若<1<1<1,则连乘后梯度会指数级衰减(消失)。简单说:传统 RNN 的梯度传播是「矩阵连乘 + 导数衰减」的叠加,本质是 “无控制的链式放大 / 衰减”,时间步越长,梯度越不稳定。
LLSTM 的核心改进是:用 “细胞状态直连路径” 替代传统 RNN 的 “隐藏状态矩阵迭代”,用 “门控” 控制梯度的传递比例,让梯度既能 “顺畅传递”,又不 “无限制放大”。
-
细胞状态的 “直连路径”:LSTM 的细胞状态ctc_tct更新公式是逐元素加法(而非矩阵乘法):ct=ft⊙ct−1+it⊙c~tc_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_tct=ft⊙ct−1+it⊙c~t(⊙\odot⊙表示逐元素乘法)
我们先看反向传播中「当前细胞状态ctc_tct对前一时刻细胞状态ct−1c_{t-1}ct−1的梯度」—— 这是梯度沿时间传递的核心项:
∂ct∂ct−1=diag(ft)\frac{\partial c_t}{\partial c_{t-1}} = \text{diag}(f_t)∂ct−1∂ct=diag(ft)(推导:ctc_tct对ct−1c_{t-1}ct−1的偏导,仅来自第一项ft⊙ct−1f_t \odot c_{t-1}ft⊙ct−1,逐元素求导后就是ftf_tft本身构成的对角矩阵)这个梯度项的关键优势的是:无矩阵连乘:传统 RNN 的梯度项是WhW_hWh的连乘(容易放大 / 衰减),而 LSTM 这里是ftf_tft的逐元素传递(每个维度的梯度独立控制);梯度幅值可控:ftf_tft是 sigmoid 输出,范围[0,1][0,1][0,1],因此∂ct∂ct−1\frac{\partial c_t}{\partial c_{t-1}}∂ct−1∂ct的每个元素都在[0,1][0,1][0,1]之间 —— 不会出现传统 RNN 中 “矩阵连乘导致的指数级缩放”。 -
门控的 “梯度调节”:给梯度装 “开关 + 节流阀”LSTM 的三个门(遗忘门(f_t)、输入门(i_t)、输出门(o_t))不仅控制 “信息的存弃”,更核心的是控制 “梯度的传递”—— 每个门都是梯度传播的 “调节器”。
-
梯度的 “选择性传递”:避免 “无差别链式放大”
传统 RNN 的梯度传播是 “无差别连乘”—— 所有维度的梯度都要经过相同的WhW_hWh矩阵连乘,一旦WhW_hWh范数偏离 1,所有维度的梯度都会同步爆炸 / 消失。
而 LSTM 的梯度传播是 “分维度选择性传递”:每个维度的梯度传递比例由门控信号(ftf_tft、iti_tit、oto_tot)独立控制:比如 “时间信息” 对应的维度ftf_tft≈1,梯度能稳定传递;“无关细节” 对应的维度ftf_tft≈0,梯度被阻断;梯度传递不是 “链式放大”,而是 “分维度比例控制”:即使某个维度的梯度在某一步略有放大,后续门控也能通过降低ftf_tft或iti_tit的取值,将其拉回可控范围。
2.2 LSTM的缺陷
LSTM 是时序依赖型模型,每个时间步的计算都依赖上一时刻的隐藏状态 ht−1h_{t-1}ht−1 和细胞状态 ct−1c_{t-1}ct−1,无法并行处理序列中的多个时间步。每个时间步的更新需经过 “遗忘门筛选旧记忆 → 输入门生成候选记忆 → 细胞状态累加更新 → 输出门筛选隐藏状态”4 步,导致 LSTM 的计算复杂度(时间复杂度 O(T⋅n2)O(T·n^2)O(T⋅n2),TTT 为序列长度,nnn 为隐藏单元数)远高于 GRU。
3. GRU(Gated Recurrent Unit)
GRU(Gated Recurrent Unit,门控循环单元)的核心优势是 “在保持LSTM核心能力的前提下,实现了‘轻量、高效、易落地’” ——它通过简化门控和记忆结构,在不显著损失“捕捉长期依赖、缓解梯度消失”能力的基础上,解决了LSTM参数多、训练慢、调参复杂等痛点,具体优势可分为以下6点,结合实际应用场景说明:
3.1 核心优势:参数更少,训练效率更高(最关键)
GRU将LSTM的3个门(遗忘门、输入门、输出门)简化为2个门(更新门、重置门),同时取消了独立的细胞状态ctc_tct,仅保留1个隐藏状态hth_tht(兼顾长期记忆+短期输出)。
- 参数规模:比LSTM少约1/3(LSTM需学习6个权重矩阵,GRU仅需3个);
- 实际收益:
- 训练速度更快:相同数据量和硬件条件下,GRU的迭代时间比LSTM短20%~40%,适合大规模数据或快速迭代的项目;
- 显存占用更低:参数减少意味着模型占用的GPU/CPU内存更少,可支持更长的序列长度(如文本序列从512步扩展到1024步)或更大的批量大小(batch size),进一步提升训练效率。
场景举例:小公司做文本分类任务(数据量10万条),用GRU训练1小时即可收敛,而LSTM可能需要1.5~2小时,且GRU无需高端GPU就能运行。
3.2 过拟合风险更低,小数据集表现更稳健
模型的过拟合风险与参数复杂度正相关:LSTM参数多、模型容量大,在小数据集(如几万条样本)上容易“死记硬背”噪声信息,导致泛化能力差;而GRU参数少、模型复杂度低,更难拟合噪声,小数据集上的表现更稳定。
场景举例:做方言语音识别(方言数据稀缺,仅1万条音频),GRU能稳定学习语音的时序特征,而LSTM可能因过拟合出现“训练准确率高、测试准确率低”的情况。
3.3 调参更简单,工程落地成本低
GRU的门控逻辑更简洁(2个门替代3个门),需要调节的超参数更少:
- LSTM需关注:隐藏层单元数、学习率、遗忘门偏置(避免初始遗忘过多)、Dropout比例(门控/细胞状态的Dropout需分别设置);
- GRU仅需关注:隐藏层单元数、学习率、Dropout比例(仅需对输入/隐藏状态设置)。
实际收益:减少调参时间,降低工程实现难度——即使是刚接触循环神经网络的开发者,也能快速上手GRU,无需深入纠结门控的精细调优;且GRU的梯度传播路径更简洁,不易出现“梯度异常”,训练过程更稳定(很少出现LSTM偶尔的梯度震荡问题)。
3.4 保持LSTM核心能力:捕捉长期依赖、缓解梯度问题
GRU的简化并非“牺牲性能换效率”,而是在核心能力上与LSTM对齐:
- 缓解梯度消失/爆炸:GRU的隐藏状态hth_tht通过“更新门加权融合”更新(ht=(1−zt)⊙ht−1+zt⊙h~th_t = (1-z_t) \odot h_{t-1} + z_t \odot \tilde{h}_tht=(1−zt)⊙ht−1+zt⊙h~t),梯度传递时被ztz_tzt(0~1范围)控制,不会像传统RNN那样指数级衰减/爆炸;
- 捕捉长期依赖:重置门rtr_trt可筛选历史信息,更新门ztz_tzt可控制新旧记忆比例——当需要保留长距离关键信息时,zt≈0z_t \approx 0zt≈0(保留旧记忆)、rt≈1r_t \approx 1rt≈1(利用历史信息),实现与LSTM类似的长距离记忆传递。
场景验证:在常规序列任务(如短文本生成、时间序列预测、情感分析)中,GRU的准确率与LSTM相差不超过5%,但效率远超LSTM。
总结:GRU的优势核心是“效率与效果的平衡”
GRU的所有优势都围绕一个核心:在不显著损失“捕捉长期依赖、缓解梯度问题”核心能力的前提下,通过结构简化实现“轻量、高效、稳健、易落地” 。
它不是LSTM的“替代品”,而是“优化版”——适合大多数常规序列任务(文本分类、短序列预测、实时推理、小数据集场景);只有在极长序列(如1000+时间步的长文本生成)或对记忆精度要求极高的场景(如复杂机器翻译),LSTM才略占优势,但GRU仍是工程实践中的“首选”,因为它能以更低的成本达到接近LSTM的效果。
4、Transformer
不赘述,在另外一个界面中有详细介绍;另外可以参考:transformer细节原理介绍
而且很明显的一点,transformer和rnn-lstm-gru-ssm-mamba的技术路线根本不是一条,transformer更像是从CNN参考处理思路和方法得到的灵光一现。
5、SSM&Mamba
Mamba 是 2023 年提出的 结构化状态空间模型(Structured State Space Model, SSM) 变体,核心定位是「兼顾 Transformer 的全局依赖捕捉能力 + 线性时间复杂度」,彻底解决了 Transformer 长序列下 O(T2)O(T^2)O(T2) 复杂度的瓶颈。其核心亮点是:未直接使用 Transformer 的自注意力机制,却通过创新设计达到了同等甚至更优的全局依赖捕捉效果,且速度远超 Transformer。
5.1 Mamba 的核心技术原理
Mamba 本质是对传统状态空间模型(SSM)的工程化优化,核心思路是「用线性时间的状态空间更新替代平方时间自注意力,通过结构化设计和动态适配实现全局依赖捕捉」。
5.1.1 基础框架:简化的状态空间模型(SSM)
传统 SSM 通过“状态转移”建模时序依赖,但稠密矩阵运算导致复杂度居高不下。Mamba 对其做了 3 个关键简化,奠定线性复杂度基础:
(1)核心公式(简化版)
- 状态更新:st=At⋅st−1+Bt⋅xts_t = A_t \cdot s_{t-1} + B_t \cdot x_tst=At⋅st−1+Bt⋅xt
其中,st∈RC×Ds_t \in \mathbb{R}^{C \times D}st∈RC×D(CCC 为通道数,DDD 为特征维度)是隐藏状态,xt∈RC×Dx_t \in \mathbb{R}^{C \times D}xt∈RC×D 是当前时间步输入,At、BtA_t、B_tAt、Bt 是输入依赖的动态参数(替代传统 SSM 的固定矩阵)。 - 输出计算:yt=Ct⋅st+D⋅xty_t = C_t \cdot s_t + D \cdot x_tyt=Ct⋅st+D⋅xt
其中,yt∈RC×Dy_t \in \mathbb{R}^{C \times D}yt∈RC×D 是当前时间步输出,CtC_tCt 是动态输出投影参数,DDD 是固定直接映射项(残差连接辅助)。
(2)关键简化设计
- 对角化状态转移矩阵 AtA_tAt:AtA_tAt 设计为对角矩阵(仅对角线有非零值),此时状态更新可拆解为逐维度独立运算:st[c][d]=At[c][d]⋅st−1[c][d]+Bt[c][d]⋅xt[c][d]s_t[c][d] = A_t[c][d] \cdot s_{t-1}[c][d] + B_t[c][d] \cdot x_t[c][d]st[c][d]=At[c][d]⋅st−1[c][d]+Bt[c][d]⋅xt[c][d](ccc 为通道索引,ddd 为特征维度索引)。
优势:彻底避免矩阵连乘,单步状态更新复杂度从 O(n2)O(n^2)O(n2) 降至 O(n)O(n)O(n)(n=C×Dn=C \times Dn=C×D)。 - 输入/输出投影的结构化:Bt、CtB_t、C_tBt、Ct 均设计为与输入维度对齐的向量(而非稠密矩阵),通过 1×1 卷积动态生成,进一步降低计算量。
5.1.2 核心创新:选择性扫描(Selective Scan)—— 替代自注意力的“动态依赖捕捉”
Mamba 未使用 Transformer 的自注意力机制,但通过「选择性扫描」实现了类似的“全局依赖精准捕捉”,这是其核心技术突破:
(1)解决的问题
传统 SSM 的 A、B、CA、B、CA、B、C 是固定参数,无法根据输入内容动态调整权重——对长序列中的“关键信息”和“冗余信息”一视同仁,依赖捕捉精度不足。
(2)核心设计:输入依赖的动态参数
Mamba 让 At、Bt、CtA_t、B_t、C_tAt、Bt、Ct 成为当前输入 xtx_txt 的函数,通过 1×1 卷积和激活函数(如 Swish)动态生成:
- At=σ(WA⋅LayerNorm(xt)+bA)A_t = \sigma(W_A \cdot \text{LayerNorm}(x_t) + b_A)At=σ(WA⋅LayerNorm(xt)+bA)(σ\sigmaσ 为 Sigmoid 激活,限制 At∈[0,1]A_t \in [0,1]At∈[0,1])
- Bt=WB⋅LayerNorm(xt)+bBB_t = W_B \cdot \text{LayerNorm}(x_t) + b_BBt=WB⋅LayerNorm(xt)+bB
- Ct=WC⋅LayerNorm(xt)+bCC_t = W_C \cdot \text{LayerNorm}(x_t) + b_CCt=WC⋅LayerNorm(xt)+bC
(3)动态依赖捕捉逻辑
- 当输入 xtx_txt 是「长距离关键信息」(如长文本的主题词):BtB_tBt 取值增大(强化该信息对状态 sts_tst 的影响),AtA_tAt 取值接近 1(让状态中存储的历史关键信息不被遗忘);
- 当输入 xtx_txt 是「冗余信息」(如文本中的填充词):BtB_tBt 取值减小(弱化对状态的干扰),AtA_tAt 取值接近 0(快速遗忘该信息对应的历史状态)。
这种设计本质是「动态筛选全局依赖」,效果等价于 Transformer 自注意力的“聚焦关键位置”,但计算量从 O(T2)O(T^2)O(T2) 降至 O(T)O(T)O(T)。
5.1.3 工程优化:硬件感知并行(Hardware-Aware Parallelism)—— 速度快的关键工程保障
Mamba 虽存在“状态更新逐时间步依赖(sts_tst 依赖 st−1s_{t-1}st−1)”,但通过维度拆分和硬件适配,实现了高效并行:
(1)多批次+多通道批量并行
不同批次(BBB)、不同通道(CCC)的状态更新完全独立(样本 1 的通道 1 状态与样本 2 的通道 2 状态无关)。GPU 张量核心可同时处理 B×CB \times CB×C 个独立的状态更新任务(如 64 个样本 × 128 个通道 = 8192 个并行任务),将“逐时间步串行”限制在单个“样本-通道对”内部,整体并行效率拉满。
Mamba 没有 “放弃通道间交流”,而是把 “交流” 和 “并行” 做了 “时间拆分”——先通过高效的投影 + 门控解决 “通道重要性区分”,再通过独立并行解决 “时序更新效率”,既避开了 Transformer 自注意力的 O(T²) 复杂度,又解决了传统 SSM 通道无交互的。对比GRU/LSTM,则是 “通道间交互和时序更新交织在一起”(比如隐藏状态的更新同时涉及通道融合和时序依赖),效率较低;而 Mamba 把这两件事拆开,分别用最优方式处理,所以并行效率更高短板,这也是它能兼顾 “快” 和 “准” 的核心原因。
(2)分块流水线并行
对长序列(如 T=10000T=10000T=10000),将其拆分为多个小块(如 T=10000T=10000T=10000 拆为 10 个 L=1000L=1000L=1000 的小块):
- 小块内部:逐时间步执行状态更新(s1→s2→...→sLs_1 \to s_2 \to ... \to s_Ls1→s2→...→sL);
- 小块之间:通过流水线并行重叠执行(第 1 个小块执行到第 500 步时,第 2 个小块开始初始化),且前一个小块的最终状态 sLs_LsL 作为后一个小块的初始状态 s0s_0s0,保证记忆连续性;
- 优势:既避免长序列单步显存爆炸,又将时间步串行的耗时压缩到小块内部,整体耗时线性增长。
(3)指令级优化
状态更新的核心是“逐元素乘加”(st[c][d]=At[c][d]⋅st−1[c][d]+Bt[c][d]⋅xt[c][d]s_t[c][d] = A_t[c][d] \cdot s_{t-1}[c][d] + B_t[c][d] \cdot x_t[c][d]st[c][d]=At[c][d]⋅st−1[c][d]+Bt[c][d]⋅xt[c][d]),适配 GPU 专用指令(如 CUDA 的 warp-level primitives、Tensor Core 的 wmma),单个操作延迟低至纳秒级,进一步压缩串行耗时。
5.2 Mamba 的时间复杂度
5.2.1 核心复杂度公式
- 时间复杂度:O(T⋅n)O(T \cdot n)O(T⋅n)(TTT 为序列长度,n=C×Dn=C \times Dn=C×D 为隐藏层总维度)
- 空间复杂度:O(T⋅n)O(T \cdot n)O(T⋅n)(仅存储输入、输出和中间状态,无 T2T^2T2 规模的注意力矩阵)
5.2.2 与 Transformer/LSTM 的复杂度对比
| 模型 | 时间复杂度 | 核心依赖项 | 长序列(T=10000T=10000T=10000,n=512n=512n=512)计算量量级 |
|---|---|---|---|
| Mamba | O(T⋅n)O(T \cdot n)O(T⋅n) | TTT(线性)、nnn(线性) | 5.12×1065.12 \times 10^65.12×106(无爆炸风险) |
| Transformer | O(T2⋅n)O(T^2 \cdot n)O(T2⋅n) | TTT(平方)、nnn(线性) | 5.12×10115.12 \times 10^{11}5.12×1011(计算量爆炸) |
| LSTM/GRU | O(T⋅n2)O(T \cdot n^2)O(T⋅n2) | TTT(线性)、nnn(平方) | 2.68×1092.68 \times 10^92.68×109(nnn 增大时爆炸) |
5.2.3 复杂度优势关键
- 无平方项:TTT 和 nnn 均为线性依赖,TTT 翻倍时计算量仅翻倍,彻底摆脱 Transformer 的 T2T^2T2 瓶颈;
- 轻量计算:动态参数生成依赖 1×1 卷积(O(T⋅n)O(T \cdot n)O(T⋅n)),状态更新依赖逐元素操作(O(T⋅n)O(T \cdot n)O(T⋅n)),无高复杂度矩阵乘法。
5.3 Mamba 为什么比 Transformer 快?
Mamba 对 Transformer 的速度优势,源于「复杂度阶数碾压」和「并行效率优化」的双重作用,核心原因有 3 点:
5.3.1 复杂度阶数本质差异(最核心)
Transformer 的核心是自注意力机制,需计算“所有位置对之间的相似度”,产生 T2T^2T2 个位置对的计算量和存储量:
- 自注意力公式:Attention(Q,K,V)=softmax(QKTdk)V\text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})VAttention(Q,K,V)=softmax(dkQKT)V,其中 Q,K,V∈RT×dkQ,K,V \in \mathbb{R}^{T \times d_k}Q,K,V∈RT×dk,QKTQK^TQKT 的计算复杂度为 O(T2⋅dk)O(T^2 \cdot d_k)O(T2⋅dk),存储复杂度也为 O(T2⋅dk)O(T^2 \cdot d_k)O(T2⋅dk);
- 长序列下(如 T=10000T=10000T=10000),T2T^2T2 带来的计算量和显存占用呈指数级爆炸,即使有 FlashAttention 等优化,也只能缓解显存压力,无法改变 T2T^2T2 的复杂度本质。
而 Mamba 的复杂度是 O(T⋅n)O(T \cdot n)O(T⋅n),长序列下计算量线性增长,且无需存储 T2T^2T2 规模的注意力矩阵,显存和速度双重无压力。
5.3.2 并行效率更适配 GPU 硬件
- Transformer 的并行性局限:虽然能并行处理所有时间步的输入,但自注意力的 QKTQK^TQKT 矩阵乘法存在内部依赖,且 T2T^2T2 计算量导致 GPU 算力无法充分释放(长序列下多是“计算密集”而非“并行密集”);
- Mamba 的并行性优势:将“必须串行的时间步依赖”压缩到极小范围(单个样本-通道对的逐元素操作),同时让“批次、通道、特征”等可并行维度充分利用 GPU 张量核心,算力利用率可达 70%~90%(Transformer 约 50%~70%)。
5.3.3 无冗余计算和存储开销
- Transformer 需额外计算位置编码、多头注意力的拼接与投影,且注意力矩阵的 softmax 操作存在数值稳定性开销;
- Mamba 的计算流程极简:输入 → 动态生成参数 → 选择性扫描(状态更新+输出)→ 前馈网络,无冗余步骤,且逐元素操作和 1×1 卷积均为 GPU 高效计算模式。
5.4 Mamba 与注意力机制的关系:替代而非结合
关键结论:Mamba 没有结合 Transformer 的自注意力机制,而是通过「选择性扫描」实现了对自注意力的“功能替代”—— 两者目标一致(捕捉全局依赖),但实现路径和复杂度完全不同:
| 对比维度 | Transformer 自注意力 | Mamba 选择性扫描 |
|---|---|---|
| 核心机制 | 计算所有位置对的相似度,加权聚合信息 | 动态调整状态转移参数,筛选关键历史信息 |
| 复杂度 | O(T2⋅n)O(T^2 \cdot n)O(T2⋅n)(平方) | O(T⋅n)O(T \cdot n)O(T⋅n)(线性) |
| 依赖捕捉范围 | 全局依赖(直接建模任意位置关联) | 全局依赖(通过状态传递间接建模) |
| 动态适配能力 | 依赖相似度权重动态调整 | 依赖输入内容动态调整状态转移参数 |
| 硬件适配性 | 长序列下并行效率受限 | 全维度并行,GPU 算力利用率高 |
简单说:Mamba 用更高效的方式实现了自注意力的核心功能,且彻底摆脱了自注意力的复杂度瓶颈。
5.5 mamba和transformer技术总结
Mamba 的核心技术原理可概括为:用“对角化 SSM 简化计算”+“选择性扫描动态捕捉依赖”+“硬件感知并行优化提速”,最终实现“线性复杂度下的全局依赖捕捉”。
其比 Transformer 快的本质是「复杂度阶数的胜利」+「并行效率的优化」:O(T⋅n)O(T \cdot n)O(T⋅n) 线性复杂度解决了长序列计算爆炸问题,硬件适配的并行设计让线性复杂度充分转化为实际速度优势。在长序列场景(T≥2048T \geq 2048T≥2048),Mamba 比 Transformer 快 10~100 倍;在中短序列场景,速度接近或略快,且效果持平,成为 Transformer 之后序列模型的重要突破。
