当前位置：首页 > news >正文

PyTorch深度学习进阶（二）（批量归一化）

news 2025/11/9 7:02:18

批量归一化

在每个批量里，1个像素是1个样本。与像素（样本）对应的通道维，就是特征维。

所以不是对单个通道的特征图做均值方差，是对单个像素的不同通道做均值方差。

输入9个像素(3x3), 输出3通道，以通道作为列分量，每个像素都对应3列(输出通道=3)，可以列出表格，按列求均值和方差，其实和全连接层一样的。即像素为样本，通道为特征。

这个小批量数据实随机的，算出来的统计量也可以说是随机的。

因为每个batch的均值和方差都不太一样。

因为每次取得batch中的数据都是不同的，所以在batch中计算的均值和方差也是不同的，所以引入了随机性。

总结

当每一个层的均值和方差都固定后，学习率太大的话，靠近loss上面的梯度太大，就梯度爆炸了，学习率太小的话，靠近数据的梯度太小了，就算不动（梯度消失）。
将每一层的输入放在一个差不多的分布里，就可以用一个比较大的精度了，就可以加速收敛速度。
归一化不会影响数据分布，它一点都不会影响精度，变好变坏都不会。

批量归一化代码

使用自定义

Batch Normalization函数

X为输入，gamma、beta为学习的参数。moving_mean、moving_var为全局的均值、方差。eps为避免除0的参数。momentum为更新moving_mean、moving_var的动量。

def batch_norm(X,gamma,beta,moving_mean,moving_var,eps,momentum):

'is_grad_enabled' 来判断当前模式是训练模式还是预测模式。

在做推理的时候，推理不需要反向传播，所以不需要计算梯度

if not torch.is_grad_enabled():

做推理时，可能只有一个图片进来，没有一个批量进来，因此这里用的全局的均值、方差。

在预测中，一般用整个预测数据集的均值和方差。加eps为了避免方差为0，除以0了

X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)

公式：

$\hat{X} = \frac{X - \mu_{\text{moving}}}{\sqrt{\sigma^2_{\text{moving}} + \varepsilon}}$

训练模式

限制输入维度2和4，批量数+通道数+图片高+图片宽=4

else:assert len(X.shape) in (2, 4)

2表示有两个维度，样本和特征，代表全连接层 (batch_size, feature)

求均值，即对每一列求一个均值出来。mean为1*n的行向量
求方差，即对每一列求一个方差出来。ver也为1*n的行向量

if len(X.shape) == 2:mean = X.mean(dim=0)var = ((X - mean) ** 2).mean(dim=0)

4个维度代表卷积层（batch_size, channels, height, width）

mean求均值，0为批量大小，1为输出通道，2、3为高宽。这里是沿着通道维度求均值，0为batch内不同样本，2、3 为同一通道层的所有值求均值，获得一个1*n*1*1的4D向量。
var求方差，同样对批量维度、高宽取方差。每个通道的每个像素位置计算均值方差。

else:mean = X.mean(dim=(0, 2, 3), keepdim=True)var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)

标准化

X_hat = (X - mean) / torch.sqrt(var + eps)

累加，将计算的均值累积到全局的均值上，更新moving_mean

moving_mean = momentum * moving_mean + (1.0 - momentum) * mean

当前全局的方差与当前算的方差做加权平均，最后会无限逼近真实的方差。仅训练时更新，推理时不更新。

moving_var = momentum * moving_var + (1.0 - momentum) * var

Y 为归一化后的输出

Y = gamma * X_hat + beta 
return Y, moving_mean.data, moving_var.data

创建一个正确的BatchNorm图层

Batch Normalization 层类定义和初始化

class BatchNorm(nn.Module):def __init__(self, num_features, num_dims):super().__init__()

num_features 为 feature map 的数量，即通道数的多少

if num_dims == 2:shape = (1, num_features)
else:shape = (1, num_features, 1, 1)

创建可学习的缩放参数与偏移参数，伽马初始化为全1，贝塔初始化为全0，伽马为要拟合的均值，贝塔为要拟合的方差

self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))

创建移动平均统计量，伽马、贝塔需要在反向传播时更新，所以放在nn.Parameter里面，moving_mean、moving_var不需要迭代，所以不放在里面

self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)

向前传播函数

设备同步，因为不是nn.Parameter不会自动移动到GPU

def forward(self, X):if self.moving_mean.device != X.device:self.moving_mean = self.moving_mean.to(X.device)self.moving_var = self.moving_var.to(X.device)

调用 batch_norm 函数

Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean, self.moving_var, eps=1e-5, momentum=0.9)
return Y

应用BatchNorm于LeNet模型

每个卷积层和线性层后面加了BatchNorm

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5),BatchNorm(6, num_dims=4),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5),BatchNorm(16, num_dims=4),nn.Sigmoid(),nn.MaxPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(16*4*4, 120),BatchNorm(120, num_dims=2),nn.Sigmoid(),nn.Linear(120, 84), BatchNorm(84, num_dims=2),nn.Sigmoid(),nn.Linear(84, 10)
)

层序号	层类型	输入形状	输出形状	参数
1	Conv2d	[B, 1, 28, 28]	[B, 6, 24, 24]	1→6, k=5
2	BatchNorm	[B, 6, 24, 24]	[B, 6, 24, 24]	6 通道
3	Sigmoid	[B, 6, 24, 24]	[B, 6, 24, 24]	-
4	MaxPool2d	[B, 6, 24, 24]	[B, 6, 12, 12]	2×2
5	Conv2d	[B, 6, 12, 12]	[B, 16, 8, 8]	6→16, k=5
6	BatchNorm	[B, 16, 8, 8]	[B, 16, 8, 8]	16 通道
7	Sigmoid	[B, 16, 8, 8]	[B, 16, 8, 8]	-
8	MaxPool2d	[B, 16, 8, 8]	[B, 16, 4, 4]	2×2
9	Flatten	[B, 16, 4, 4]	[B, 256]	-
10	Linear	[B, 256]	[B, 120]	256→120
11	BatchNorm	[B, 120]	[B, 120]	120 特征
12	Sigmoid	[B, 120]	[B, 120]	-
13	Linear	[B, 120]	[B, 84]	120→84
14	BatchNorm	[B, 84]	[B, 84]	84 特征
15	Sigmoid	[B, 84]	[B, 84]	-
16	Linear	[B, 84]	[B, 10]	84→10

在Fashion-MNIST数据集上训练网络

设置超参数

lr,num_epochs,batch_size = 1.0, 10, 256

加载数据

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

开始训练，训练函数为上节设置过的train_ch6，详情查看PyTorch深度学习进阶（一）

train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

结果：

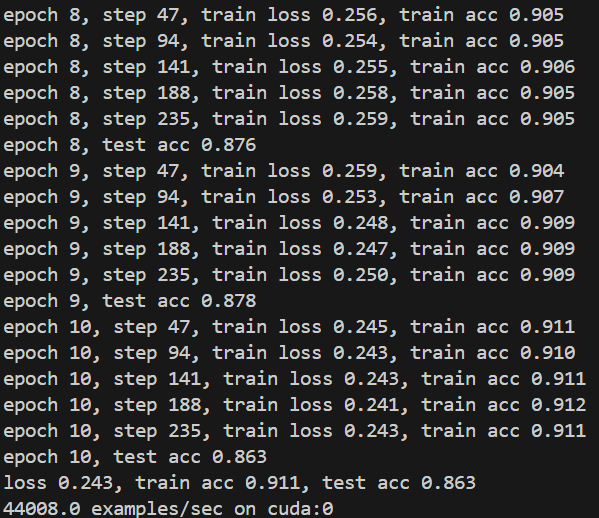
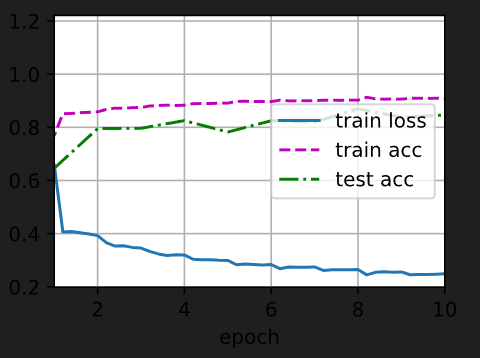
在Jupyter 环境中可视化表示：

ide里终端输出：

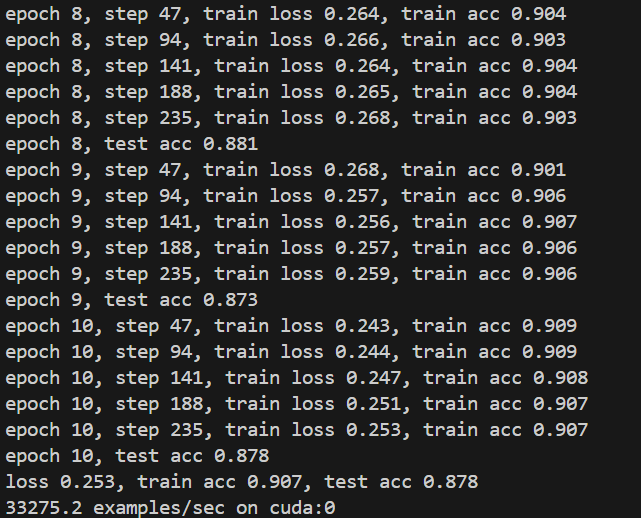
可以明显看出优于上一节不加批量归一化的结果

完整代码

import matplotlib
matplotlib.use('Agg')import torch
from torch import nn
from d2l import torch as d2ldef batch_norm(X, gamma, beta, moving_mean, moving_var, eps=1e-5, momentum=0.9):if not torch.is_grad_enabled():X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)else:assert len(X.shape) in (2, 4)if len(X.shape) == 2:mean = X.mean(dim=0)var = ((X - mean) ** 2).mean(dim=0)else:mean = X.mean(dim=(0, 2, 3), keepdim=True)var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)X_hat = (X - mean) / torch.sqrt(var + eps)moving_mean = momentum * moving_mean + (1 - momentum) * meanmoving_var = momentum * moving_var + (1 - momentum) * varY = gamma * X_hat + betareturn Y, moving_mean.data, moving_var.dataclass BatchNorm(nn.Module):def __init__(self, num_features, num_dims):super().__init__()if num_dims == 2:shape = (1, num_features)else:shape = (1, num_features, 1, 1)self.gamma = nn.Parameter(torch.ones(shape))self.beta = nn.Parameter(torch.zeros(shape))self.moving_mean = torch.zeros(shape)self.moving_var = torch.ones(shape)def forward(self, X):if self.moving_mean.device != X.device:self.moving_mean = self.moving_mean.to(X.device)self.moving_var = self.moving_var.to(X.device)Y, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean, self.moving_var, eps=1e-5, momentum=0.9)return Ydef evaluate_accuracy_gpu(net, data_iter, device=None): if isinstance(net, torch.nn.Module):net.eval()if not device:device = next(iter(net.parameters())).devicemetric = d2l.Accumulator(2)for X, y in data_iter:if isinstance(X, list):X = [x.to(device) for x in X]else:X = X.to(device)y = y.to(device)metric.add(d2l.accuracy(net(X), y), y.numel())return metric[0] / metric[1]def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):"""Train a model with CPU or GPU."""def init_weights(m):if type(m) == nn.Linear or type(m) == nn.Conv2d:nn.init.xavier_uniform_(m.weight)net.apply(init_weights)print('training on', device)net.to(device)optimizer = torch.optim.SGD(net.parameters(), lr=lr)loss = nn.CrossEntropyLoss()timer, num_batches = d2l.Timer(), len(train_iter)for epoch in range(num_epochs):metric = d2l.Accumulator(3)net.train()for i, (X, y) in enumerate(train_iter):timer.start()optimizer.zero_grad()X, y = X.to(device), y.to(device)y_hat = net(X)l = loss(y_hat, y)l.backward()optimizer.step()with torch.no_grad():metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])timer.stop()train_l = metric[0] / metric[2]train_acc = metric[1] / metric[2]if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:print(f'epoch {epoch + 1}, step {i + 1}, train loss {train_l:.3f}, train acc {train_acc:.3f}')test_acc = evaluate_accuracy_gpu(net, test_iter)print(f'epoch {epoch + 1}, test acc {test_acc:.3f}')print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, test acc {test_acc:.3f}')print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec on {str(device)}')net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Flatten(),nn.Linear(16*4*4, 120),BatchNorm(120, num_dims=2), nn.Sigmoid(),nn.Linear(120, 84), BatchNorm(84, num_dims=2),nn.Sigmoid(), nn.Linear(84, 10)
)if __name__ == '__main__':lr, num_epochs, batch_size = 1.0, 10, 256train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

使用现成的框架

直接使用提供的BatchNorm2d，其他操作和训练超参数不变

net = nn.Sequential(nn.Conv2d(1,6,kernel_size=5),nn.BatchNorm2d(6),nn.Sigmoid(),nn.MaxPool2d(kernel_size=2,stride=2),nn.Conv2d(6,16,kernel_size=5),nn.BatchNorm2d(16),nn.Sigmoid(),nn.MaxPool2d(kernel_size=2,stride=2),nn.Flatten(),nn.Linear(256,120),nn.BatchNorm1d(120),nn.Sigmoid(),nn.Linear(120,84),nn.BatchNorm1d(84),nn.Sigmoid(),nn.Linear(84,10)
)

结果