【数据结构】从零开始认识图论 --- 并查集与最小生成树算法

挫折会来也会过去，

热泪会流下也会收起，

没有什么可以让我气馁的，

因为，我有着长长的一生。

--- 席慕蓉 《写给幸福》---

---

1 图的基本概念

在现实世界中，对于地图，网络连接等等场景，之前的数组，栈，队列…都不能很好表示，于是图就是解决这种问题的。

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：顶点集合V = {x | x属于某个数据对象集} 是有穷非空集合；

E = {(x,y) |x , y 属于 V } 或者 **E = {<x, y> | x , y 属于V && Path( x , y) }**是顶点间关系的有穷集合，也叫做边的集合

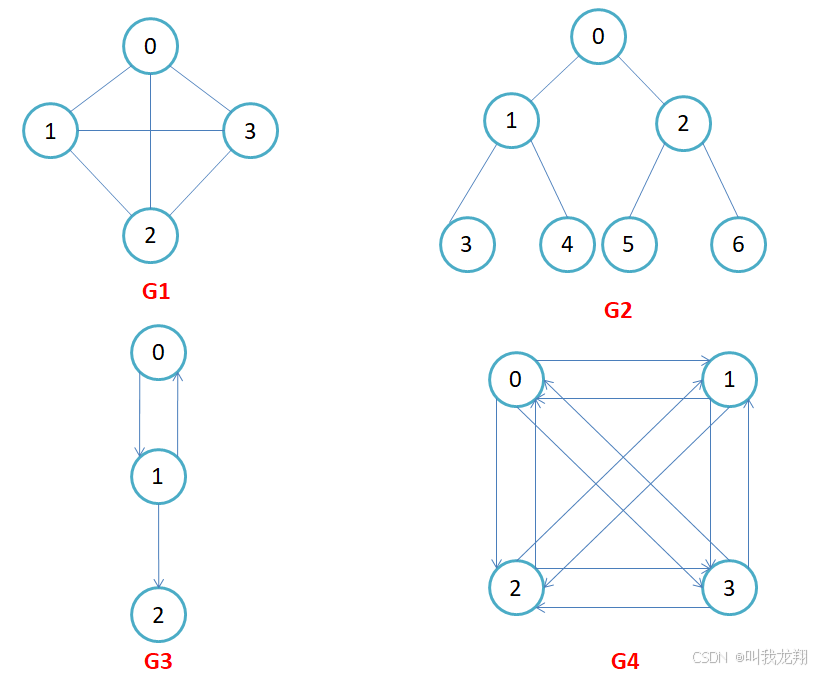
直白一点：图就是由一系列的顶点和边组成的。图中结点称为顶点，第 i 个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。

图有几个概念：有向图和无向图：

1. 在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y, x>是两条不同的边，比如图G3和G4为有向图。
2. 在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边，比如图G1和G2为无向图。注意：无向边(x, y)等于有向边<x, y>和<y, x>

完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G1；在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如上图G4。完全图是最稠密的图

邻接顶点：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联。

顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v)；顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：对于无向图，顶点的度等于该顶点的入度和出度，即 dev(v) = indev(v) = outdev(v)。

路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。

路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和。

2 图的储存结构

2.1 邻接矩阵

储存图的关键是储存节点信息以及边的关系。最直接的就是使用一个邻接矩阵和一个数组。

因为节点与节点之间的关系就是连通与否，即为0或者1，可以继续赋予对应的权值。接着储存节点与下标的映射关系，因此邻接矩阵(二维数组)即是：先用一个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。

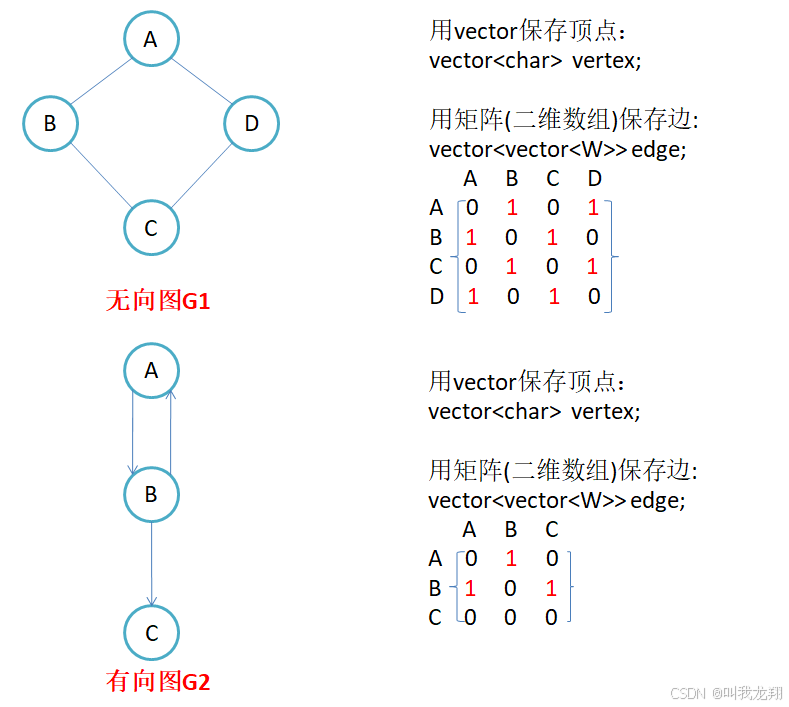
注意：

1. 无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一定是对称的，第i行(列)元素之后就是顶点i 的出(入)度。
2. 如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个顶点不通，则使用无穷大（最大权值）代替。
   
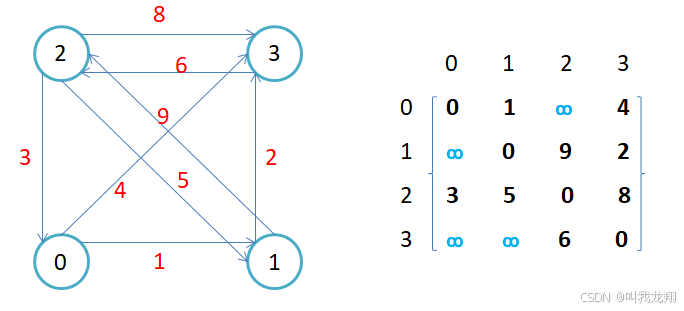
3. 用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求。

优点

• 判断两顶点是否相邻效率极高
• 存储结构简单，实现直观基于二维数组，逻辑清晰，容易理解和实现。初始化、访问、修改边的操作都可通过数组索引直接完成，无需复杂的指针或链表操作。
• 便于计算图的相关特性可通过矩阵运算（如矩阵乘法）快速求解图的路径问题（如两点间的最短路径条数、可达性等），适合理论分析和算法推导。

缺点

• 空间复杂度高，不适合稀疏图无论图中实际有多少条边，邻接矩阵都需要 n×n 的存储空间，空间复杂度为 O(n²)。对于稀疏图（边数 e << n²，如社交网络、道路网），会造成大量存储空间的浪费（大部分元素为 0 或 ∞）。
• 遍历顶点的邻接点效率低若要获取顶点 i 的所有邻接点，需要遍历整个第 i 行（共 n 个元素），时间复杂度为 O(n)，即使该顶点只有少数几个邻接点。
• 动态增删顶点成本高若要新增或删除顶点，需要重新创建一个 (n±1)×(n±1) 的矩阵并复制原有数据，时间复杂度为 O(n²)，操作成本高。

适用场景

1. 稠密图（如完全图），空间浪费少。
2. 需要频繁判断两顶点是否相邻的场景（如最短路径算法中的松弛操作）。
3. 对存储空间不敏感，但对查询效率要求高的场景。
4. 理论研究或需要矩阵运算辅助的算法（如 Floyd-Warshall 最短路径算法）。

2.2 邻接表

临
界表直接储存的是边的集合

1. 顶点用数组存储：每个数组元素代表一个顶点，存储顶点的基本信息（如编号、值等）。
2. 边用链表存储：每个顶点对应的链表，记录与该顶点直接相邻的所有顶点（即边的另一端顶点），以及边的相关信息（如权重，适用于带权图）。
   
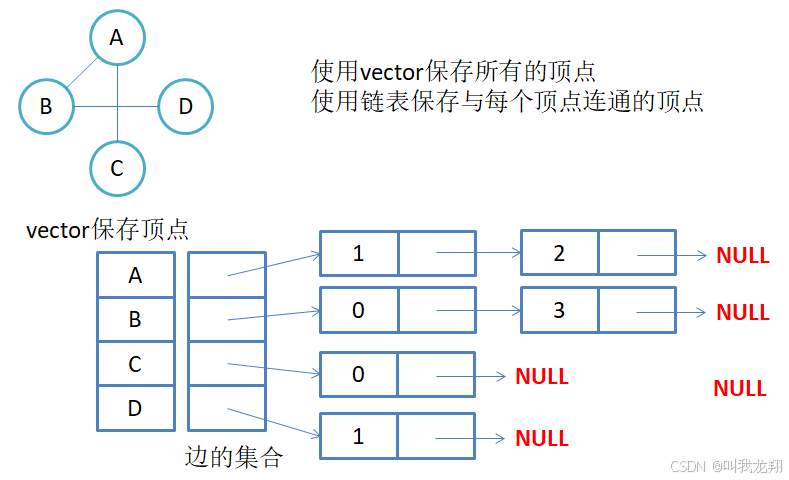
   优点：

• 空间效率高：仅存储实际存在的边，稀疏图中空间复杂度为 O(n + e)（n 为顶点数，e 为边数），远优于邻接矩阵的 O(n²)。
• 便于遍历：遍历一个顶点的所有邻接点（如深度优先搜索、广度优先搜索）时，只需遍历其对应的链表，时间复杂度为 O(k)（k 为邻接顶点数）。
• 动态性好：新增 / 删除边时，只需操作对应链表的节点，无需像邻接矩阵那样修改整个数组。

缺点：

• 判断两顶点是否相邻效率低：需遍历其中一个顶点的链表，时间复杂度为 O(k)，而邻接矩阵可直接通过索引访问（O(1)）。
• 无向图中每条边需存储两次（双向），略有冗余。

邻接表适用于：

1. 稀疏图中如社交网络（每个人的好友数远小于总人数）。
2. 需频繁遍历顶点邻接点的场景（如图的搜索、最短路径算法）。
3. 动态增删边的场景。

2.3 图的邻接矩阵实现

//		顶点数据类型	权值类型	  默认不联通距离		是否有向图
template<class T , class W , W MAX_W = INT_MAX , bool direction = false>
class Graph {
public:typedef Graph<T, W, MAX_W, direction> Self;Graph() = default;//构造函数Graph(const vector<T>& v) {_size = v.size();_vertexs.resize(_size, T());for (int i = 0; i < _size; i++) {_vertexs[i] = v[i];//储存顶点与下标的关系_vIndexs[v[i]] = i;_indexVs[i] = v[i];}//初始化边关系_map.resize(_size, vector<W>(_size, MAX_W));}//获取下标size_t getVertexIndex(const T& v){auto ret = _vIndexs.find(v);if (ret != _vIndexs.end()){return ret->second;}else{throw invalid_argument("不存在的顶点");return -1;}}//添加边void _addEdge(const size_t src, const size_t dst, const W& weight) {_map[src][dst] = weight;if (direction == false) {_map[dst][src] = weight;}return;}void addEdge(const T& src , const T& dst , const W& weight) {size_t index1 = getVertexIndex(src);size_t index2 = getVertexIndex(dst);_addEdge(index1, index2, weight);}//打印void Print(){// 顶点for (size_t i = 0; i < _vertexs.size(); ++i){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;// 矩阵// 横下标cout << "  ";for (size_t i = 0; i < _vertexs.size(); ++i){//cout << i << " ";printf("%4d", i);}cout << endl;for (size_t i = 0; i < _size; ++i){cout << i << " "; // 竖下标for (size_t j = 0; j < _size; ++j){//cout << _matrix[i][j] << " ";if (_map[i][j] == MAX_W){//cout << "* ";printf("%4c", '*');}else{//cout << _matrix[i][j] << " ";printf("%4d", _map[i][j]);}}cout << endl;}cout << endl;}private:vector<T> _vertexs;//储存顶点的数组unordered_map<T, size_t> _vIndexs;//储存顶点与下标的映射关系unordered_map<T, size_t> _indexVs;//储存下标与顶点的映射关系vector<vector<W>> _map;//储存顶点路径关系 size_t _size = 0;
};

3 最小生成树算法

介绍完图的储存结构，接下来我们来了解一下图的最小生成树算法。

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。
若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。

3.1 Kruskal算法

Kruskal算法的思路是对每一次选择进行贪心：每次选取最短的一条边放入最小生成树中，并且要保证不成环:

1. 将所有的边压入优先队列中，按照小堆进行排序
2. 依次从队列中取出n个边
3. 通过并查集保证不成环，将取出的边的节点进行合并。
4. 将边加入到生成树中

//边
struct Edge
{size_t _srci;size_t _dsti;W _w;Edge(size_t src, size_t dst, const W& w):_srci(src), _dsti(dst), _w(w){}bool operator>(const Edge& e) const{return _w > e._w;}};W Kruskal(Self& minTree) {//算法核心思想//将所有的边放入堆中 从其中依次取出top元素//对于取出的元素判断是否属于同一连通变量 避免成环//直到顶点取完//初始化生成树minTree._size = _size;minTree._vertexs.resize(_size, MAX_W);for (int i = 0; i < _size; i++) {minTree._vertexs[i] = _vertexs[i];minTree._vIndexs[_vertexs[i]] = i;minTree._indexVs[i] = _vertexs[i];}minTree._map.resize(_size, vector<W>(_size, MAX_W));//进行处理//将所有的边储存到优先队列中priority_queue<Edge, vector<Edge>, greater<Edge>> q;for (size_t i = 0; i < _size; i++) {for (size_t j = 0; j < _size; j++) {if (_map[i][j] != MAX_W)q.push(Edge(i, j, _map[i][j]));elsecontinue;}}//并查集UnionFindSet<size_t> ufs(_vertexs);//接下来对路径进行选取W total = W();int cnt = 1;while (cnt < _size && !q.empty()) {//取出一条边Edge e = q.top();q.pop();//判断两个顶点是否是同一个集合 不在才能处理 否则会成环if (ufs.FindRoot(_indexVs[e._srci]) != ufs.FindRoot(_indexVs[e._dsti])) {minTree._addEdge(e._srci, e._dsti, e._w);//并查集合并两个集合ufs.UnionT(_indexVs[e._srci], _indexVs[e._dsti]);cnt++;total += e._w;}}if (cnt == _size) {return total;}else {return W();}}

3.2 Prim算法

Prim算法的思路是对两个连通变量中的边进行贪心，每次转化一个节点。因为每次都是从两个连通组中进行选择，prim天然的就会避免生成环，同样因为要有一个初始连通组，所以要有一个初始节点

1. 首先将出发点放入连通组A ，并存入其关联的边到优先队列
2. 从队列中取出最短的边，且两个节点不是同一个连通组
3. 将新放入节点关联的边放入优先队列
4. 再次取出边，直到取出n个节点

W Prim(Self& minTree , const T& src) {//prim 算法的核心是对两个连通组选取最短边 直到全部节点都选完//初始化生成树minTree._size = _size;minTree._vertexs.resize(_size, MAX_W);for (int i = 0; i < _size; i++) {minTree._vertexs[i] = _vertexs[i];minTree._vIndexs[_vertexs[i]] = i;minTree._indexVs[i] = _vertexs[i];}minTree._map.resize(_size, vector<W>(_size, MAX_W));//两个连通组vector<bool> A(_size , false);vector<bool> B(_size , true);//将起始位置进行处理int cnt = 1;int total = 0;size_t srci = _vIndexs[src];A[srci] = true;B[srci] = false;priority_queue<Edge, vector<Edge>, greater<Edge>> q;for (size_t i = 0; i < _size; i++) {if (_map[srci][i] != MAX_W) {q.push(Edge(srci, i, _map[srci][i]));}}//每次取出一个最短的边while (cnt < _size && !q.empty()) {Edge e = q.top();q.pop();// 源节点在A 目标节点在Bif (A[e._srci] == true && B[e._dsti] == true) {A[e._dsti] = true;B[e._dsti] = false;minTree._addEdge(e._srci, e._dsti, e._w);cnt++;total += e._w;//将 e._dsti 关联的边都放入qfor (size_t i = 0; i < _size; i++) {if (_map[e._dsti][i] != MAX_W) {q.push(Edge(e._dsti, i, _map[e._dsti][i]));}}}}if (cnt == _size) {return total;}else {return W();}}

4 并查集

这里补充并查集的知识点。
在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find-set)。

比如有三个家庭共10人报名了旅行团，他们其中就可以划分为三个集合：

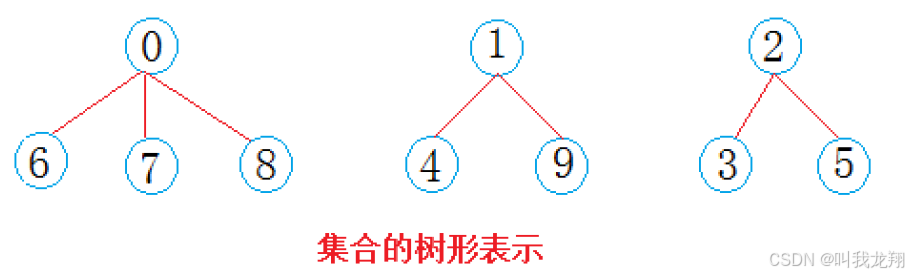
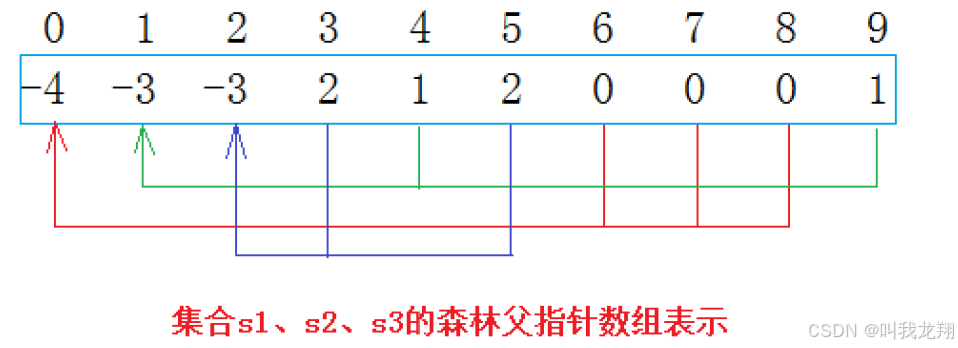
通过上面也可以看到并查集的特征

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素父节点在数组中的下标

这样通过一个数组就将不同的集合统计到了一起，接下来我们来实现一下并查集:

• 成员变量：节点-下标映射关系，节点数组，下标数组
• 寻找根节点函数 ， 这里加入路径压缩，可以避免大数量下的性能劣化。
• 合并两个集合函数

template<class T>
class UnionFindSet {
public://根据数组的构造(认为值可能出现重复的)template<class U>  // U推导为vector<T>&（左值）或vector<T>&&（右值）UnionFindSet(U&& v) {  // 万能引用//对数组进行去重set<T> tmp;for (size_t i = 0; i < v.size(); i++) {tmp.insert(v[i]);}//并查集的数据数量_size = tmp.size();//建立数组映射_parents.resize(_size, -1);//负值表示为根节点 非负值表示不是根节点//建立值与下标的映射关系//建立下标与值的映射关系size_t cnt = 0;for (auto& val : tmp) {_index[val] = cnt;_vals[cnt] = val;cnt += 1;}//初始化完成}size_t GetIndex(const T& val) {if (_index.empty() == true || _index.find(val) == _index.end()) {//cout << "[info] _index can not find val: " << val << endl;return -1;}return _index[val];}//获取该节点的根节点T FindRoot(const T& val) {//负数表示根节点size_t cur = GetIndex(val);//当前节点的下if (cur == -1) {return T();}while (_parents[cur] >= 0) {size_t p = _parents[cur];cur = p;}//找到根节点size_t root = cur;//压缩路径cur = GetIndex(val);while (_parents[cur] >= 0) {size_t p = _parents[cur];_parents[cur] = root;cur = p;}return _vals[root];}//获取该节点的根节点的下标size_t FindRootIndex(const T& val) {//负数表示根节点size_t cur = GetIndex(val);//当前节点的下标while (_parents[cur] >= 0) {size_t p = _parents[cur];cur = p;}//找到根节点size_t root = cur;//压缩路径cur = GetIndex(val);while (_parents[cur] >= 0) {size_t p = _parents[cur];_parents[cur] = root;cur = p;}return root;}//插入关系void Set(const T& t1, const T& t2) {//首先判断两者是否属于同一个集合size_t root1 = FindRootIndex(t1);size_t root2 = FindRootIndex(t2);Union(root1, root2);}//合并两个集合void Union(size_t root1, size_t root2) {if (root1 >= 0 || root2 >= 0){cout << "[warning] 非根节点参数的合并" << endl;return;}if (root1 == root2)return;//不是一个集合需要进行合并//合并将小集合合并到大集合中if ( abs(_parents[root1]) < abs(_parents[root2]) ) {swap(root1, root2);}_parents[root1] += _parents[root2];//将root2的数据量放入root1中_parents[root2] = root1;//root2指向root1}void UnionT(const T& t1, const T& t2) {//不是一个集合需要进行合并//合并将小集合合并到大集合中//找到根节点size_t root1 = FindRootIndex(t1);size_t root2 = FindRootIndex(t2);if (root1 == root2)return;if (abs(_parents[root1]) < abs(_parents[root2])) {swap(root1, root2);}_parents[root1] += _parents[root2];//将root2的数据量放入root1中_parents[root2] = root1;//root2指向root1}//判断是否属于同一个集合bool IsConnected(const T& t1, const T& t2) {//首先判断两者是否属于同一个集合size_t root1 = FindRootIndex(t1);size_t root2 = FindRootIndex(t2);if (root1 == root2)return true;elsereturn false;}private:vector<int> _parents; //储存下标 值表示头结点是谁unordered_map<T, size_t> _index; //储存值与下标的映射关系unordered_map<size_t , T> _vals;  //下标与储存值的映射关系size_t _size;
};