MATLAB实现决策树数值预测

MATLAB实现决策树数值预测

1.决策树数值预测

决策树数值预测是一种基于树状结构的回归方法，用于解决连续数值的预测问题。与分类树不同，回归树的目标变量是连续型数值而非离散类别。

其核心原理是通过递归地将特征空间划分为多个矩形区域，每个叶节点代表一个预测数值。构建过程中，算法寻找最优的特征和分割点，使得分裂后的子集内样本值的方差最小化。常用的分裂标准包括均方误差(MSE)最小化或平均绝对误差(MAE)最小化。

决策树回归的主要优势在于模型直观易懂，能够处理非线性关系，不需要特征标准化，且能自动处理特征交互作用。然而，单一决策树容易过拟合，对训练数据敏感。为提升性能，常采用剪枝技术控制树深度，或使用集成方法如随机森林和梯度提升树。

在实际应用中，决策树数值预测广泛应用于房价预测、销量 forecasting、股票价格预测等领域，为复杂回归问题提供可解释的解决方案。

2.MATLAB代码

%% 完全自写决策树回归算法clc;close all;clear all;warning off;%清除变量%% 1. 生成模拟数据
fprintf('生成模拟数据...\n');
rng(42);  % 设置随机种子n_samples = 500;
X1 = 8 * rand(n_samples, 1) + 2;  % 特征1: 2-10
X2 = 6 * rand(n_samples, 1) + 1;  % 特征2: 1-7% 创建有规律的目标变量
y_base = 20;
y_linear = 5 * X1 + 3 * X2;
y_nonlinear = 2 * X1.^2 + 1.5 * sin(2 * X2);
y_interaction = 0.8 * X1 .* X2;
noise = 3 * randn(n_samples, 1);y = y_base + y_linear + y_nonlinear + y_interaction + noise;% 组合特征
X = [X1, X2];
feature_names = {'特征1', '特征2'};fprintf('数据生成完成！样本数: %d\n', n_samples);%% 2. 决策树核心函数% 计算均方误差函数
function mse = calculate_mse(y)if isempty(y)mse = 0;elsemse = mean((y - mean(y)).^2);end
end% 寻找最佳分裂函数
function [best_feature, best_threshold, best_mse] = find_best_split(X, y, min_samples_leaf)n_features = size(X, 2);n_samples = length(y);%%
加我q1579325979 获取完整代码
%%for feature = 1:n_features% 对当前特征的所有可能值进行排序feature_values = unique(X(:, feature));for i = 1:length(feature_values)-1% 尝试相邻值的中间值作为阈值threshold = (feature_values(i) + feature_values(i+1)) / 2;% 根据阈值划分数据left_mask = X(:, feature) <= threshold;right_mask = ~left_mask;% 检查划分后的样本数if sum(left_mask) < min_samples_leaf || sum(right_mask) < min_samples_leafcontinue;end% 计算划分后的MSEleft_mse = calculate_mse(y(left_mask));right_mse = calculate_mse(y(right_mask));% 加权MSEtotal_mse = (sum(left_mask) * left_mse + sum(right_mask) * right_mse) / n_samples;% 更新最佳分裂if total_mse < best_msebest_mse = total_mse;best_feature = feature;best_threshold = threshold;endendend
end% 构建决策树函数
function node = build_tree(X, y, depth, max_depth, min_samples_split, min_samples_leaf)% 创建节点结构node = struct();node.is_leaf = false;node.prediction = mean(y);node.samples = length(y);node.mse = calculate_mse(y);% 停止条件检查if depth >= max_depth || ...length(y) < min_samples_split || ...calculate_mse(y) < 1e-6node.is_leaf = true;return;end% 寻找最佳分裂[best_feature, best_threshold, best_mse] = find_best_split(X, y, min_samples_leaf);if isempty(best_feature)node.is_leaf = true;return;end% 根据最佳分裂划分数据left_mask = X(:, best_feature) <= best_threshold;right_mask = ~left_mask;% 检查分裂后的样本数是否满足要求if sum(left_mask) < min_samples_leaf || sum(right_mask) < min_samples_leafnode.is_leaf = true;return;end% 递归构建左右子树node.is_leaf = false;node.feature_idx = best_feature;node.threshold = best_threshold;node.left_child = build_tree(X(left_mask, :), y(left_mask), depth + 1, max_depth, min_samples_split, min_samples_leaf);node.right_child = build_tree(X(right_mask, :), y(right_mask), depth + 1, max_depth, min_samples_split, min_samples_leaf);
end% 预测函数
function prediction = predict_tree(node, x)% 递归预测if node.is_leafprediction = node.prediction;elseif x(node.feature_idx) <= node.thresholdprediction = predict_tree(node.left_child, x);elseprediction = predict_tree(node.right_child, x);endend
end% 批量预测函数
function predictions = predict_batch(tree, X)n_samples = size(X, 1);predictions = zeros(n_samples, 1);for i = 1:n_samplespredictions(i) = predict_tree(tree, X(i, :));end
end% 打印树结构函数
function print_tree_structure(node, depth, feature_names)indent = repmat('  ', 1, depth);if node.is_leaffprintf('%s叶节点: 预测值=%.2f, 样本数=%d, MSE=%.2f\n', ...indent, node.prediction, node.samples, node.mse);elsefeature_name = '未知特征';if ~isempty(feature_names) && node.feature_idx <= length(feature_names)feature_name = feature_names{node.feature_idx};endfprintf('%s决策节点: %s <= %.2f, 样本数=%d, MSE=%.2f\n', ...indent, feature_name, node.threshold, node.samples, node.mse);fprintf('%s左子树:\n', indent);print_tree_structure(node.left_child, depth + 1, feature_names);fprintf('%s右子树:\n', indent);print_tree_structure(node.right_child, depth + 1, feature_names);end
end%% 3. 数据可视化 - 原始数据分布
figure('Position', [100, 100, 1200, 800]);% 图1: 原始数据三维散点图
subplot(2, 3, 1);
scatter3(X1, X2, y, 40, y, 'filled');
xlabel('特征1');
ylabel('特征2');
zlabel('目标值');
title('原始数据三维分布');
colorbar;
grid on;% 图2: 特征1与目标值关系
subplot(2, 3, 2);
scatter(X1, y, 30, 'filled', 'MarkerFaceAlpha', 0.6);
xlabel('特征1');
ylabel('目标值');
title('特征1 vs 目标值');
grid on;% 图3: 特征2与目标值关系
subplot(2, 3, 3);
scatter(X2, y, 30, 'filled', 'MarkerFaceAlpha', 0.6);
xlabel('特征2');
ylabel('目标值');
title('特征2 vs 目标值');
grid on;% 图4: 目标值分布直方图
subplot(2, 3, 4);
histogram(y, 20, 'FaceColor', 'blue', 'FaceAlpha', 0.7);
xlabel('目标值');
ylabel('频数');
title('目标值分布');
grid on;% 图5: 特征分布箱线图
subplot(2, 3, 5);
boxplot(X, 'Labels', feature_names);
ylabel('特征值');
title('特征分布箱线图');
grid on;% 图6: 特征散点图矩阵
subplot(2, 3, 6);
scatter(X1, X2, 30, y, 'filled');
xlabel('特征1');
ylabel('特征2');
title('特征散点图（颜色表示目标值）');
colorbar;
grid on;sgtitle('原始数据可视化分析', 'FontSize', 14, 'FontWeight', 'bold');%% 4. 数据分割
fprintf('\n数据分割...\n');
train_ratio = 0.7;
n_train = round(train_ratio * n_samples);shuffle_idx = randperm(n_samples);
X_train = X(shuffle_idx(1:n_train), :);
y_train = y(shuffle_idx(1:n_train));
X_test = X(shuffle_idx(n_train+1:end), :);
y_test = y(shuffle_idx(n_train+1:end));fprintf('训练集: %d 样本\n', n_train);
fprintf('测试集: %d 样本\n', n_samples - n_train);%% 5. 训练自写决策树模型
fprintf('\n训练自写决策树模型...\n');% 设置决策树参数
max_depth = 5;
min_samples_split = 10;
min_samples_leaf = 5;% 训练模型
tic;
decision_tree = build_tree(X_train, y_train, 0, max_depth, min_samples_split, min_samples_leaf);
training_time = toc;fprintf('模型训练完成！训练时间: %.2f 秒\n', training_time);% 打印树结构
fprintf('\n决策树结构:\n');
print_tree_structure(decision_tree, 0, feature_names);%% 6. 模型预测和评估
fprintf('\n模型预测和评估...\n');% 预测
y_pred_train = predict_batch(decision_tree, X_train);
y_pred_test = predict_batch(decision_tree, X_test);% 计算评估指标
mse_train = mean((y_train - y_pred_train).^2);
mse_test = mean((y_test - y_pred_test).^2);rmse_train = sqrt(mse_train);
rmse_test = sqrt(mse_test);mae_train = mean(abs(y_train - y_pred_train));
mae_test = mean(abs(y_test - y_pred_test));r2_train = 1 - sum((y_train - y_pred_train).^2) / sum((y_train - mean(y_train)).^2);
r2_test = 1 - sum((y_test - y_pred_test).^2) / sum((y_test - mean(y_test)).^2);fprintf('\n=== 模型性能评估 ===\n');
fprintf('训练集 - RMSE: %.3f, MAE: %.3f, R²: %.3f\n', rmse_train, mae_train, r2_train);
fprintf('测试集 - RMSE: %.3f, MAE: %.3f, R²: %.3f\n', rmse_test, mae_test, r2_test);%% 7. 结果可视化
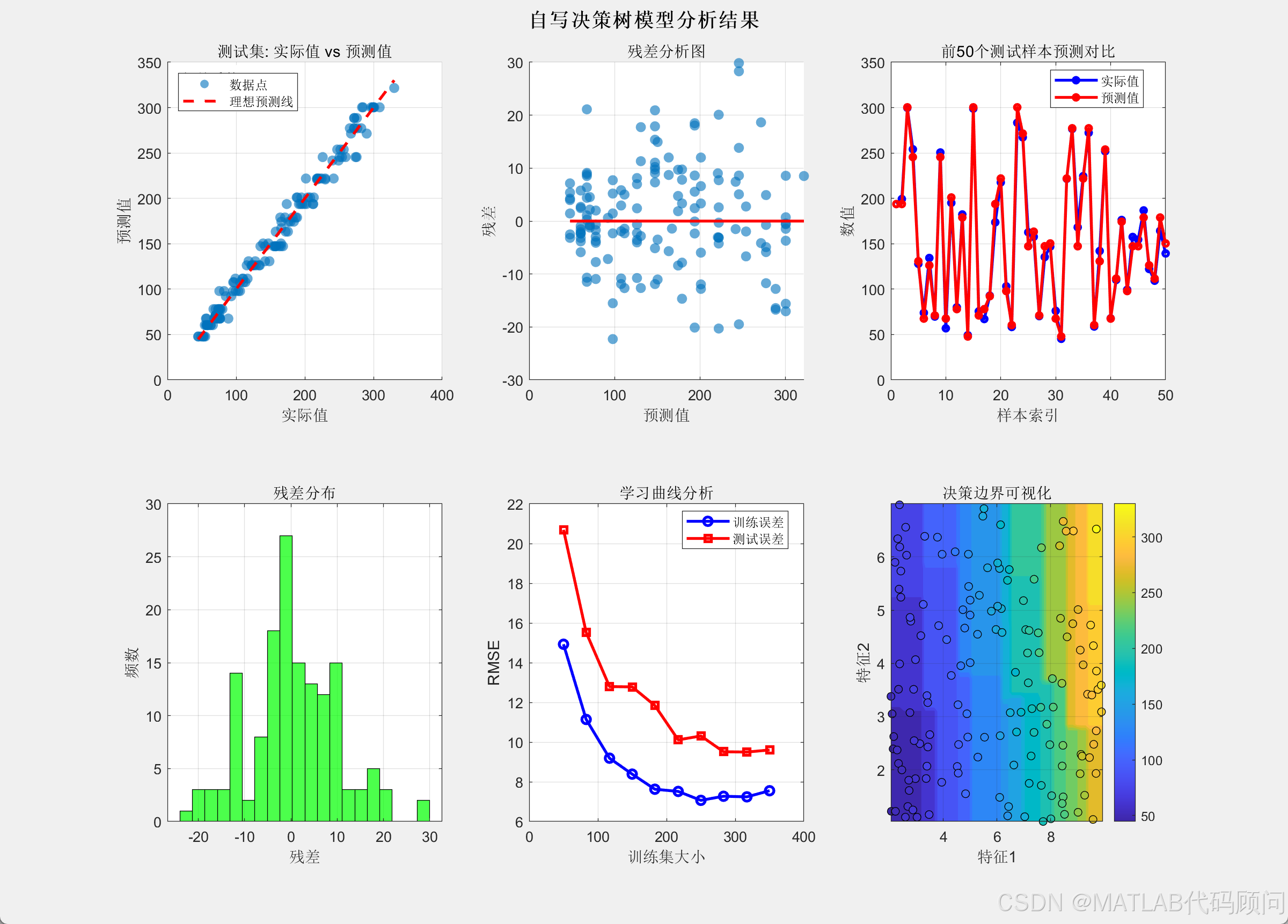
figure('Position', [100, 100, 1200, 900]);% 图1: 实际值 vs 预测值散点图
subplot(2, 3, 1);
scatter(y_test, y_pred_test, 50, 'filled', 'MarkerFaceAlpha', 0.6);
hold on;
plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], 'r--', 'LineWidth', 2);
xlabel('实际值');
ylabel('预测值');
title('测试集: 实际值 vs 预测值');
legend('数据点', '理想预测线', 'Location', 'northwest');
grid on;% 添加相关系数
corr_coef = corr(y_test, y_pred_test);
text(0.05, 0.95, sprintf('相关系数: %.3f', corr_coef), ...'Units', 'normalized', 'FontSize', 10, 'BackgroundColor', 'white');% 图2: 残差分析
subplot(2, 3, 2);
residuals = y_test - y_pred_test;
scatter(y_pred_test, residuals, 50, 'filled', 'MarkerFaceAlpha', 0.6);
hold on;
plot([min(y_pred_test), max(y_pred_test)], [0, 0], 'r-', 'LineWidth', 2);
xlabel('预测值');
ylabel('残差');
title('残差分析图');
grid on;% 图3: 预测趋势对比
subplot(2, 3, 3);
sample_indices = 1:min(50, length(y_test));
plot(sample_indices, y_test(sample_indices), 'bo-', 'LineWidth', 2, 'MarkerSize', 4);
hold on;
plot(sample_indices, y_pred_test(sample_indices), 'ro-', 'LineWidth', 2, 'MarkerSize', 4);
xlabel('样本索引');
ylabel('数值');
title('前50个测试样本预测对比');
legend('实际值', '预测值', 'Location', 'best');
grid on;% 图4: 误差分布
subplot(2, 3, 4);
histogram(residuals, 20, 'FaceColor', 'green', 'FaceAlpha', 0.7);
xlabel('残差');
ylabel('频数');
title('残差分布');
grid on;% 图5: 学习曲线分析
subplot(2, 3, 5);
train_sizes = round(linspace(50, n_train, 10));
train_errors = zeros(length(train_sizes), 1);
test_errors = zeros(length(train_sizes), 1);for i = 1:length(train_sizes)current_size = train_sizes(i);temp_tree = build_tree(X_train(1:current_size, :), y_train(1:current_size), 0, max_depth, min_samples_split, min_samples_leaf);temp_train_pred = predict_batch(temp_tree, X_train(1:current_size, :));train_errors(i) = sqrt(mean((y_train(1:current_size) - temp_train_pred).^2));temp_test_pred = predict_batch(temp_tree, X_test);test_errors(i) = sqrt(mean((y_test - temp_test_pred).^2));
endplot(train_sizes, train_errors, 'b-o', 'LineWidth', 2);
hold on;
plot(train_sizes, test_errors, 'r-s', 'LineWidth', 2);
xlabel('训练集大小');
ylabel('RMSE');
title('学习曲线分析');
legend('训练误差', '测试误差', 'Location', 'best');
grid on;% 图6: 决策边界可视化
subplot(2, 3, 6);
[x1_grid, x2_grid] = meshgrid(linspace(min(X(:,1)), max(X(:,1)), 50), ...linspace(min(X(:,2)), max(X(:,2)), 50));
X_grid = [x1_grid(:), x2_grid(:)];
y_grid_pred = predict_batch(decision_tree, X_grid);
y_grid_pred = reshape(y_grid_pred, size(x1_grid));contourf(x1_grid, x2_grid, y_grid_pred, 20, 'LineColor', 'none');
hold on;
scatter(X_test(:,1), X_test(:,2), 30, y_test, 'filled', 'MarkerEdgeColor', 'k');
xlabel('特征1');
ylabel('特征2');
title('决策边界可视化');
colorbar;
grid on;sgtitle('自写决策树模型分析结果', 'FontSize', 14, 'FontWeight', 'bold');%% 8. 模型深度和复杂度分析
fprintf('\n模型复杂度分析...\n');% 测试不同最大深度对性能的影响
max_depths = 2:8;
train_scores = zeros(length(max_depths), 1);
test_scores = zeros(length(max_depths), 1);for i = 1:length(max_depths)depth = max_depths(i);temp_tree = build_tree(X_train, y_train, 0, depth, min_samples_split, min_samples_leaf);y_pred_train_temp = predict_batch(temp_tree, X_train);y_pred_test_temp = predict_batch(temp_tree, X_test);train_scores(i) = 1 - sum((y_train - y_pred_train_temp).^2) / sum((y_train - mean(y_train)).^2);test_scores(i) = 1 - sum((y_test - y_pred_test_temp).^2) / sum((y_test - mean(y_test)).^2);
endfigure('Position', [100, 100, 800, 400]);
plot(max_depths, train_scores, 'b-o', 'LineWidth', 2, 'MarkerSize', 6);
hold on;
plot(max_depths, test_scores, 'r-s', 'LineWidth', 2, 'MarkerSize', 6);
xlabel('决策树最大深度');
ylabel('R² 决定系数');
title('模型复杂度分析');
legend('训练集R²', '测试集R²', 'Location', 'best');
grid on;fprintf('\n不同深度下的R²得分:\n');
for i = 1:length(max_depths)fprintf('深度 %d: 训练集R²=%.3f, 测试集R²=%.3f\n', ...max_depths(i), train_scores(i), test_scores(i));
end%% 9. 新样本预测示例
fprintf('\n=== 新样本预测示例 ===\n');
new_samples = [5, 3; 7, 2; 3, 5];
for i = 1:size(new_samples, 1)prediction = predict_tree(decision_tree, new_samples(i, :));fprintf('新样本 %d: 特征1=%.1f, 特征2=%.1f => 预测值=%.2f\n', ...i, new_samples(i,1), new_samples(i,2), prediction);
endfprintf('\n=== 程序执行完成 ===\n');

3.程序结果

生成模拟数据...
数据生成完成！样本数: 500

数据分割...
训练集: 350 样本
测试集: 150 样本

训练自写决策树模型...
模型训练完成！训练时间: 0.03 秒

决策树结构:
决策节点: 特征1 <= 6.55, 样本数=350, MSE=6052.76
左子树:
决策节点: 特征1 <= 4.54, 样本数=191, MSE=1249.23
左子树:
决策节点: 特征1 <= 3.27, 样本数=109, MSE=357.04
左子树:
决策节点: 特征2 <= 3.11, 样本数=56, MSE=108.86
左子树:
决策节点: 特征1 <= 2.38, 样本数=25, MSE=45.24
左子树:
叶节点: 预测值=47.81, 样本数=6, MSE=12.16
右子树:
叶节点: 预测值=60.36, 样本数=19, MSE=17.90
右子树:
决策节点: 特征2 <= 5.29, 样本数=31, MSE=60.92
左子树:
叶节点: 预测值=67.54, 样本数=17, MSE=35.45
右子树:
叶节点: 预测值=77.98, 样本数=14, MSE=32.08
右子树:
决策节点: 特征2 <= 3.21, 样本数=53, MSE=153.74
左子树:
决策节点: 特征1 <= 3.75, 样本数=21, MSE=112.83
左子树:
叶节点: 预测值=71.01, 样本数=5, MSE=7.73
右子树:
叶节点: 预测值=92.21, 样本数=16, MSE=38.66
右子树:
决策节点: 特征2 <= 5.86, 样本数=32, MSE=101.21
左子树:
叶节点: 预测值=97.88, 样本数=24, MSE=52.48
右子树:
叶节点: 预测值=111.60, 样本数=8, MSE=106.36
右子树:
决策节点: 特征1 <= 6.12, 样本数=82, MSE=423.47
左子树:
决策节点: 特征1 <= 5.01, 样本数=62, MSE=241.53
左子树:
决策节点: 特征2 <= 3.82, 样本数=23, MSE=129.24
左子树:
叶节点: 预测值=107.65, 样本数=9, MSE=52.11
右子树:
叶节点: 预测值=126.21, 样本数=14, MSE=43.93
右子树:
决策节点: 特征2 <= 3.73, 样本数=39, MSE=161.66
左子树:
叶节点: 预测值=130.73, 样本数=20, MSE=90.61
右子树:
叶节点: 预测值=147.29, 样本数=19, MSE=95.78
右子树:
决策节点: 特征2 <= 3.24, 样本数=20, MSE=136.94
左子树:
叶节点: 预测值=150.35, 样本数=6, MSE=55.54
右子树:
决策节点: 特征2 <= 4.76, 样本数=14, MSE=41.01
左子树:
叶节点: 预测值=167.12, 样本数=6, MSE=14.48
右子树:
叶节点: 预测值=174.32, 样本数=8, MSE=38.71
右子树:
决策节点: 特征1 <= 8.64, 样本数=159, MSE=2000.36
左子树:
决策节点: 特征1 <= 7.55, 样本数=95, MSE=720.27
左子树:
决策节点: 特征2 <= 3.46, 样本数=46, MSE=283.83
左子树:
决策节点: 特征1 <= 7.03, 样本数=18, MSE=118.86
左子树:
叶节点: 预测值=163.36, 样本数=7, MSE=67.58
右子树:
叶节点: 预测值=178.94, 样本数=11, MSE=57.15
右子树:
决策节点: 特征2 <= 5.61, 样本数=28, MSE=111.66
左子树:
叶节点: 预测值=193.77, 样本数=15, MSE=46.87
右子树:
叶节点: 预测值=206.21, 样本数=13, MSE=103.53
右子树:
决策节点: 特征2 <= 3.62, 样本数=49, MSE=343.79
左子树:
决策节点: 特征1 <= 8.03, 样本数=18, MSE=133.21
左子树:
叶节点: 预测值=201.02, 样本数=8, MSE=21.33
右子树:
叶节点: 预测值=221.89, 样本数=10, MSE=29.18
右子树:
决策节点: 特征1 <= 7.74, 样本数=31, MSE=207.44
左子树:
叶节点: 预测值=220.87, 样本数=8, MSE=33.21
右子树:
叶节点: 预测值=245.51, 样本数=23, MSE=111.32
右子树:
决策节点: 特征2 <= 2.80, 样本数=64, MSE=581.65
左子树:
决策节点: 特征1 <= 9.33, 样本数=19, MSE=271.74
左子树:
决策节点: 特征1 <= 9.12, 样本数=12, MSE=58.83
左子树:
叶节点: 预测值=241.70, 样本数=6, MSE=31.81
右子树:
叶节点: 预测值=253.85, 样本数=6, MSE=11.99
右子树:
叶节点: 预测值=277.25, 样本数=7, MSE=87.92
右子树:
决策节点: 特征1 <= 9.37, 样本数=45, MSE=313.18
左子树:
决策节点: 特征1 <= 8.92, 样本数=22, MSE=147.91
左子树:
叶节点: 预测值=271.41, 样本数=8, MSE=36.92
右子树:
叶节点: 预测值=288.53, 样本数=14, MSE=104.79
右子树:
决策节点: 特征2 <= 5.05, 样本数=23, MSE=154.58
左子树:
叶节点: 预测值=300.36, 样本数=15, MSE=60.07
右子树:
叶节点: 预测值=321.62, 样本数=8, MSE=37.09

模型预测和评估...

=== 模型性能评估 ===
训练集 - RMSE: 7.551, MAE: 5.939, R²: 0.991
测试集 - RMSE: 9.604, MAE: 7.409, R²: 0.985

模型复杂度分析...

不同深度下的R²得分:
深度 2: 训练集R²=0.915, 测试集R²=0.912
深度 3: 训练集R²=0.962, 测试集R²=0.950
深度 4: 训练集R²=0.981, 测试集R²=0.975
深度 5: 训练集R²=0.991, 测试集R²=0.985
深度 6: 训练集R²=0.994, 测试集R²=0.990
深度 7: 训练集R²=0.995, 测试集R²=0.990
深度 8: 训练集R²=0.995, 测试集R²=0.990

=== 新样本预测示例 ===
新样本 1: 特征1=5.0, 特征2=3.0 => 预测值=107.65
新样本 2: 特征1=7.0, 特征2=2.0 => 预测值=163.36
新样本 3: 特征1=3.0, 特征2=5.0 => 预测值=67.54

=== 程序执行完成 ===
>> 

4.代码、程序订制(MATLAB、Python) →QQ:1579325979

4.1 各类智能算法

中文名称	英文全称	缩写	出现年份
遗传算法	Genetic Algorithm	GA	1975
粒子群优化算法	Particle Swarm Optimization	PSO	1995
蚁群优化算法	Ant Colony Optimization	ACO	1992
模拟退火算法	Simulated Annealing	SA	1983
免疫优化算法	Immune Optimization Algorithm	IA	1986
贪婪算法	Greedy Algorithm	-	1970
差分进化算法	Differential Evolution	DE	1997
混合蛙跳算法	Shuffled Frog Leaping Algorithm	SFLA	2003
人工蜂群算法	Artificial Bee Colony	ABC	2005
人工鱼群算法	Artificial Fish Swarm Algorithm	AFSA	2002
萤火虫算法	Glowworm Swarm Optimization	GSO	2005
果蝇优化算法	Fruit Fly Optimization Algorithm	FOA	2011
布谷鸟搜索算法	Cuckoo Search	CS	2009
猴群算法	Monkey Algorithm	MA	2008
免疫网络算法	Immune Network Algorithm	aiNet	2000
水滴算法	Intelligent Water Drops Algorithm	IWD	2007
和声搜索算法	Harmony Search	HS	2001
克隆选择算法	Clonal Selection Algorithm	CLONALG	2000
禁忌搜索算法	Tabu Search	TS	1986
爬山算法	Hill Climbing	HC	1940
引力搜索算法	Gravitational Search Algorithm	GSA	2009
细菌觅食优化算法	Bacterial Foraging Optimization	BFO	2002
蝙蝠算法	Bat Algorithm	BA	2010
邻域搜索算法	Neighborhood Search	NS	1960
变邻域搜索算法	Variable Neighborhood Search	VNS	1997
蜜蜂交配优化算法	Honey Bees Mating Optimization	HBMO	2001
文化基因算法	Memetic Algorithm	MA	1989
烟花算法	Fireworks Algorithm	FWA	2010
思维进化算法	Mind Evolutionary Algorithm	MEA	1998
蜻蜓算法	Dragonfly Algorithm	DA	2016
虚拟力场算法	Virtual Force Field Algorithm	VFF	1989
遗传规划	Genetic Programming	GP	1992
鲸鱼优化算法	Whale Optimization Algorithm	WOA	2016
灰狼优化算法	Grey Wolf Optimizer	GWO	2014
狼群算法	Wolf Pack Algorithm	WPA	2007
鸡群优化算法	Chicken Swarm Optimization	CSO	2014
生物地理学优化算法	Biogeography-Based Optimization	BBO	2008
分布估计算法	Estimation of Distribution Algorithm	EDA	1996
帝国竞争算法	Imperialist Competitive Algorithm	ICA	2007
天牛须搜索算法	Beetle Antennae Search Algorithm	BAS	2017
头脑风暴优化算法	Brain Storm Optimization	BSO	2011
人工势场法	Artificial Potential Field	APF	1986
猫群算法	Cat Swarm Optimization	CSO	2006
蚁狮优化算法	Ant Lion Optimizer	ALO	2015
飞蛾火焰优化算法	Moth-Flame Optimization	MFO	2015
蘑菇繁殖优化算法	Mushroom Reproduction Optimization	MRO	2020
麻雀搜索算法	Sparrow Search Algorithm	SSA	2020
水波优化算法	Water Wave Optimization	WWO	2015
斑鬣狗优化算法	Spotted Hyena Optimizer	SHO	2017
雪融优化算法	Snow Ablation Optimization	SAO	2022
蝴蝶优化算法	Butterfly Optimization Algorithm	BOA	2019
磷虾群算法	Krill Herd Algorithm	KHA	2012
黏菌算法	Slime Mould Algorithm	SMA	2020
人类学习优化算法	Human Learning Optimization	HLO	2014
母亲优化算法	Mother Optimization Algorithm	MOA	2023

4.2各类优化问题

各种优化课题	各种优化课题
车间调度	路由路网优化
机场调度	顺序约束项目调度
工程项目调度	双层规划
港口调度	零件拆卸装配问题优化
生产线平衡问题	水资源调度
用电调度	库位优化
公交车发车调度	库位路线优化
车辆路径物流配送优化	武器分配优化
选址配送优化	覆盖问题优化
物流公铁水问题优化	管网问题优化
供应链、生产计划、库存优化	PID优化
库位优化、货位优化	VMD优化

4.3各类神经网络、深度学习、机器学习

序号	模型名称	核心特点	适用场景
1	BiLSTM 双向长短时记忆神经网络分类	双向捕捉序列上下文信息	自然语言处理、语音识别
2	BP 神经网络分类	误差反向传播训练	通用分类任务
3	CNN 卷积神经网络分类	自动提取空间特征	图像、视频分类
4	DBN 深度置信网络分类	多层受限玻尔兹曼机堆叠	特征学习、降维
5	DELM 深度学习极限学习机分类	结合 ELM 与深度架构	复杂分类任务
6	ELMAN 递归神经网络分类	含反馈连接的递归结构	时间序列、语音
7	ELM 极限学习机分类	随机生成隐藏层，快速训练	小样本学习
8	GRNN 广义回归神经网络分类	基于径向基函数回归	函数逼近、时间序列
9	GRU 门控循环单元分类	门控机制简化 LSTM	序列建模
10	KELM 混合核极限学习机分类	结合多核 ELM	高维复杂数据
11	KNN 分类	基于距离的分类方法	模式识别
12	LSSVM 最小二乘法支持向量机分类	最小二乘优化 SVM	小样本分类
13	LSTM 长短时记忆网络分类	门控机制处理长期依赖	语言建模
14	MLP 全连接神经网络分类	多层感知机	通用分类
15	PNN 概率神经网络分类	基于贝叶斯原理	模式识别
16	RELM 鲁棒极限学习机分类	增强鲁棒性的 ELM	噪声数据
17	RF 随机森林分类	多棵决策树集成	高维、非线性数据
18	SCN 随机配置网络模型分类	随机生成网络结构	快速训练
19	SVM 支持向量机分类	寻找最优分类超平面	二分类、多分类
20	XGBOOST 分类	梯度提升决策树	大规模结构化数据
21	ANFIS 自适应模糊神经网络预测	融合模糊逻辑与神经网络	复杂非线性系统建模
22	ANN 人工神经网络预测	多层神经元网络	通用预测任务
23	ARMA 自回归滑动平均模型预测	线性时间序列建模	时间序列预测
24	BF 粒子滤波预测	基于蒙特卡洛采样	动态系统状态估计
25	BiLSTM 双向长短时记忆神经网络预测	双向捕捉序列信息	时间序列、文本预测
26	BLS 宽度学习神经网络预测	增量学习结构	在线学习
27	BP 神经网络预测	误差反向传播训练	通用预测
28	CNN 卷积神经网络预测	自动特征提取	图像、视频预测
29	DBN 深度置信网络预测	多层无监督预训练	特征学习预测
30	DELM 深度学习极限学习机预测	结合 ELM 与深度结构	复杂预测任务
31	DKELM 回归预测	动态核 ELM 回归	时间序列回归
32	ELMAN 递归神经网络预测	递归结构处理时序	时间序列
33	ELM 极限学习机预测	快速训练	小样本回归
34	ESN 回声状态网络预测	储备池计算	时间序列预测
35	FNN 前馈神经网络预测	前向传播	通用预测
36	GMDN 预测	基因表达数据网络建模	生物信息学预测
37	GMM 高斯混合模型预测	多高斯分布建模	密度估计、聚类
38	GRNN 广义回归神经网络预测	径向基函数回归	函数逼近
39	GRU 门控循环单元预测	门控机制简化 LSTM	时间序列预测
40	KELM 混合核极限学习机预测	多核 ELM 回归	高维回归
41	LMS 最小均方算法预测	线性回归的迭代优化	自适应滤波
42	LSSVM 最小二乘法支持向量机预测	最小二乘优化 SVM	回归预测
43	LSTM 长短时记忆网络预测	门控处理长期依赖	时间序列预测
44	RBF 径向基函数神经网络预测	径向基函数逼近	函数拟合
45	RELM 鲁棒极限学习机预测	增强鲁棒性的 ELM	噪声数据回归
46	RF 随机森林预测	决策树集成	回归预测
47	RNN 循环神经网络预测	循环连接处理序列	时间序列预测
48	RVM 相关向量机预测	稀疏贝叶斯学习	回归、分类
49	SVM 支持向量机预测	寻找最优超平面	回归预测
50	TCN 时间卷积神经网络预测	一维卷积处理时序	时间序列预测
51	XGBoost 回归预测	梯度提升决策树	大规模回归