用Python来学微积分35-变上限定积分

变上限积分是微积分学中的核心概念，它不仅在理论上是微积分基本定理的重要组成部分，也在实际计算中发挥着关键作用。本文将系统阐述变上限积分的定义、性质及其应用，通过理论推导与实例分析相结合的方式，帮助读者深入理解这一概念。

一、变上限积分函数的定义

1.1 数学定义

设函数 $f(x)$ 在区间 $[a,b]$ 上可积，则对任意的 $x\in [a,b]$，定积分 ${\int }_a^{x}f(t)dt$ 在 $[a,b]$ 上定义了一个函数，称为变上限积分函数，记作 $F(x)$。即：

$$F(x)={\int }_a^{x}f(t)dt(a\le x\le b)$$

从几何意义上看，若 $f(t)\ge 0$ ($t\in [a,b]$)，则 $F(x)$ 表示区间 $[a,x]$ 上以曲线 $y=f(x)$ 为曲边的曲边梯形的面积。随着上限 $x$ 的变化，积分区间 $[a,x]$ 随之改变，从而得到不同的积分值，这就是“变上限”的含义。

1.2 理解要点

关键认识：变上限积分本质是一个关于上限 $x$ 的函数，而不是一个固定的积分值。积分变量 $t$ 在积分过程中是“哑变量”，积分完成后整个表达式只与上限 $x$ 有关。

区分概念：变上限积分与普通定积分的区别在于，前者的上限是一个变量，而后者上下限都是常数。

1.3 手动求解示例

计算定积分 ${\int }_2^{x}t\sin (t)dt$。

步骤1 应用分部积分法

设：

• $u=t$, 则 $du=dt$
• $dv=\sin (t)dt$, 则 $v=-\cos (t)$

根据分部积分公式 $\int udv=uv-\int vdu$： $$\int t\sin (t)dt=-t\cos (t)-\int (-\cos (t))dt=-t\cos (t)+\int \cos (t)dt=-t\cos (t)+\sin (t)+C$$ 其中 $C$ 为积分常数。

步骤2. 计算定积分 $$\begin{array}{rl}F(x)& ={\int }_2^{x}t\sin (t)dt\\ & ={\left[-t\cos (t)+\sin (t)\right]}_2^x\\ & =\left(-x\cos (x)+\sin (x)\right)-\left(-2\cos (2)+\sin (2)\right)\\ & =-x\cos (x)+\sin (x)+2\cos (2)-\sin (2)\end{array}$$

1.4 Python代码示例

import sympy as sp# 定义符号变量
x, t = sp.symbols('x t')
# 假设被积函数 f(t)
f = t * sp.sin(t)
# 定义变上限积分函数 F(x)
F = sp.integrate(f, (t, 2, x))
print("变上限积分函数 F(x):", F)

执行结果：

变上限积分函数 F(x): -x*cos(x) + sin(x) - sin(2) + 2*cos(2)

二、变上限积分函数的连续性定理

2.1 数学表述

设函数 $f(x)$ 在区间 $[a,b]$ 上可积，则变上限积分函数 $F(x)={\int }_a^{x}f(t)dt$ 在 $[a,b]$ 上连续。

这一性质表明，即使被积函数 $f(x)$ 仅可积（不一定连续），其变上限积分函数 $F(x)$ 也总是连续的。这是积分运算的“平滑效应”——积分能改善函数的正则性。

2.2 证明思路

证明概要：

1. 考虑函数值的变化量：$\Delta F=F(x+\Delta x)-F(x)={\int }_x^{x+\Delta x}f(t)dt$
2. 由于 $f(x)$ 在 $[a,b]$ 上可积，故有界，即存在 $M>0$ 使得 $|f(x)|\le M$
3. 于是有：$|\Delta F|=\left|{\int }_x^{x+\Delta x}f(t)dt\right|\le M|\Delta x|$
4. 当 $\Delta x\to 0$ 时，$|\Delta F|\to 0$，故 $F(x)$ 连续

2.3 Python可视化验证

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad# 定义被积函数（含间断点仍可积）
def f(t):return 1 if t < 3 else 2  # 在t=3处有跳跃间断点# 定义变上限积分函数
def F(x):result, _ = quad(f, 2, x)return result# 生成x值
x_values = np.linspace(2, 5, 100)
# 计算对应的F(x)值
y_values = [F(x) for x in x_values]# 绘制函数图像
plt.figure(figsize=(10, 6))
plt.plot(x_values, y_values)
plt.xlabel('x')
plt.ylabel('F(x)')
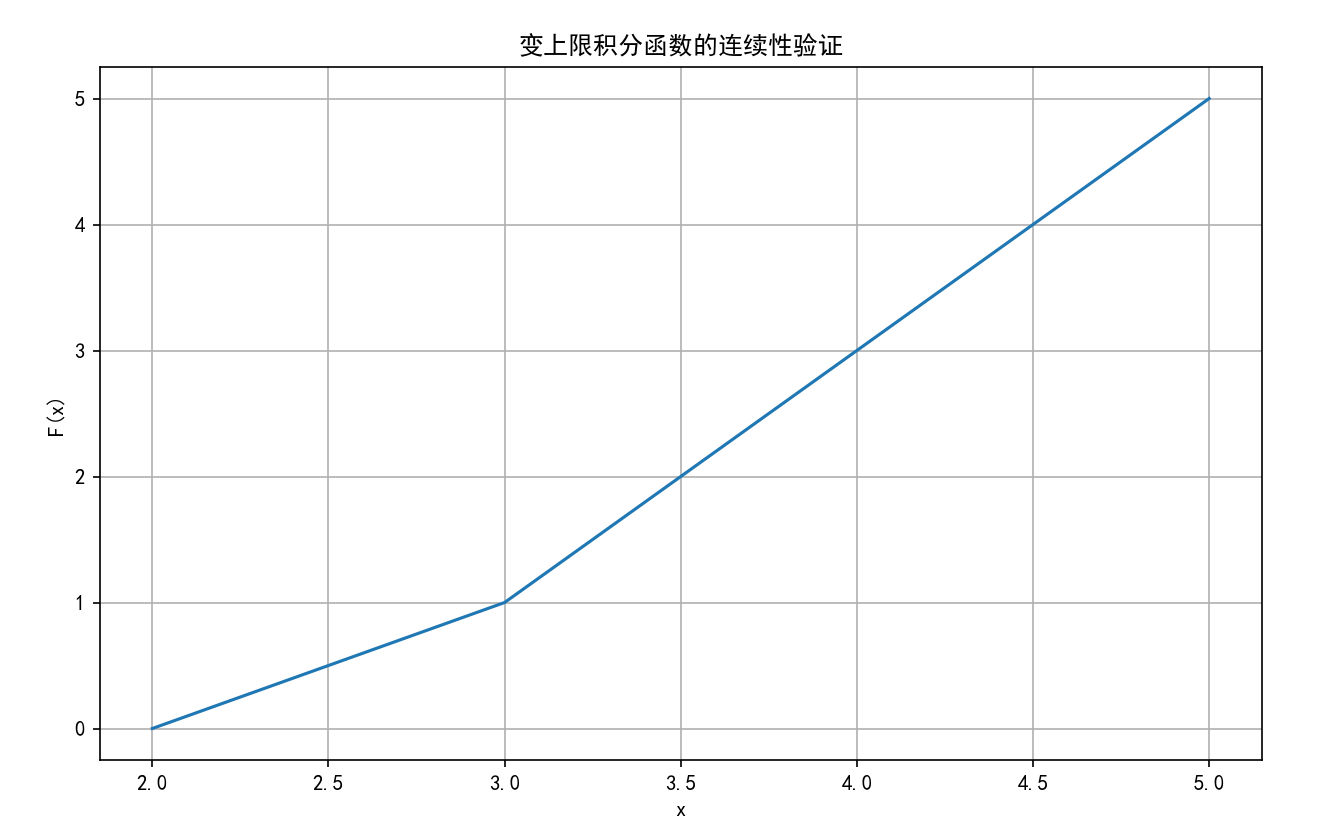
plt.title('变上限积分函数的连续性验证')
plt.grid(True)
plt.show()

执行后会显示一条连续曲线，尽管被积函数有间断点，但变上限积分函数仍然是连续的。

三、微积分基本定理（第一部分）

3.1 定理内容

设函数 $f(x)$ 在区间 $[a,b]$ 上连续，则变上限积分函数 $F(x)={\int }_a^{x}f(t)dt$ 在 $[a,b]$ 上可导，且：

$$F^{\prime }(x)=\frac{d}{dx}{\int }_a^{x}f(t)dt=f(x)(a\le x\le b)$$

这表明，对于连续函数，变上限积分是其一个原函数。这一定理建立了微分与积分之间的互逆关系，是微积分学的核心结果。

3.2 定理证明

证明过程：

1. 计算函数增量：设 $x\in (a,b)$，自变量有增量 $\Delta x$（使 $x+\Delta x\in (a,b)$），则函数增量为： $$\Delta F=F(x+\Delta x)-F(x)={\int }_x^{x+\Delta x}f(t)dt$$

2. 应用中值定理：由积分中值定理，存在 $\xi$ 介于 $x$ 与 $x+\Delta x$ 之间，使得： $${\int }_x^{x+\Delta x}f(t)dt=f(\xi )\Delta x$$

3. 求导数： $$F^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{\Delta F}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(\xi )\Delta x}{\Delta x}=\underset{\xi \to x}{\lim }f(\xi )=f(x)$$

最后一步成立是因为 $f(x)$ 连续。

3.3 Python验证

import sympy as sp# 定义符号变量
x, t = sp.symbols('x t')
# 定义连续函数 f(t)
f = sp.exp(t)  # 指数函数在定义域内连续
# 定义变上限积分函数 F(x)
F = sp.integrate(f, (t, 0, x))
# 对 F(x) 求导
F_prime = sp.diff(F, x)
print("F'(x) =", F_prime)
print("f(x) =", f.subs(t, x))

执行结果：

F'(x) = exp(x)
f(x) = exp(x)

结果验证了 $F^{\prime }(x)=f(x)$，与定理一致。

四、复合变上限积分的求导法则

4.1 一般形式

在实际问题中，积分上下限可能都是函数而非常数，此时需要更一般的求导公式：

1. 上限为函数：$\frac{d}{dx}\left[{\int }_a^{g(x)}f(t)dt\right]=f(g(x))\cdot g^{\prime }(x)$

2. 下限为函数：$\frac{d}{dx}\left[{\int }_{h(x)}^{a}f(t)dt\right]=-f(h(x))\cdot h^{\prime }(x)$

3. 上下限均为函数： $$\frac{d}{dx}\left[{\int }_{h(x)}^{g(x)}f(t)dt\right]=f(g(x))\cdot g^{\prime }(x)-f(h(x))\cdot h^{\prime }(x)$$

4.2 推导思路

以上下限均为函数的情况为例：

1. 令 $G(u,v)={\int }_v^{u}f(t)dt$，其中 $u=g(x)$，$v=h(x)$
2. 根据链式法则：$\frac{dG}{dx}=\frac{\partial G}{\partial u}\frac{du}{dx}+\frac{\partial G}{\partial v}\frac{dv}{dx}$
3. 由微积分基本定理：$\frac{\partial G}{\partial u}=f(u)$，$\frac{\partial G}{\partial v}=-f(v)$
4. 因此：$\frac{dG}{dx}=f(g(x))g^{\prime }(x)-f(h(x))h^{\prime }(x)$

4.3 手动求解示例

设$F(x)={\int }_x^{x^2}tdt$，求 $F^{\prime }(x)$

根据复合变上限积分的求导公式： $$F^{\prime }(x)=f(g(x))\cdot g^{\prime }(x)-f(h(x))\cdot h^{\prime }(x)$$

1. 计算各部分：

   • $f(g(x))=f(x^2)=x^2$
   • $g^{\prime }(x)=2x$
   • $f(h(x))=f(x)=x$
   • $h^{\prime }(x)=1$

2. 代入公式： $$F^{\prime }(x)=(x^2)\cdot (2x)-(x)\cdot (1)=2x^3-x$$

所以，手动求解的结果是：$F^{\prime }(x)=2x^3-x$。

4.4 Python示例

import sympy as sp# 定义符号变量
x, t = sp.symbols('x t')
# 定义被积函数 f(t) = t
f = t
# 定义上下限函数
g = x**2  # 上限
h = x    # 下限
# 定义复合变上限积分
F = sp.integrate(f, (t, h, g))
# 求导
F_prime = sp.diff(F, x)
print("复合变上限积分的导数:", F_prime)

执行结果与手动求解结果一致，如下:

五、应用案例分析

5.1 基本求导问题

例1：计算 $\Phi (x)={\int }_2^x\frac{\sin t}{t}dt$ 的导数，并求 ${\Phi }^{\prime }(\frac{\pi }{2})$

手动求解：

• 由基本定理：${\Phi }^{\prime }(x)=\frac{\sin x}{x}$
• 代入 $x=\frac{\pi }{2}$：${\Phi }^{\prime }(\frac{\pi }{2})=\frac{\sin (\frac{\pi }{2})}{\frac{\pi }{2}}=\frac{2}{\pi }$

Python验证：

import sympy as sp
x = sp.symbols('x')
Phi_prime = sp.sin(x)/x
result = Phi_prime.subs(x, sp.pi/2)
print("Φ'(π/2) =", result)

执行结果与手动求解一致:

5.2 含参变量积分求导

例2：计算 $H(x)={\int }_0^x(x-t)\sin t^{2}dt$ 的二阶导数

手动求解：

1. 先展开：$H(x)=x{\int }_0^x\sin t^{2}dt-{\int }_0^{x}t\sin t^{2}dt$
2. 求一阶导数： $H^{\prime }(x)={\int }_0^x\sin t^{2}dt+x\sin x^2-x\sin x^2={\int }_0^x\sin t^{2}dt$
3. 求二阶导数：$H^{\prime \prime }(x)=\sin x^2$

Python验证：

import sympy as sp
x, t = sp.symbols('x t')
H = x*sp.integrate(sp.sin(t**2), (t, 0, x)) - sp.integrate(t*sp.sin(t**2), (t, 0, x))
H_double_prime = sp.diff(H, x, 2)
print("H''(x) =", sp.simplify(H_double_prime))

执行结果与手动求解一致:

5.3 极限计算中的应用

例3：求极限 ${\lim }_{x\to 0}\frac{{\int }_0^x\sin t^{2}dt}{x^2\sin x}$

手动求解：

1. 分析类型：当 $x\to 0$ 时，分子分母均趋于0，为$\frac{0}{0}$型未定式
2. 使用洛必达法则：
   • 分子导数：$\frac{d}{dx}{\int }_0^x\sin t^{2}dt=\sin x^2$
   • 分母导数：$\frac{d}{dx}(x^2\sin x)=2x\sin x+x^2\cos x$
3. 化简求极限： $$\underset{x\to 0}{\lim }\frac{\sin x^2}{2x\sin x+x^2\cos x}=\underset{x\to 0}{\lim }\frac{x^2}{2x\cdot x+x^2\cdot 1}=\frac{1}{3}$$

Python验证：

import sympy as sp
x, t = sp.symbols('x t')
numerator = sp.integrate(sp.sin(t**2), (t, 0, x))
denominator = x**2 * sp.sin(x)
limit_expr = numerator / denominator
result = sp.limit(limit_expr, x, 0)
print("极限值 =", sp.simplify(result))

执行结果:

5.4 函数性质分析

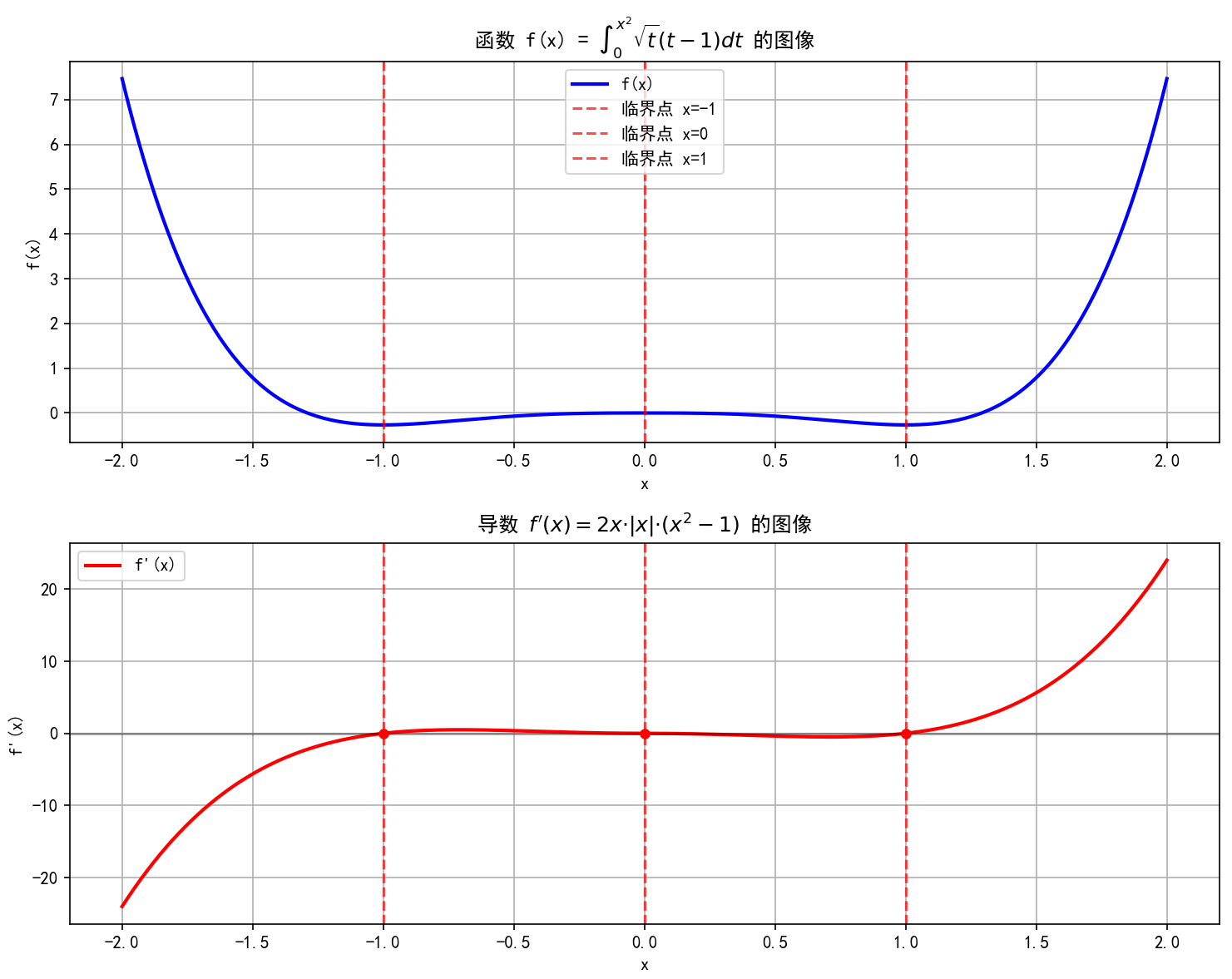
例4：分析函数 $f(x)={\int }_0^{x^2}\sqrt{t}(t-1)dt$ 的单调区间和极值点

手动求解：

1. 求导：$f^{\prime }(x)=2x\cdot |x|\cdot (x^2-1)$
2. 找临界点：令 $f^{\prime }(x)=0$，得 $x=-1,x=0,x=1$；
3. f(x) 与 $f^{\prime }(x)$ 的变化情况如下:

$x$	$(-\infty ,-1)$	$-1$	$(-1,0)$	$0$	$(0,1)$	$1$	$(1,+\infty )$
$f^{\prime }(x)$	-	0	+	0	-	0	+
$f(x)$	$\searrow$		$\nearrow$		$\searrow$		$\nearrow$

Python可视化：

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quadplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 定义被积函数
def integrand(t):return np.sqrt(t) * (t - 1)  # 正确对应 √t * (t-1)# 定义原函数 f(x) = ∫₀ˣ² √t (t-1) dt
def f(x):result, _ = quad(integrand, 0, x**2)return result# 定义导数函数 f'(x) = 2x * |x| * (x² - 1)（基于手动求解结果）
def f_prime(x):return 2 * x * np.abs(x) * (x**2 - 1)# 生成 x 值范围（覆盖临界点 -1, 0, 1）
x_vals = np.linspace(-2, 2, 500)
y_vals = [f(x) for x in x_vals]
dy_vals = [f_prime(x) for x in x_vals]  # 计算导数值# 创建图形和子图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))# 绘制函数图像
ax1.plot(x_vals, y_vals, 'b-', linewidth=2, label='f(x)')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')
ax1.set_title(r'函数 f(x) = $\int_{0}^{x^2}\sqrt{t}(t-1)dt$ 的图像') 
ax1.grid(True)
ax1.legend()# 标记临界点（导数为零的点）
critical_points = [-1, 0, 1]
for cp in critical_points:ax1.axvline(x=cp, color='red', linestyle='--', alpha=0.7, label=f'临界点 x={cp}')
ax1.legend()# 绘制导数图像
ax2.plot(x_vals, dy_vals, 'r-', linewidth=2, label="f'(x)")
ax2.axhline(y=0, color='k', linestyle='-', alpha=0.3)
ax2.set_xlabel('x')
ax2.set_ylabel("f'(x)")
ax2.set_title("导数 $f'(x) = 2x·|x|·(x^2-1)$ 的图像")
ax2.grid(True)
ax2.legend()# 标记导数零点
for cp in critical_points:ax2.axvline(x=cp, color='red', linestyle='--', alpha=0.7)ax2.plot(cp, 0, 'ro', markersize=5)  # 标记临界点plt.tight_layout()
plt.show()# 分析单调区间和极值点
print("=" * 50)
print("单调区间和极值点分析")
print("=" * 50)# 临界点
print(f"临界点: x = {critical_points}")# 测试各区间导数的符号
intervals = [(-np.inf, -1), (-1, 0), (0, 1), (1, np.inf)]
test_points = [-1.5, -0.5, 0.5, 1.5]  # 每个区间内的测试点print("\n单调性分析:")
for i, point in enumerate(test_points):deriv_val = f_prime(point)sign = "+" if deriv_val > 0 else "-" if deriv_val < 0 else "0"monotonicity = "递增" if deriv_val > 0 else "递减"print(f"  区间 {intervals[i]}: f'({point}) = {deriv_val:.2f} ({sign}) → 函数单调{monotonicity}")print("\n极值点分析:")
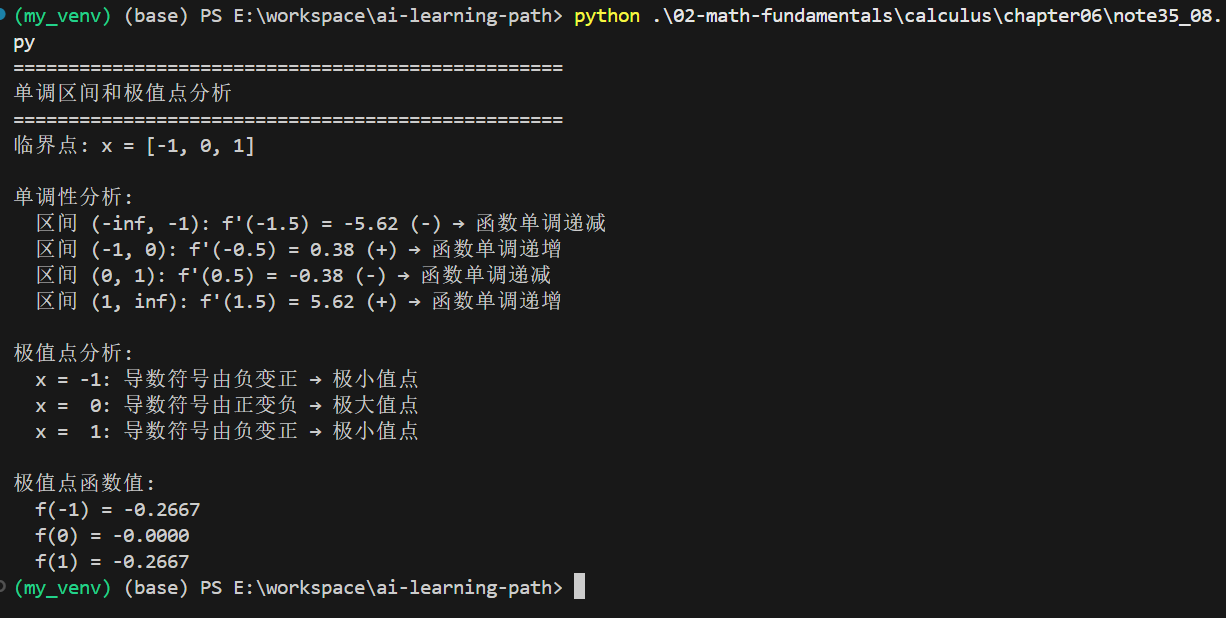
print("  x = -1: 导数符号由负变正 → 极小值点")
print("  x =  0: 导数符号由正变负 → 极大值点")
print("  x =  1: 导数符号由负变正 → 极小值点")# 验证临界点处的函数值
print("\n极值点函数值:")
for cp in critical_points:y_val = f(cp)print(f"  f({cp}) = {y_val:.4f}")

执行结果:

总结

变上限积分是微积分中连接微分与积分的关键概念，其核心在于微积分基本定理：连续函数的变上限积分是其原函数。这一结论不仅解决了定积分的计算问题，也揭示了微分与积分之间的互逆关系。

通过理论分析和Python实例验证，我们可以看到：

1. 变上限积分将积分运算转化为函数关系，使定积分计算可以通过求原函数来实现
2. 即使被积函数性质较差（如含有间断点），其变上限积分仍可能具有良好的性质（如连续性）
3. 复合变上限积分的求导法则为解决更复杂问题提供了工具

掌握变上限积分的概念和性质，对于深入理解微积分理论体系和解决实际问题都具有重要意义。

---

往期精彩回顾：

• 用Python来学微积分33-定积分的应用实例详解
• 用Python来学微积分34-定积分的基本性质及其应用

专栏导航目录 《程序员AI之路：从Python起步》完全学习导航

完整代码已开源 ai-learning-path，欢迎Star和Fork！

---

参考资料：

1. 扈志明《微积分》教材

互动邀请：如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题，欢迎在评论区分享交流！