李沐深度学习笔记D2-矩阵计算
求导数
导数就是一个切线的斜率,可以理解为一个曲线未来发展的趋向率
计算法则
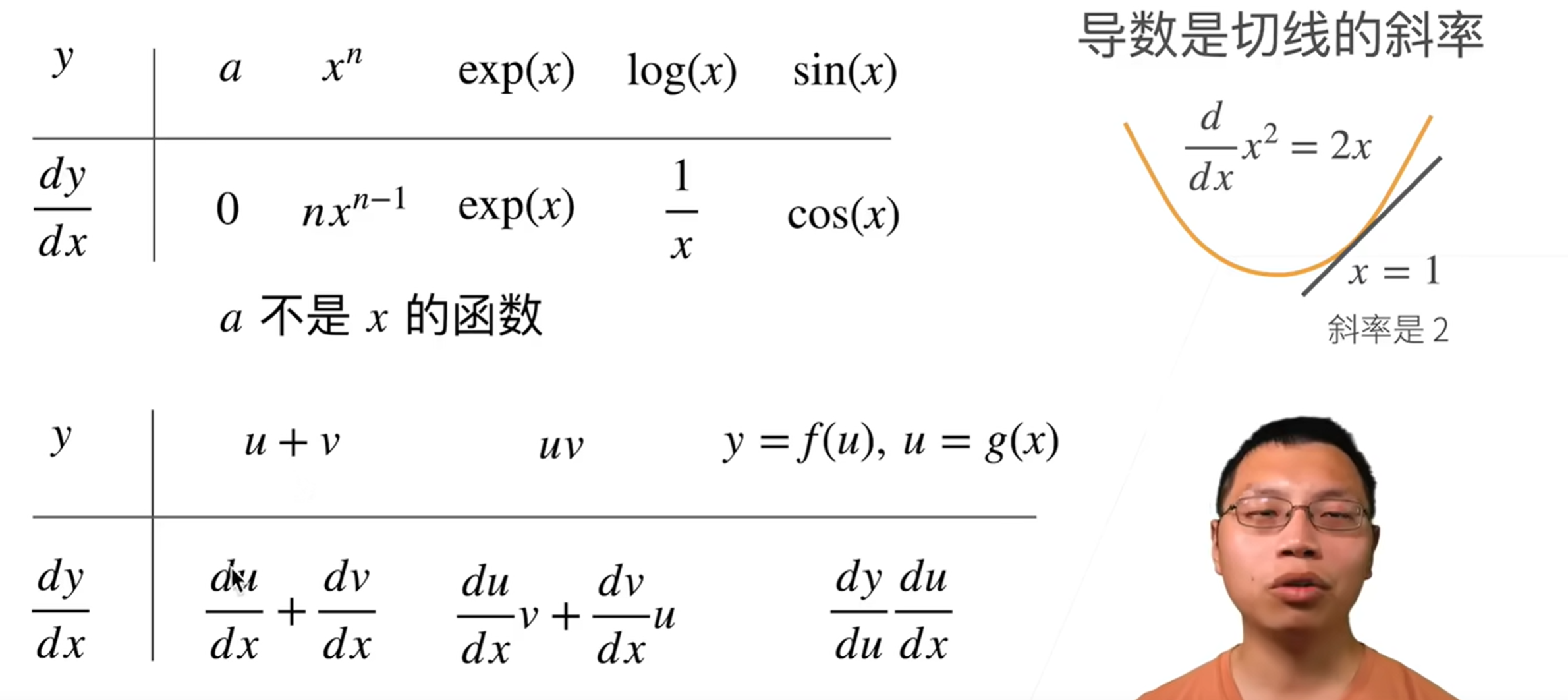
当切线的斜率有多个时,可以用亚导数求解,大概就是在某个范围某个值,某个范围内可以有多个值
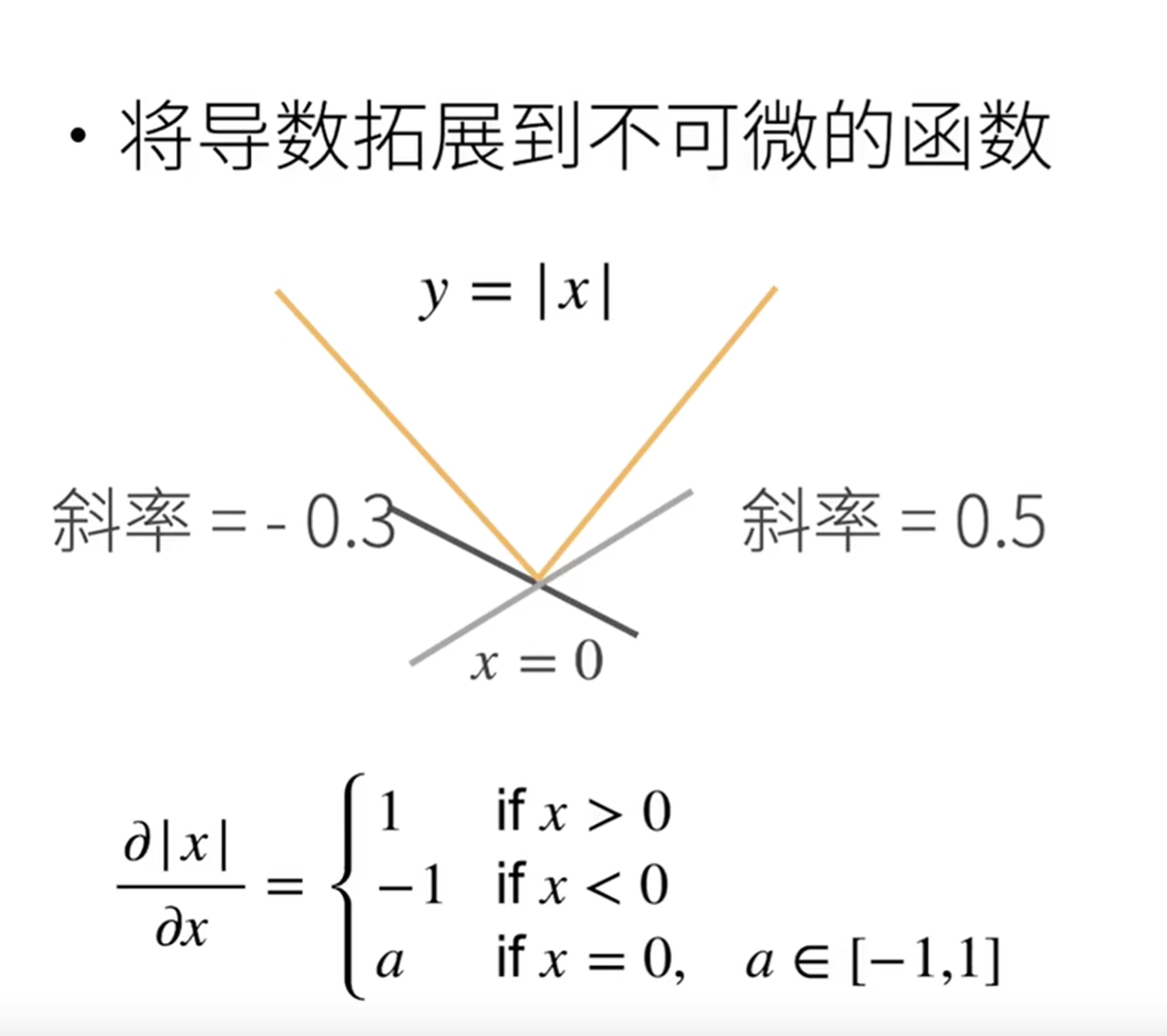
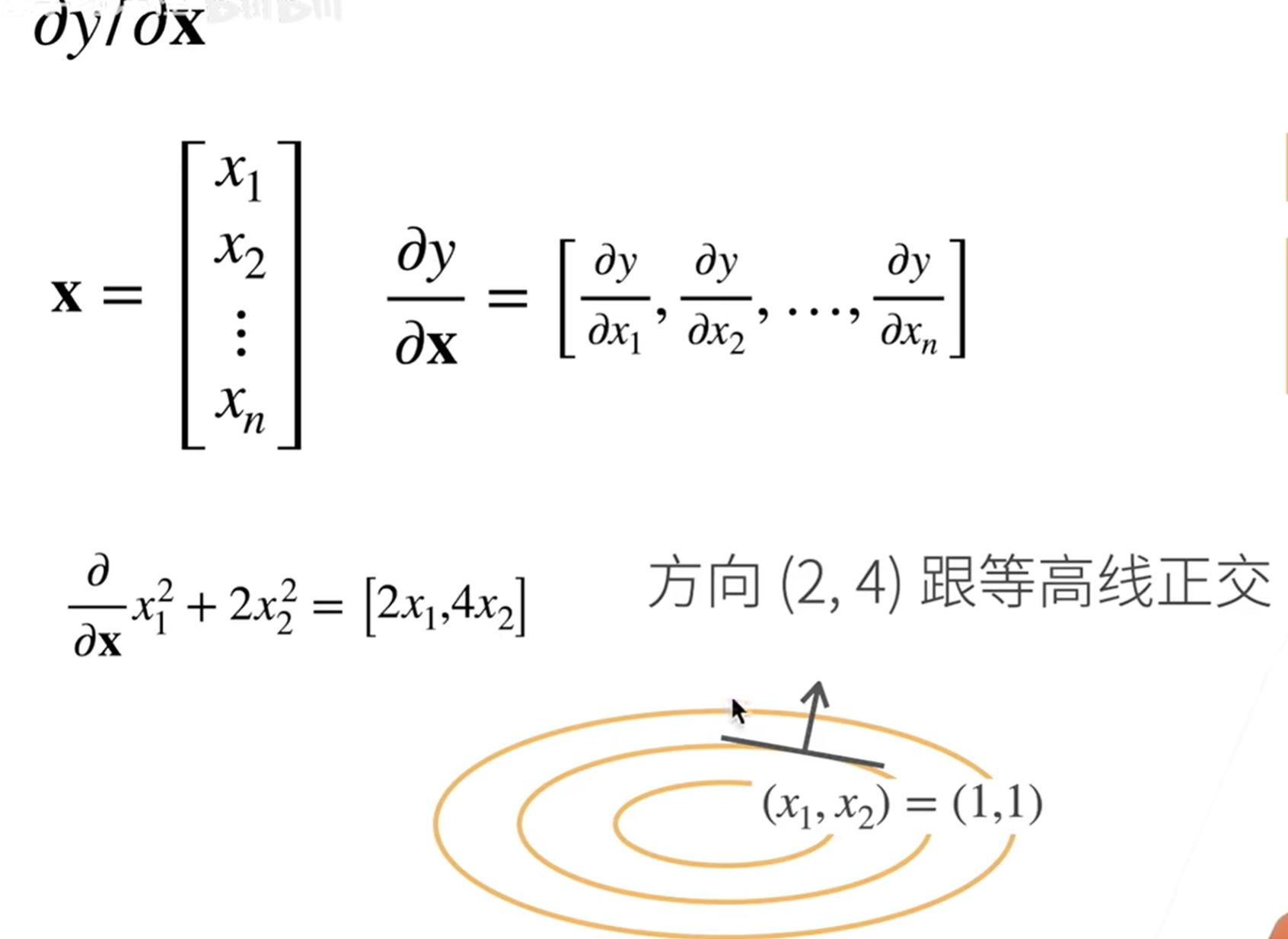
那么导数有什么用呢,导数既然可以理解成未来曲线发展的趋势,那么怎么和向量关联起来呢
这里讲到了一个梯度向量,代表的是一个离未来的趋势走向最远的那个指向,这里我也不知道未来会做什么用,但是确实是这个意思,未来应该是某个基础的理念
接着这里讲了求导的一些公式,比如一个常量a对x求导,因为a和x完全不相关,所以它对曲线的未来走向影响度为0,所以它的导数为0;如果是au,那么就是 a乘以u对x求导,这里的前提是u和x相关,如果也不相干,那么也是0;如果是 u + v,代表如果数据存在多个组成部分,就要估算每个组成部分对x的影响,然后计算出每个部分的求导,再求和算出整体的相关度,这就是 u + v 求导的结果是 u对x求导 + v对x求导;到这里逐渐开始明白了为什么需要导数。
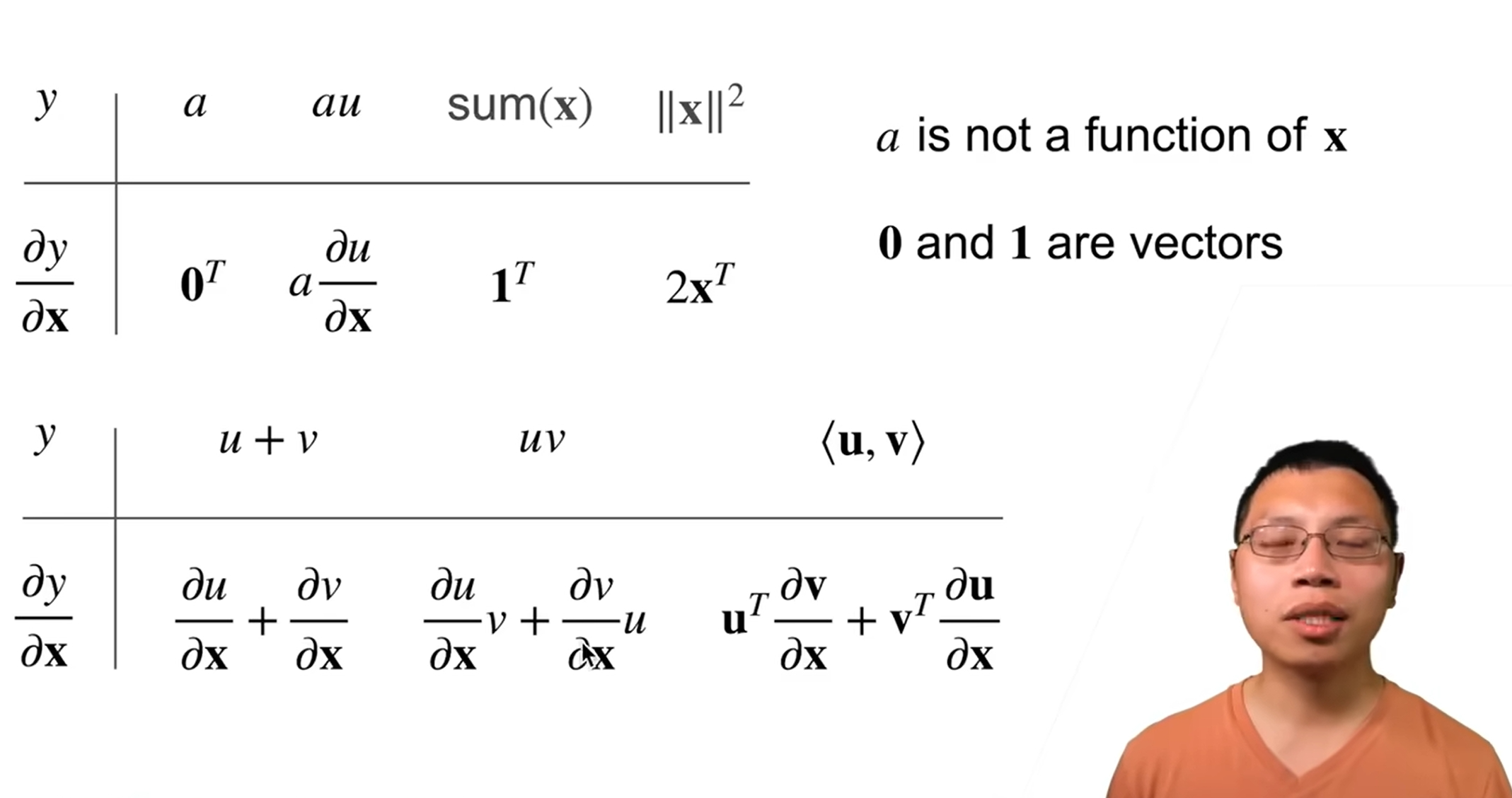
最后一个比较难理解的就是 <U, V> 的导数,这里指的是两个向量的导数,先说结论,两个向量的导数是一个矩阵
举例来说: y = f(x) 入参是一个变量x,出参是一个变量y,那么求导就是说一个变量x对输出变量y的影响
那么如果x和y都是一个向量呢,前面说了一个向量最直观的就是类似一个一维数组 x[x1,X2,X3…]
两个向量那么就类似于 结果集 y[y1,y2,y3 … yn] = a*x[x1,x2,…,xn] 这样的一个函数,每个y包括y1到yn都被x的所有向量影响,同理每个x也都被y向量的所有元素影响,那这样是不是就是一个矩阵
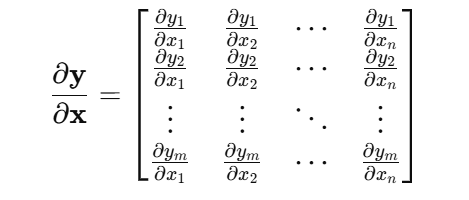
向量对向量的导数就是一个矩阵,这个矩阵叫雅可比矩阵
用相同的思想去理解,对于列向量关于标量的导数,比如y是一个向量x是一个标量(标量就是一个唯一值),y[y1,y2,…,yn] = a*x1,那么每个y都被唯一的x影响,那么这个列向量对于标量的导数,仍然是一个列向量,还是一个跟y列向量一样长的列向量
这个被称为分子布局,其实就是用某个布局的意义就在于你能控制你导数的形状,是标量还是向量还是矩阵,保证形状的一致可以方便进行运算,所以不仅有分子布局也有分母布局,两者是正好相反的,用哪个都可以
后面一节的视频是一个问题答疑视频
其中我记了一些我关注的问题
1, 导数为什么可以用来做梯度下降 ?
首先我用gpt5查了梯度的含义,梯度在这里可以指代为一个函数或者曲线上升最快的方向,比如一个曲线在上升,利用高中的知识,x轴偏移量非常小的情况下,y轴偏移量除以x轴偏移量应该可以用来当作导数也就是上升的趋势,那么梯度就是正好和上升的趋势的指向的向量成90度角分布的那个向量,也就是可以代表上升最快的那个趋势向量,如果想要延缓上升的趋势,那么我们就可以用梯度向量的正相反的趋势向量去发展这个函数,这就是梯度下降,可以有效的延缓上升的趋势
-
自动微分和计算图是什么?
查了gpt,了解到这都是计算的工具,也就是说其实我们的编程工具和框架中比如python/pytorch中,都有对应的函数可以帮助我们求导,不需要我们自己计算,但是了解其中的含义还是很必要的 -
什么是链式法则?
gpt给的定义是:如果一个函数由多个子函数复合嵌套组成,那么对这个函数求导,导数=外层函数的导数*内层函数的导数
举例:
标量的链式法则:
y=f(u) u=f(x) 那么y对x求导,导数=y对u求导 ✖ u对x求导
同理向量的链式法则:
(1)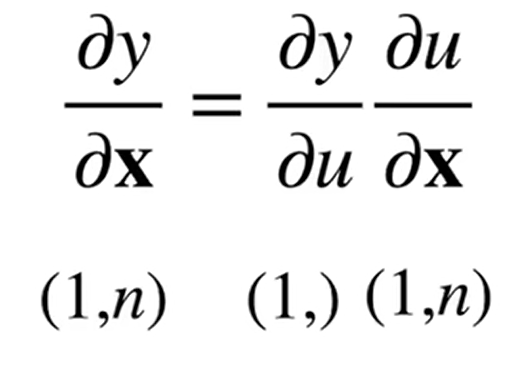
如上图,如果y是一个标量,u也是一个标量,x是一个向量
那么y对x求导,导数=y对u求导 ✖ u对x求导
此时,y标量对u标量求导,结果是一个标量
u标量对x向量求导,那么结果就是一个和x向量长度一样形状一样的向量
标量和向量相乘,结果还是一个和x形状相同的向量(2) 如果u是一个向量,y标量对u向量求导,导数形状与u相同为向量;u向量对x向量求导,导数为一个矩阵;向量乘以矩阵,(1,K) * (K,N) = (1*N) 之前学习的线性代数的思想
