外语教学网站开发广州计算机软件公司排名

摘要

这篇文章带你用 Swift 实战一道非常经典的 DFS + 记忆化搜索题目 —— LeetCode 329《矩阵中的最长递增路径》。看似一个简单的“走格子”游戏，实则考察了搜索顺序、剪枝策略和状态缓存等一系列算法技巧。我们将一步步分析这道题的解决过程，并附上可运行的 Swift 代码及详细注释。

描述

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

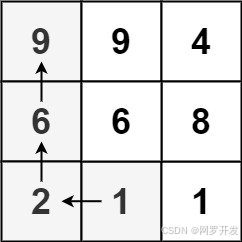
输入： matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出： 4 
解释： 最长递增路径为 [1, 2, 6, 9]。

示例 2：

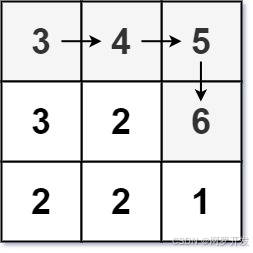
输入： matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出： 4 
解释： 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入： matrix = [[1]]
输出： 1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 231 - 1

题解答案

我们可以用 深度优先搜索（DFS）+ 记忆化搜索（Memoization） 来解决这个问题：

1. 对每个格子 (i, j) 进行 DFS，尝试向四个方向扩展路径；
2. 每当发现下一个格子数字更大，就继续递归搜索；
3. 为了避免重复计算，我们使用一个二维数组 cache[i][j] 存储每个格子的最长路径长度；
4. 所有格子的 DFS 跑一遍，返回最长的路径长度即可。

题解代码分析

import Foundationclass Solution {func longestIncreasingPath(_ matrix: [[Int]]) -> Int {guard !matrix.isEmpty else { return 0 }let m = matrix.countlet n = matrix[0].countvar cache = Array(repeating: Array(repeating: 0, count: n), count: m)let directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]func dfs(_ x: Int, _ y: Int) -> Int {if cache[x][y] != 0 {return cache[x][y]}var maxLength = 1for (dx, dy) in directions {let newX = x + dxlet newY = y + dyif newX >= 0, newX < m, newY >= 0, newY < n,matrix[newX][newY] > matrix[x][y] {maxLength = max(maxLength, dfs(newX, newY) + 1)}}cache[x][y] = maxLengthreturn maxLength}var result = 0for i in 0..<m {for j in 0..<n {result = max(result, dfs(i, j))}}return result}
}

代码解析

• cache[x][y]：用于记录格子 (x, y) 的最长路径长度，避免重复递归；
• dfs 是递归核心函数，它探索每一个可能的方向；
• directions 列出四个方向（上、下、左、右）；
• 最后遍历整个矩阵，取所有位置 DFS 的最大值作为结果。

示例测试及结果

我们可以写一个简单的测试模块，验证这个函数的效果：

let solution = Solution()let matrix1 = [[9, 9, 4],[6, 6, 8],[2, 1, 1]
]
print(solution.longestIncreasingPath(matrix1))  // 输出: 4let matrix2 = [[3, 4, 5],[3, 2, 6],[2, 2, 1]
]
print(solution.longestIncreasingPath(matrix2))  // 输出: 4let matrix3 = [[1]
]
print(solution.longestIncreasingPath(matrix3))  // 输出: 1

运行结果为：

4
4
1

可以看到，函数能准确输出矩阵中最长递增路径的长度。

时间复杂度

• O(m × n)：每个格子只会被访问一次，因为有缓存机制（记忆化搜索）。
• 对于矩阵中每个格子 (i, j)，我们最多做 4 次方向判断，但不会重复递归。

空间复杂度

• O(m × n)：我们使用了一个 cache 二维数组来保存每个格子的搜索结果；
• 递归栈的深度最坏为 m × n，不过大部分情况下都远小于这个上限。

总结

这道题看起来像暴力 DFS，但只要引入记忆化搜索（Memoization），效率就大幅提升，避免了重复计算。也体现了典型的“搜索+缓存”优化套路。

如果你在刷题中遇到「在图中找最长路径」的问题，不妨第一时间考虑：

• 是否可以 DFS 解决？
• 子问题结果能不能缓存？

这个技巧在图搜索、DP、树结构中经常用到，是刷题的通关利器。