当前位置：首页 > news >正文

基于LQR和PID控制算法的一级倒立摆MATLAB实现

news 2025/11/6 11:48:49

一、系统建模与参数设置

1. 状态空间模型

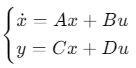
请添加图片描述

其中状态变量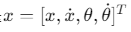请添加图片描述

2. 参数定义

% 物理参数
M = 1.096;    % 小车质量 (kg)
m = 0.109;    % 摆杆质量 (kg)
l = 0.25;     % 摆长 (m)
g = 9.8;      % 重力加速度 (m/s²)
b = 0.1;      % 摩擦系数
I = 0.0034;   % 摆杆转动惯量 (kg·m²)% 状态空间矩阵
A = [0 1 0 0;0 -(I+m*l²)*b/(I*(M+m)+M*m*l²) m²*g*l²/(I*(M+m)+M*m*l²) 0;0 0 0 1;0 -m*b*l/(I*(M+m)+M*m*l²) m*g*l*(M+m)/(I*(M+m)+M*m*l²) 0];
B = [0; (I+m*l²)/(I*(M+m)+M*m*l²); 0; -m*l/(I*(M+m)+M*m*l²)];
C = eye(4);
D = zeros(4,1);

二、LQR控制器设计

1. 权重矩阵选择

Q = diag([1000, 0, 200, 0]);  % 状态权重
R = 1;                        % 控制输入权重

2. LQR增益计算

[K, P, E] = lqr(A, B, Q, R);

3. 闭环系统仿真

% 初始状态 [x, x_dot, theta, theta_dot]
x0 = [0.1; 0; 0.1; 0]; % 闭环系统矩阵
A_cl = A - B*K;
sys_cl = ss(A_cl, B, C, D);% 仿真参数
t = 0:0.01:5;
u = 0.1*ones(size(t));  % 阶跃输入% 仿真
[y, t] = lsim(sys_cl, u, t, x0);% 绘图
figure;
subplot(2,1,1);
plot(t, y(:,1), 'r', t, y(:,3), 'b');
xlabel('时间 (s)');
ylabel('位置 (m)/角度 (rad)');
legend('小车位置', '摆杆角度');
title('LQR控制响应');subplot(2,1,2);
stem(t, u*1000);
xlabel('时间 (s)');
ylabel('控制输入 (mN)');
title('LQR控制量');

三、PID控制器设计

1. 参数整定

Kp = 50;    % 比例系数
Ki = 10;    % 积分系数
Kd = 10;    % 微分系数% PID控制器
pid = pid(Kp, Ki, Kd);

2. 闭环系统实现

% 闭环系统矩阵
A_pid = A - B*pid.C;
sys_pid = ss(A_pid, B, C, D);% 仿真
[y_pid, t_pid] = lsim(sys_pid, u, t, x0);% 绘图对比
figure;
subplot(2,1,1);
plot(t, y(:,1), 'r', t_pid, y_pid(:,1), 'b--');
hold on;
plot(t, y(:,3), 'g', t_pid, y_pid(:,3), 'm--');
legend('LQR位置', 'PID位置', 'LQR角度', 'PID角度');
title('PID与LQR控制对比');subplot(2,1,2);
plot(t, u*1000, 'r', t_pid, pid.out*1000, 'b--');
xlabel('时间 (s)');
ylabel('控制输入 (mN)');
legend('LQR控制量', 'PID控制量');

四、完整m文件代码

%% 一级倒立摆控制仿真
clear; clc;%% 系统参数
M = 1.096; m = 0.109; l = 0.25; g = 9.8; b = 0.1; I = 0.0034;% 状态空间模型
A = [0 1 0 0;0 -(I+m*l²)*b/(I*(M+m)+M*m*l²) m²*g*l²/(I*(M+m)+M*m*l²) 0;0 0 0 1;0 -m*b*l/(I*(M+m)+M*m*l²) m*g*l*(M+m)/(I*(M+m)+M*m*l²) 0];
B = [0; (I+m*l²)/(I*(M+m)+M*m*l²); 0; -m*l/(I*(M+m)+M*m*l²)];
C = eye(4); D = zeros(4,1);%% LQR控制
Q = diag([1000, 0, 200, 0]); R = 1;
[K, P, E] = lqr(A, B, Q, R);
A_cl = A - B*K;
sys_cl = ss(A_cl, B, C, D);%% PID控制
Kp = 50; Ki = 10; Kd = 10;
pid = pid(Kp, Ki, Kd);
A_pid = A - B*pid.C;
sys_pid = ss(A_pid, B, C, D);%% 仿真
t = 0:0.01:5;
u = 0.1*ones(size(t));
x0 = [0.1; 0; 0.1; 0];% LQR仿真
[y_lqr, t_lqr] = lsim(sys_cl, u, t, x0);% PID仿真
[y_pid, t_pid] = lsim(sys_pid, u, t, x0);%% 结果可视化
figure;
subplot(2,1,1);
plot(t_lqr, y_lqr(:,1), 'r', t_pid, y_pid(:,1), 'b--');
hold on;
plot(t_lqr, y_lqr(:,3), 'g', t_pid, y_pid(:,3), 'm--');
xlabel('时间 (s)');
ylabel('位置 (m)/角度 (rad)');
legend('LQR位置', 'PID位置', 'LQR角度', 'PID角度');subplot(2,1,2);
stem(t_lqr, u*1000, 'r', t_pid, pid.out*1000, 'b--');
xlabel('时间 (s)');
ylabel('控制输入 (mN)');
legend('LQR控制量', 'PID控制量');