《P2585 [ZJOI2006] 三色二叉树》
题目描述
一棵二叉树可以按照如下规则表示成一个由 0、1、2 组成的字符序列,我们称之为“二叉树序列 S”:
S=⎩⎨⎧01S12S1S2表示该树没有子节点表示该树有一个节点,S1为其子树的二叉树序列表示该树有两个子节点,S1和S2分别表示其两个子树的二叉树序列
例如,下图所表示的二叉树可以用二叉树序列 S=21200110 来表示。
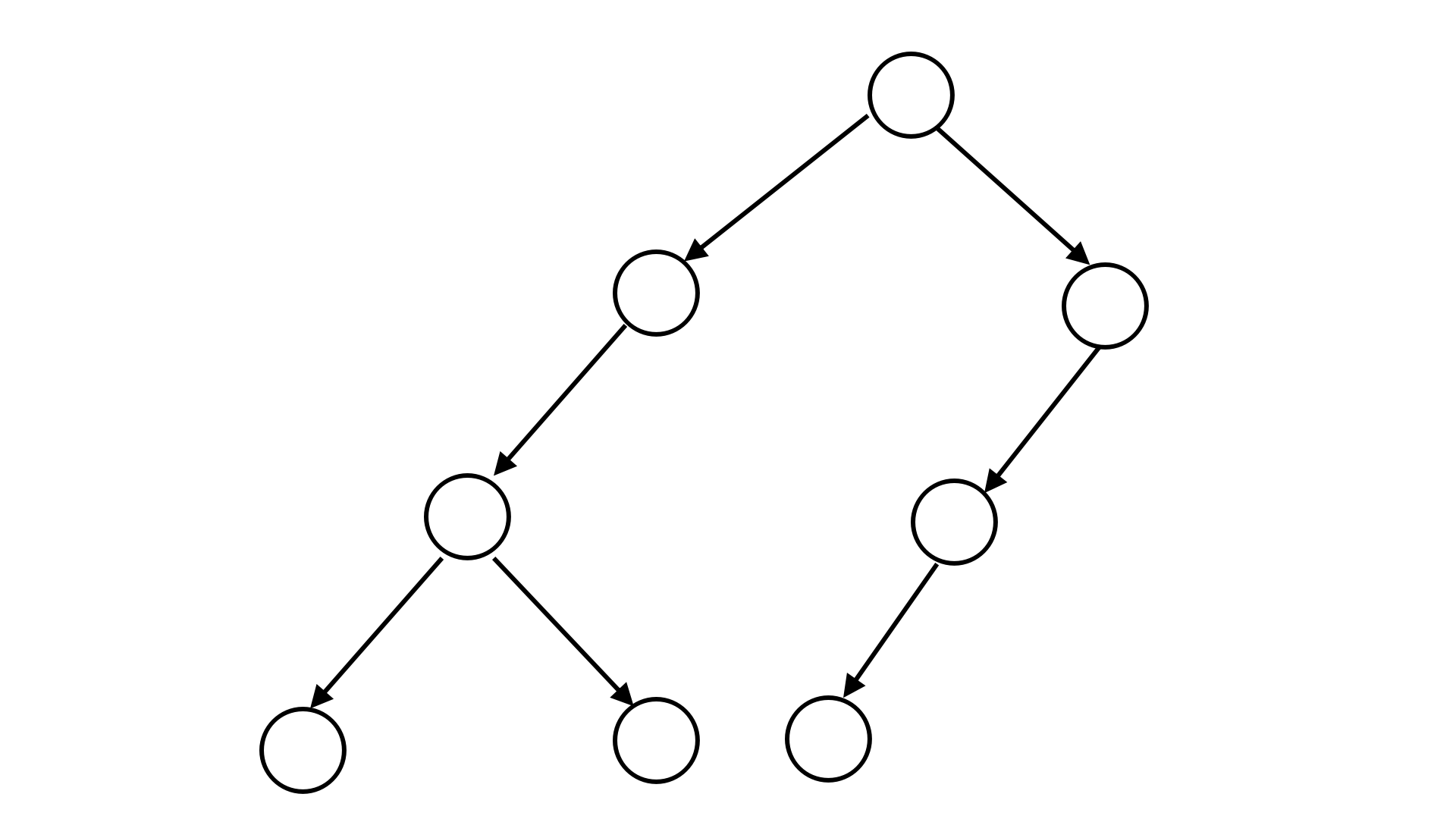
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 s,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
输入输出样例
输入 #1复制
1122002010
输出 #1复制
5 2
说明/提示
数据规模与约定
对于全部的测试点,保证 1≤∣s∣≤5×105,s 中只含字符 0 1 2。
代码实现:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;const int n=0,r=1,y=2,w=3;struct nd{int c[3];};nd t[500101];
int mx[500101][4],mn[500101][4];
char s[500101];
int it=0;void dp(int x){mx[x][r]=0;mx[x][y]=0;mx[x][w]=1;mn[x][r]=0;mn[x][y]=0;mn[x][w]=1;for(int i=1;i<=2;i++)if(t[x].c[i])dp(t[x].c[i]);int l=t[x].c[1],rc=t[x].c[2];mx[x][w]+=max(mx[l][r]+mx[rc][y],mx[rc][r]+mx[l][y]);mx[x][r]+=max(mx[l][w]+mx[rc][y],mx[rc][w]+mx[l][y]);mx[x][y]+=max(mx[l][w]+mx[rc][r],mx[rc][w]+mx[l][r]);mn[x][w]+=min(mn[l][r]+mn[rc][y],mn[rc][r]+mn[l][y]);mn[x][r]+=min(mn[l][w]+mn[rc][y],mn[rc][w]+mn[l][y]);mn[x][y]+=min(mn[l][w]+mn[rc][r],mn[rc][w]+mn[l][r]);
}void mk(){int tmp=++it;if(s[tmp]=='1'){t[tmp].c[1]=it+1;mk();return;}if(s[tmp]=='2'){t[tmp].c[1]=it+1;mk();t[tmp].c[2]=it+1;mk();return;}
}int main(){scanf("%s",s+1);mk();dp(1);printf("%d ",max(max(mx[1][r],mx[1][y]),mx[1][w]));printf("%d ",min(min(mn[1][r],mn[1][y]),mn[1][w]));return 0;
}