力扣.84柱状图中最大矩形 力扣.134加油站牛客.abb（hard 动态规划+哈希表)牛客.哈夫曼编码

目录

力扣.84柱状图中最大矩形 

力扣.134加油站

牛客.abb（hard 动态规划+哈希表)

牛客.哈夫曼编码

---

力扣.84柱状图中最大矩形 

1.暴力解法如同那个中心拓展算法一样，把每一个点作为中心向外扩展最大面积，超时

class Solution {public int largestRectangleArea(int[] heights) {int n=heights.length;//中心拓展方法int sum=0;Stack<Integer>s=new Stack<>();for(int i=0;i<n;i++){int count=1;int left=i-1;int right=i+1;while(left>=0&&s.peek()=heights[i]){left--;count++;}while(right<n&&s.peek()>=heights[i]){right++;count++;}sum=Math.max(sum,heights[i]*count);}return sum;}
}

下面的优化，我说实话我都要有点没看懂，就是他的有时候思维并非像是人类一样，能直接往后看看到多少多少，而是她更像是怎么说，像是一个机器的思维，就是当前状态结果这个不是正确的，就比如2，5，6，6，6，2，1 ，我们人是从第一个6开始，就想着到最后面的6，他的机器是可能第二个6，第3个6才出来正确结果，因此，这是我说的机器和人思维不同的一些地方。

class Solution {public int largestRectangleArea(int[] heights) {int n = heights.length;Deque<Integer> st = new ArrayDeque<>();st.push(-1); // 在栈中只有一个数的时候，栈顶的「下面那个数」是 -1，对应 left[i] = -1 的情况,表示他的右边界-左边界值int ans = 0;for (int right = 0; right <= n; right++) {int h = right < n ? heights[right] : -1;while (st.size() > 1 && h <= heights[st.peek()]) {int i = st.pop(); // 矩形的高（的下标）int left = st.peek(); // 栈顶下面那个数就是 leftans = Math.max(ans, heights[i] * (right - left - 1));}st.push(right);}return ans;
}
}

力扣.134加油站

他的难点，第一个就是暴力时候，这么表示环，使用 [(i+step)%n]就好，然后肯定是要走xxx步

然后贪心的第二个点，假如出现负数，也就是小于0的情况

假如从0为起点开始，从0 走到4是负数了，那么1，2，3也没必要走，当然，是在0为负数的情况

当然，假如你想要从0走到1，那么0一定大于0.。依次类推。

public int canCompleteCircuit(int[] gas, int[] cost) {int n=gas.length;       //仅考虑从加油站的净收益即可 int[]dif=new int[n];int sum=0;for(int i=0;i<n;i++){dif[i]=gas[i]-cost[i];}//从不同起点出发for(int i=0;i<n;i++){int count=0;//假如使用一个变量step表示当前走了多少步int step=0;for( ;step<n;step++){//每次的差值count+=dif[(i+step)%n];//假如道路中间变成负数，就无法到达if(count<0){i=i+step;break;}}if(count>=0)return i;}return -1;}

牛客.abb（hard 动态规划+哈希表)

像是动态规划，a,b点-结合一个子序列

以i为结尾的所有的子序列

 public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();String aa=in.next();char[]a=aa.toCharArray();int []f=new int[26];int []g=new int[26];int []dp=new int[26];long sum=0;for(int i=0;i<n;i++){int x=a[i]-'a';dp[x]=f[x];sum+=dp[x];f[x]=f[x]+i-g[x];g[x]=g[x]+1;}System.out.print(sum);}

牛客.哈夫曼编码

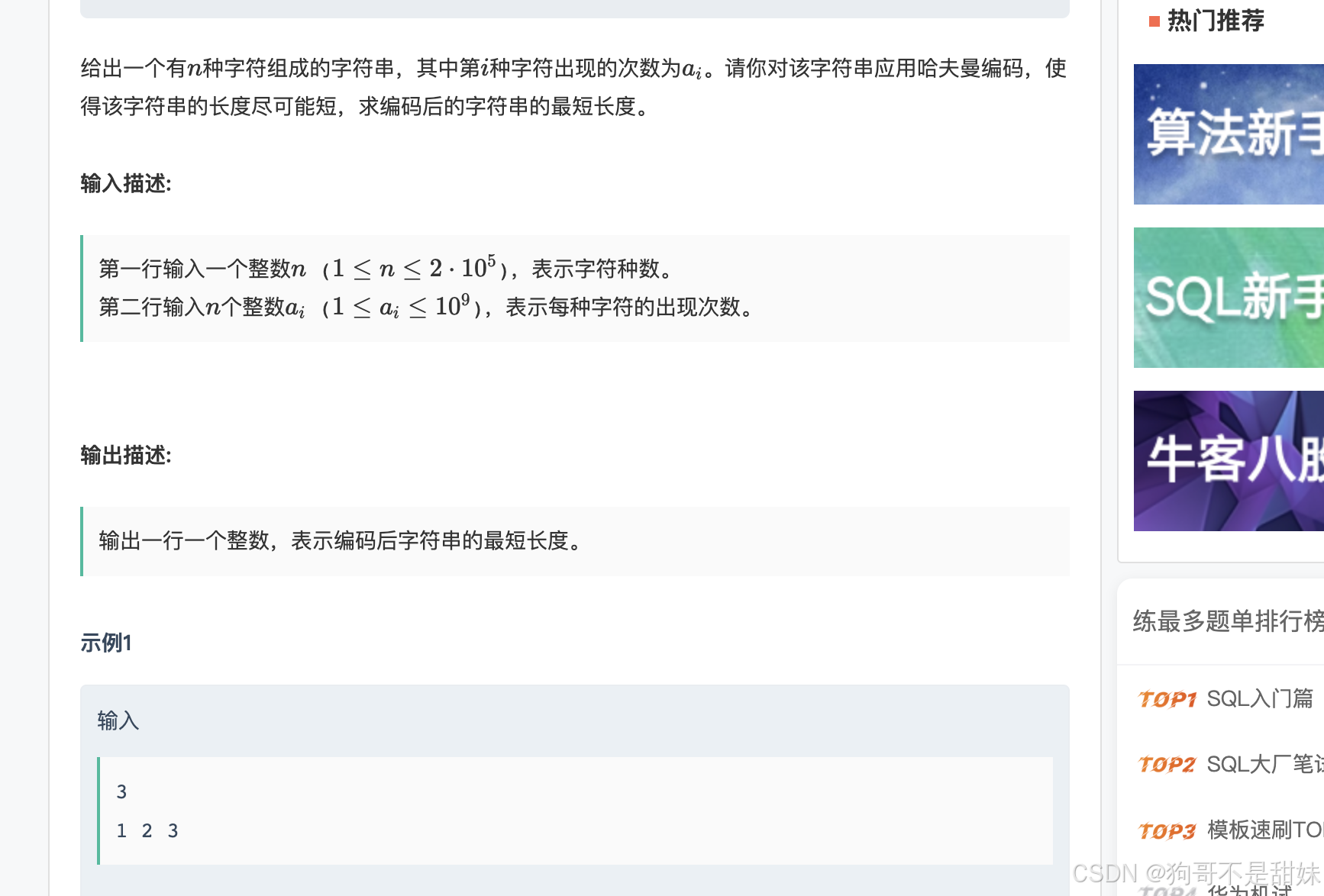
什么是哈夫曼编码

压缩存储

abbcccdd 二进制。使用二进制来存储，先对出现的字符进行编码

比如

a:0

b:01

c:001

d:11

那么长长的字符串由字符串表示的话，就可以非常省空间，但是会出现问题，就像是滑动窗口的漏包     比如001   : ab 或者c，这样就有歧义了，说明这种编码是不合理的，即错误的

压缩的目的是省空间，当前这个c出现三次，那么c的字符应该短一些，这样他就省空间

哈夫曼编码是最优的压缩存储方式

怎么用？

1.统计每个字符的频次

2.根据频次构建最优二叉树

3.根据最优二叉树编码

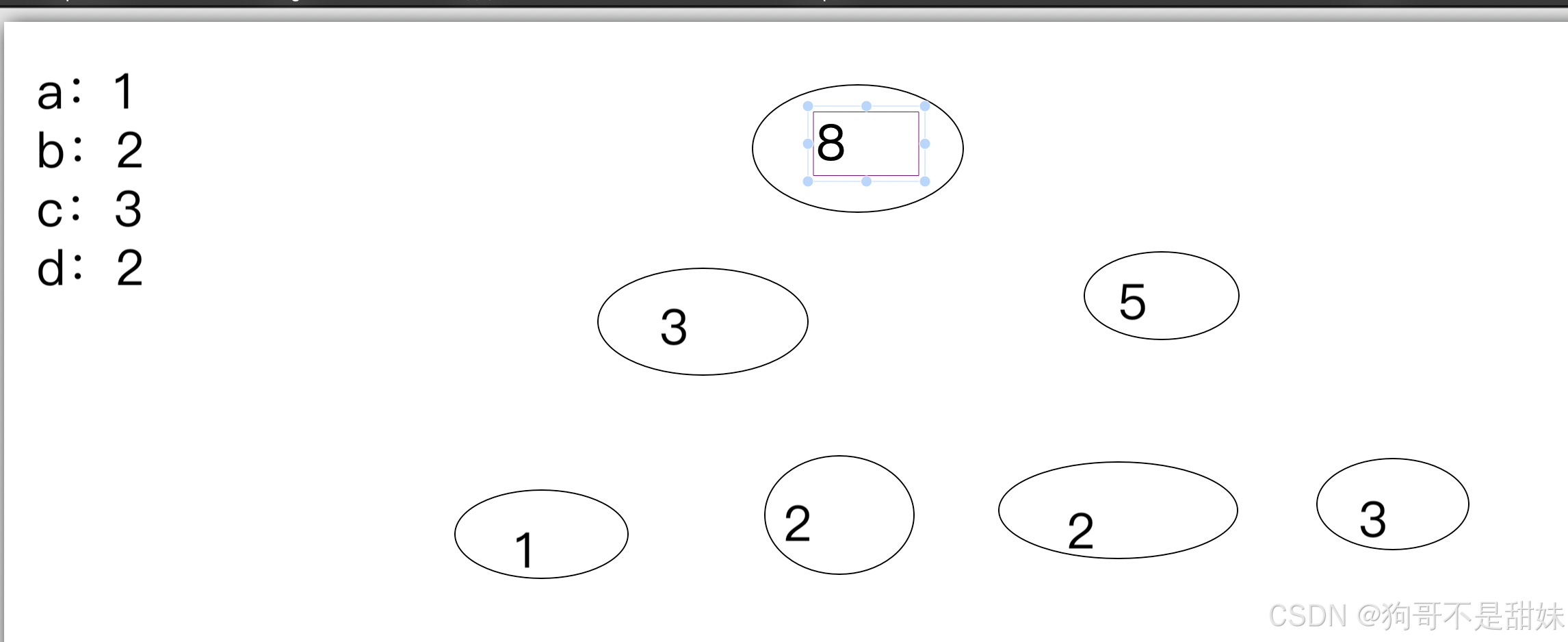
a:1

b:2

c:3

d:2

此时有一个大圆圈 频次为1的，为2的两个，为3的一个，每次从集合中取出权值最小的两个，由两个最小的，再去一个一个构建。

总结就是每次取两个小的，然后相加，再去插入以此类推。

  public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();PriorityQueue<Long>q=new PriorityQueue<>();for(int i=0;i<n;i++){q.add(in.nextLong());}long sum=0;while(q.size()>1){long x=q.poll();long y=q.poll();q.add(x+y);sum+=x+y;}System.out.print(sum);}