Voronoi 图及其在路径搜索中的应用

Voronoi 图及其在路径搜索中的应用

1. Voronoi 图的基本概念

Voronoi 图（Voronoi Diagram），又称泰森多边形（Thiessen Polygon）、Dirichlet Tessellation，是一种根据距离度量将平面空间划分为若干个区域的方法。

给定平面上的一组离散点集
P={p1,p2,…,pn} P = \{p_1, p_2, \dots, p_n\} P={p1​,p2​,…,pn​}
对于空间中任一位置 $x$，令 $\text{dist}(x,p_i)$ 表示从 $x$ 到点 $p_i$ 的距离（常用欧氏距离）。
Voronoi 区域 $V(p_i)$ 定义为：
V(pi)={x∣dist(x,pi)≤dist(x,pj),∀j≠i} V(p_i) = \{ x \mid \text{dist}(x, p_i) \le \text{dist}(x, p_j), \forall j\neq i \} V(pi​)={x∣dist(x,pi​)≤dist(x,pj​),∀j=i}

换句话说，Voronoi 图将整个空间划分成 $n$ 个区域，每个区域的所有点距离所属生成点最近。

2. 数学性质与特征

• 多边形结构：在二维欧氏空间中，Voronoi 区域是由线段和射线围成的凸多边形。
• 边界位置：边界是两生成点距离相等的所有位置的集合，即以两点为焦点的垂直平分线。
• 对偶关系：Voronoi 图的对偶图是德劳内三角剖分（Delaunay Triangulation），这使得在建模和算法实现上非常方便。

3. 构建算法

常见的构建方法包括：

1. 直接几何法：穷举两点的垂直平分线，计算多边形交集（适用于小规模点集）。
2. 扫描线算法：如 Fortune’s Algorithm，复杂度可达到 $O(n\log n)$。
3. 基于 Delaunay 三角化：先求 Delaunay 三角剖分，再利用对偶关系生成 Voronoi 图。

4. Voronoi 图在路径搜索中的作用

Voronoi 图在路径规划和搜索领域非常有用，尤其适用于机器人导航、自动驾驶、地图分析等场景。应用价值主要体现为：

4.1 保持最大安全距离

在机器人导航中，如果障碍物或危险点视为生成点，通过构建 Voronoi 图，可以得到一个骨架网络（Voronoi 边）。这个骨架的位置通常远离障碍物，能保证机器人运动时与障碍物保持最大化的最小距离，提高安全性。

4.2 构造导航图

构建 Voronoi 图后，边界可以形成一组稀疏且连通的路径网络。路径规划可在该网络上进行，而不是在整个连续空间中搜索，减少了搜索空间和计算量。

4.3 与搜索算法结合

Voronoi 图可与常见搜索算法结合：

• A* 或 Dijkstra：在 Voronoi 图的边构成的网络上运行，快速获取全局最优路径。
• Probabilistic Roadmap (PRM) & RRT：Voronoi 边为采样提供安全参考，提高路径的可行性和稳定性。

4.4 应对动态场景

在动态环境中（如人群移动或车辆流动），可以根据目标和障碍的位置实时更新 Voronoi 网络，并重新进行路径搜索，适用于实时决策系统。

5. 应用实例（机器人路径规划）

场景：在一个平面地图中，多个障碍物作为生成点。
步骤：

1. 输入数据：障碍物的位置坐标。
2. 生成 Voronoi 图：计算边界与骨架结构。
3. 建立图结构：将 Voronoi 边转化为节点与边的图。
4. 运行搜索算法：在该图上用 A* 搜索起点到终点的最短路径。
5. 输出路径：结果路径在空间上尽量远离障碍物，并能高效抵达终点。

此方法的优势：

• 安全距离最大化。
• 路径平滑且可预测。
• 可以与代价地图结合，进一步优化路径质量。

6. 总结

Voronoi 图通过距离度量自然地将空间划分为多个区域，它的骨架结构在路径规划中能提供安全、稀疏且高效的导航网络。结合图搜索算法与动态更新机制，Voronoi 图不仅适用于静态地图的最短路径规划，还能满足实时变化环境中的快速导航需求。

7. 示例及代码

import numpy as np
import matplotlib as mpl
mpl.get_cachedir()
import matplotlib.pyplot as plt
from scipy.spatial import Voronoi, voronoi_plot_2d
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False# 随机生成一些点（可代表障碍物或参考点）
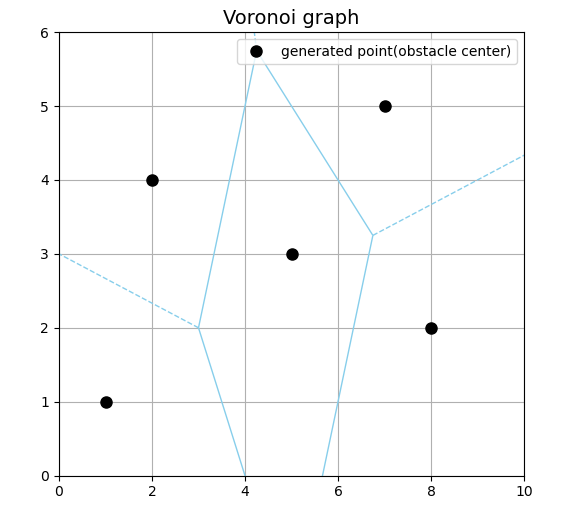
points = np.array([[1, 1], [2, 4], [5, 3], [7, 5], [8, 2]])# 计算 Voronoi 图
vor = Voronoi(points)# 绘制 Voronoi 图
fig, ax = plt.subplots(figsize=(6, 6))
voronoi_plot_2d(vor, ax=ax, show_points=True, show_vertices=False, line_colors="skyblue"
)# 绘制障碍物点
ax.plot(points[:, 0], points[:, 1], "ko", markersize=8, label="generated point(obstacle center)"
)# # 模拟路径搜索的结果（在骨架上选一条路径）
# # 这里用一条简化的路径作示意
# path = np.array([[0.5, 0.5], [2, 2], [4, 3], [6, 4], [9, 3]])
# ax.plot(path[:, 0], path[:, 1], "r-", linewidth=2, label="path search result")# 格式设置
ax.set_xlim(0, 10)
ax.set_ylim(0, 6)
ax.set_title("Voronoi graph", fontsize=14)
ax.legend()
ax.grid(True)plt.show()